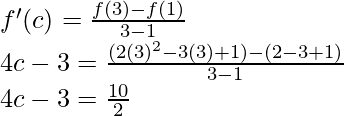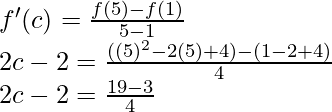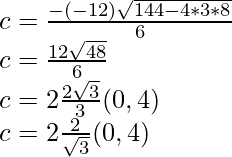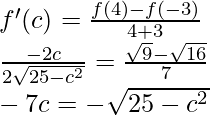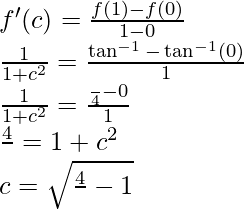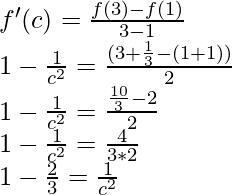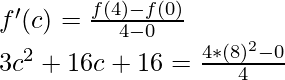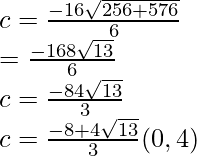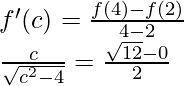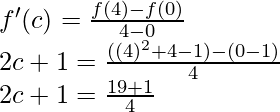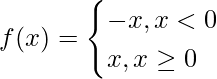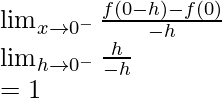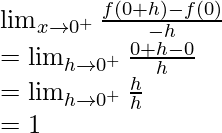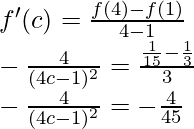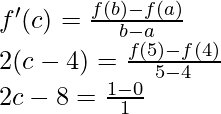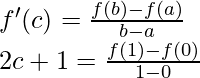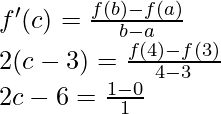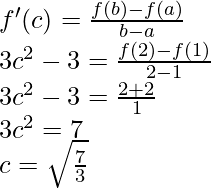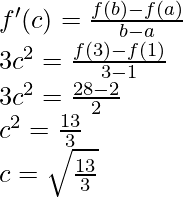Pregunta 1 (i). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 2 – 1 en [2, 3]
Solución:
Dado que
f(x) = x2 – 1
Dado que la f(x) = x 2 – 1 dada es una función polinomial.
Entonces, la f(x) dada es continua en [2, 3] y derivable en (2, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (2, 3) tal que,
2c = (8 – 3)
c = 5/2 ∈ (2, 3)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (ii). Verifique el teorema del valor medio de Lagrange para lo siguiente en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 3 – 2x 2 – x + 3 en [0, 1].
Solución:
Dado que
f(x) = x 3 – 2x 2 – x + 3
Dado que la f(x) = x 3 – 2x 2 – x + 3 dada es una función polinomial.
Entonces, la f(x) dada es continua en [0, 1] y diferenciable en (0, 1)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 1) tal que,
3c 2 – 4ac – 1 = 1 – 3
3c 2 – 4c + 1 = 0
3c 2 – 3c – c + 1 = 0
3c(c – 1) – 1(c – 1) = 0
(3c – 1)(c – 1) = 0
c = 1/3 ∈ (0, 1)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (iii). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x(x – 1) en [1, 2].
Solución:
Dado que
f(x) = x(x – 1) ⇒ x 2 – x
Dado que f(x) = x 2 – x es una función polinomial.
Entonces, la f(x) dada es continua en [1, 2] y derivable en (1, 2)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 2) tal que,
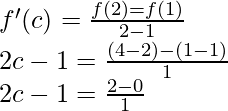
2c = 3
c = 3/2 ∈ (1, 2)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (iv). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 2 – 3x + 2 en [-1, 2].
Solución:
Dado que
f(x) = x2 – 3x + 2
Dado que la f(x) = x 2 – 3x + 2 dada es una función polinomial.
Entonces, la f(x) dada es continua en [-1, 2] y derivable en (-1, 2)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (-1, 2) tal que,
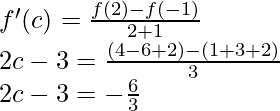
2c – 3 = -2
2c = 1
c = 1/2 ∈ (-1, 2)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (v). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = 2x 2 – 3x + 1 en [1, 3].
Solución:
Dado que,
f(x) = 2x 2 – 3x + 1
Dado que f(x) = 2x 2 – 3x + 1 es una función polinomial.
Entonces, la f(x) dada es continua en [1, 3] y derivable en (1, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 3) tal que,
4c – 3 = 5
4c = 5 + 3
4c = 8
c = 2 ∈ (1, 3)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (vi). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada caso, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 2 – 2x + 4 en [1, 5].
Solución:
Dado que,
f(x) = x2 – 2x + 4
Dado que la f(x) = x 2 – 2x + 4 dada es una función polinomial.
Entonces, la f(x) dada es continua en [1, 5] y derivable en (1, 5)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 5) tal que,
2c – 2 = 16/4
2c – 2 = 4
2c = 6
c = 3 ∈ (1, 5)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (vii). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = 2x – x 2 en [0, 1].
Solución:
Dado que,
f(x) = 2x – x 2
Dado que la f(x) = 2x – x 2 dada es una función polinomial.
Entonces, la f(x) dada es continua en [0, 1] y diferenciable en (0, 1)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 1) tal que,
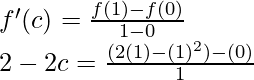
2 – 2c = 1
1 = 2c
c = 1/2 ∈ (0, 1)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (viii). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como lo establece el teorema del valor medio de Lagrange f(x) = (x – 1)(x – 2)(x – 3) en [0, 4].
Solución:
Dado que,
f(x) = (x – 1)(x – 2)(x – 3)
Dado que la función f(x) = (x – 1)(x – 2)(x – 3) es una función polinomial.
Entonces, la f(x) dada es continua en [0, 4] y diferenciable en (0, 4)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 4) tal que,
(c – 1)(c – 2) + (c – 2)(c – 3) + (c – 1)(c – 3)
do 2 – 3c + 2 + do 2 + 5c + 6 + do 2 – 4c + 3
3c 2 – 12c + 11 = 3
3c 2 = 12c + 8 = 0
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (ix). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como lo establece el teorema del valor medio de Lagrange f(x) 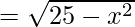 en [-3, 4].
en [-3, 4].
Solución:
Dado que,
f(x)
La f(x) dada existe, si
25 – x2 ≥ 0
× 2 ≤ 25
x ≤ ±5
-5 < X < 5
Entonces, f(x) tiene un valor único ∀ x ∈(-5. 5), entonces la f(x) dada es continua en [-3, 4].
Ahora, derivar f(x) = (25 – x 2 ) 1/2 con respecto a x, obtenemos
f'(x) = 1/2(25 – x 2 ) 1/2-1 d(25 – x 2 )/dx
Entonces, f'(x) existe∀ x ∈ (-3, 4), por lo tanto, f(x) es diferencial en (-3, 4).
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (-3, 4) tal que,
Al elevar al cuadrado ambos lados, obtenemos
49c 2 = 25 – c 2
c2 = 1/2
c = ±1/√2
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (x). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = tan -1 x en [0, 1].
Solución:
Dado que,
f(x) = bronceado -1 x
Aquí, la f(x) dada es continua en [0, 1] y derivable en (0, 1)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 1) tal que,
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xi). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x + 1/x en [1, 3].
Solución:
Dado que,
f(x) = x + 1/x ⇒ (x 2 + 1)/x
Aquí, la f(x) dada es continua en [1, 3] y derivable en (1, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 3) tal que,
c 2 = 3
c = √3 ∈ (1, 3)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xii). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x (x + 4) 2 en [1, 3].
Solución:
Dado que,
f(x) = x (x + 4) 2
Dado que la f(x) = x (x + 4) 2 dada es una función polinomial.
Entonces, la f(x) dada es continua en [1, 3] y derivable en (1, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 3) tal que,
3c 2 + 16c + 16 = 64
3c 2 + 16c – 48 = 0
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xiii) Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 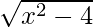 en [2, 4].
en [2, 4].
Solución:
Dado que,
f(x) = x
La f(x) dada existe, si
x2 – 4≥ 0
x2 ≤ 4
x ≤ ±2
-2 < x < 2
Entonces, f(x) tiene un valor único ∀ x ∈(-2. 2), entonces la f(x) dada es continua en [2, 4].
Ahora, derivar f(x) = (x 2 – 4) 1/2 con respecto a x, obtenemos
f'(x) = 1/2(x 2 – 4) 1/2-1 d(x 2 – 4)/dx
Entonces, f'(x) existe∀ x ∈ (2, 4), por lo tanto, f(x) es diferencial en (2, 4).
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (2, 4) tal que,
Al elevar al cuadrado ambos lados, obtenemos
⇒
⇒4c 2 = 12c 2 – 48
⇒8c 2 = 48
⇒c 2 = 6
⇒c = √6 ∈ (2, 4)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xiv). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = x 2 + x – 1 en [0, 4].
Solución:
Dado que,
f(x) = x2 + x – 1
Dado que la f(x) = x 2 + x – 1 dada es una función polinomial.
Entonces, la f(x) dada es continua en [0, 4] y diferenciable en (0, 4)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 4) tal que,
2c + 1 = 20/4
2c + 1 = 5
c = 2 ∈ (0, 4)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xv) Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como establece el teorema del valor medio de Lagrange f(x) = sen x – sen2x – x en [0, π].
Solución:
Dado que,
f(x) = sen x – sen2x – x
Dado que f(x) = sen x – sen2x – x es una función polinomial.
Entonces, la f(x) dada es continua en [0, π] y diferenciable en (0, π)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, π) tal que,
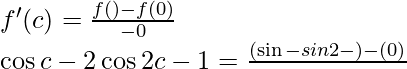
⇒cos c – 2cos2c = -1 + 1
⇒cos – 2(2cos 2 c – 1) = 0
⇒4cos2c – cosc – 2 = 0
⇒
⇒
⇒
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 1 (xvi). Verifique el teorema del valor medio de Lagrange para la siguiente función en el intervalo indicado. En cada uno, encuentre un punto ‘c’ en el intervalo indicado como lo establece el teorema del valor medio de Lagrange f(x) = x 3 – 5x 2 – 3x en [1, 3]
Solución:
Dado que,
f(x) = x 3 – 5x 2 – 3x
Dado que la f(x) = x 3 – 5x 2 – 3x dada es una función polinomial.
Entonces, la f(x) dada es continua en [1, 3] y derivable en (1, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 3) tal que,
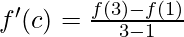
Ahora, f'(c) = 3c 2 – 10c– 3, f(1) = -7, f(3) = -27
3c 2 – 10c – 3 =
3c 2 – 10c – 3 = -10
3c 2 – 10c + 7 = 0
3c 2 – 3c – 7c + 7 = 0
c = 7/3, donde c = 7/3 ∈ (1, 3)
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 2. Discuta la aplicabilidad del teorema del valor medio de Lagrange para la función f(x) = |x| en [-1, 1].
Solución:
Dado que,
f(x) = |x|
Ahora comprobamos la diferenciabilidad en x = 0
volante a la izquierda =
RHD =
LHD ≠ RHD
Aquí, f(x) no es diferenciable en x = 0 ∈ (-1, 1)
Por lo tanto, el teorema del valor medio de Lagrange no es aplicable para el f(x) = \x\ dado.
Pregunta 3. Muestre que el teorema del valor medio de Lagrange no es aplicable a la función f(x) = 1/x en [-1, 1].
Solución:
Dado que,
f(x) = 1/x
Al derivar con respecto a x, obtenemos
Entonces, concluimos que f'(x) no existe en x = 0 ∈ (-1, 1)
Entonces, f(x) tampoco es derivable en (-1, 1)
Por lo tanto, el teorema del valor medio de Lagrange no es aplicable para el f(x) = 1/x dado.
Pregunta 4. Verifique la hipótesis y la conclusión del teorema del valor medio de Lagrange para la función f(x) 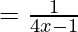 , 1 ≤ x ≤ 4.
, 1 ≤ x ≤ 4.
Solución:
Dado que,
f(x)
Aquí, la f(x) dada tiene un valor único para cada x ∈ [1, 4], por lo que f(x) es continua en [1, 4].
Ahora diferenciamos f(x) con respecto a x, obtenemos

Entonces, aquí f'(x) existe para todo x ∈ (1, 4), por lo tanto, f(x) es diferenciable en (1, 4)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 4) tal que,
(4c – 1) 2 = 45
4c – 1 = ±3√5
Por lo tanto, se verifica el teorema del valor medio de Lagrange.
Pregunta 5. Encuentra un punto en la parábola y = (x – 4) 2 , donde la tangente es paralela a la cuerda que une (4, 0) y (5, 1).
Solución:
Dado que,
f(x) = y = (x – 4) 2 ⇒ x 2 – 8x + 16
También se da que la tangente es paralela a la cuerda que une (4, 0) y (5, 1)
Entonces, consideremos que la cuerda que une los puntos es (4, 5)
Dado que la f(x) = x 2 – 8x + 16 dada es una función polinomial.
Entonces, la f(x) dada es continua en [4, 5] y derivable en (4, 5)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (4, 5) tal que,
2c – 8 = 1
2c = 9
c = 9/2
Asi que,
f(c) = (c – 4) 2
f(c) = (9/2 – 4) 2
f(c) = 1/4
Por lo tanto, (c, f(c)) = (9/2, 1/4) es el punto dado.
Pregunta 6. Encuentra un punto en la curva y = x 2 + x, donde la tangente es paralela a la cuerda que une (0, 0) y (1, 2).
Solución:
Dado que,
f(x) = y = x2 + x
También se da que la tangente es paralela a la cuerda que une (0, 0) y (1, 2)
Entonces, consideremos que la cuerda que une los puntos es (0, 1)
Dado que la f(x) = x 2 + x dada es una función polinomial.
Entonces, la f(x) dada es continua en [0, 1] y diferenciable en (0, 1)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (0, 1) tal que,
2c + 1 = 2
c = 1/2
Asi que,
f(c) = c 2 + c
f(c) = (1/2) 2 + 1/2
f(c) = 3/4
Por lo tanto, (c, f(c)) = (1/2, 3/4) es el punto dado.
Pregunta 7. Encuentra un punto en la probable y = (x – 3) 2 , donde la tangente es paralela a la cuerda que une (3, 0) y (4, 1).
Solución:
Dado que,
f(x) = y = (x – 3) 2 = x 2 – 6x + 9
También se da que la tangente es paralela a la cuerda que une (3, 0) y (4, 1)
Entonces, consideremos que la cuerda que une los puntos es (3, 4)
Dado que la f(x) = x 2 – 6x + 9 dada es una función polinomial.
Entonces, la f(x) dada es continua en [3, 4] y diferenciable en (3, 4)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (3, 4) tal que,
2c = 7
c = 7/2
Asi que,
f(c) = (c – 3) 2
f(c) = (7/2 – 3) 2
f(c) = 1/4
Por lo tanto, (c, f(c)) = (7/2, 1/4) es el punto dado.
Pregunta 8. Encuentra los puntos en la curva y = x 3 – 3x, cuya tangente a la curva es paralela a la cuerda que une (1, -2) y (2, 2).
Solución:
Dado que,
f(x) = y = x 3 – 3x
También se da que la tangente es paralela a la cuerda que une (1, -2) y (2, 2)
Entonces, consideremos que la cuerda que une los puntos es (1, 2)
Dado que la f(x) = x 3 – 3x dada es una función polinomial.
Entonces, la f(x) dada es continua en [1, 2] y derivable en (1, 2)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 2) tal que,
Asi que,
f(c) = (
)3 – 3
f(c) =
Por lo tanto, (c, f(c)) = (
) es el punto dado.
Pregunta 9. Encuentra un punto en la curva y = x 3 + 1 donde la tangente es paralela a la cuerda que une (1, 2) y (3, 28).
Solución:
Dado que,
f(x) = y = x 3 + 1
También se da que la tangente es paralela a la cuerda que une (1, 2) y (3, 28)
Entonces, consideremos que la cuerda que une los puntos es (1, 3)
Dado que la f(x) = x 3 + 1 dada es una función polinomial.
Entonces, la f(x) dada es continua en [1, 3] y derivable en (1, 3)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (1, 3) tal que,
Asi que,
f(c) = c 3 + 1
f(c) = (
) 3 + 1
Por lo tanto, (c, f(c)) = (
, (
) 3 + 1) es el punto dado.
Pregunta 10. Sea c una curva definida paramétricamente como x = a cos 3 , y = a sen 3 , 0 ≤ ≤ π/2. Determine un punto P en C, donde la tangente a C sea paralela a la cuerda que une los puntos (a, 0) y (0, a).
Solución:
Consideremos que el punto P sea (x, y)
Entonces, dado que,
x = a cos 3
y = un pecado 3
Ahora encontramos la pendiente de la tangente
….(3)
Entonces, derivar eq(1), wrt θ, obtenemos,
porque 2
Ahora, derivar eq(2), wrt θ, obtenemos,
un pecado 2
Ahora ponga todos estos valores en la ecuación (3), obtenemos
dy/dx = cos 2 a sen 2
Ahora los dos puntos dados son (a, 0) y (0, a).
Entonces, la pendiente de la cuerda dada, m = a – 0/0 – a = -1
Según la pregunta se da que el punto C es paralelo a la cuerda
Entonces, pendiente de la tangente = pendiente de la cuerda
-tanθ = -1
θ = π/4
Ahora pon el valor de θ en la ecuación (1) y (2), obtenemos los valores del punto P
x = a cos 3 π/4) = a/2√2
y = a sen 3 π/4= a/2√2
Entonces, el punto P(a/2√2, a/2√2)
Pregunta 11. Utilizando el teorema del valor medio de Lagrange, demuestre que (b – a)sec 2 a < tanb – tana < (b – a)sec 2 b donde 0 < a < b < π/2.
Solución:
Dado que,
f(x) = tan x, x ∈ [a, b] tal que 0 < a < b < π/2}
Entonces, la f(x) dada es continua en [a, b] y derivable en (a, b)
Por lo tanto, se cumplen ambas condiciones del teorema del valor medio de Lagrange.
Entonces, existe un punto c ∈ (a, b) tal que,
….(i)
Entonces, c ∈ (a, b)
segundo 2 a <
Ahora, usando la ecuación (i), obtenemos
(b – a) seg 2 a < (tan b – tan a) < (b – a) seg 2 b
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
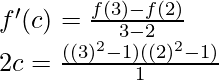
![Procesado por QuickLaTeX.com f'(c)=\frac{f(1)-f(0)}{1-0}\\ 3c^2-4c-1=\frac{[(1)^2-2(1)^2 -(1)+3]-3}{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f77aac287d21e590bbae00e61046a3a8_l3.png)