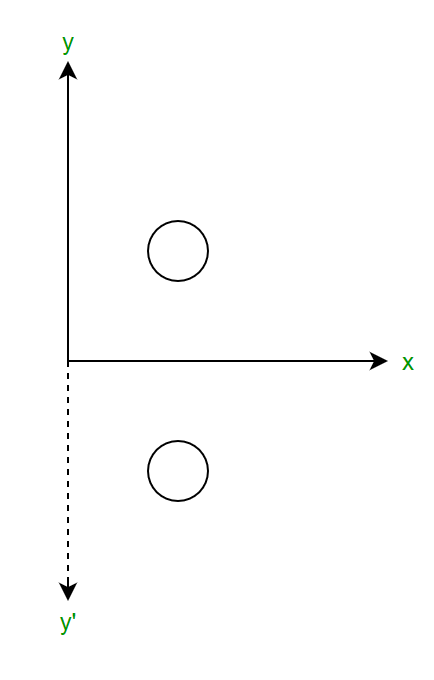
La reflexión se ocupa de obtener una imagen especular del objeto 2D.
Sobre el eje x:
Si P(x, y) es el punto en el plano xy, entonces P'(x’, y’) es la reflexión sobre el eje x dada como x’=x ; y’=-y
Forma de array:
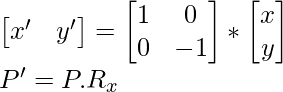
Sobre el eje y:
Si P(x, y) es el punto en el plano xy, entonces P'(x’, y’) es la reflexión sobre el eje y dada como x’=-x ; y’=y

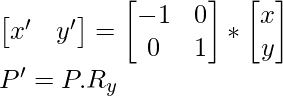
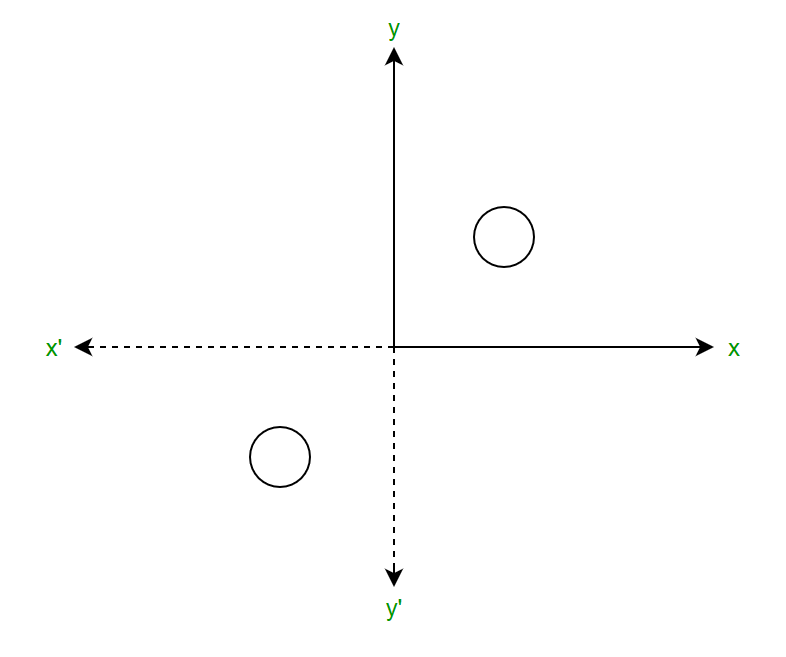
A lo largo del origen:
Si P(x, y) es el punto en el plano xy, entonces P'(x’, y’) es la reflexión sobre el origen dada como x’=-x ; y’=-y
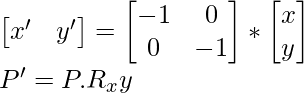
Acerca de la línea x=y: para hacer esto, mueva la línea x=y a cualquiera de los ejes. En el diagrama dado, el ángulo de rotación es de 45 ° ya que los puntos se trazan como (0, 0), (1, 1), (2, 2), etc.

Imponiendo la recta en el sentido de las agujas del reloj (-45 o ) imponiéndola en el eje x tenemos,
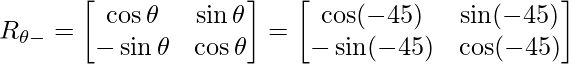
Sabemos,
![]()
y
![]()
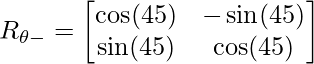
Ahora realice la reflexión a lo largo del eje x,
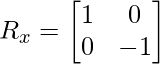
Ahora gire la línea hacia atrás 45 o en sentido contrario a las agujas del reloj,
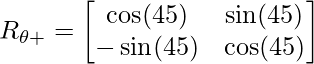
Ahora bien, si P(x, y) es el punto en el plano xy, entonces P'(x’, y’) es la reflexión sobre la línea x=y dada como x’=y ; y’=x
Forma matricial:
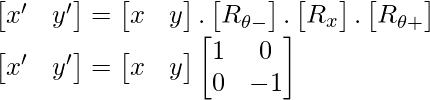
Problema : Se da un triángulo con las coordenadas p (5 4), q (2 2), r (5 6) necesitamos reflejarlo a lo largo del eje Y.
Respuesta : Nos dan las coordenadas p, q, r como se muestra en la figura-

Reflexión triangular en gráficos 2D
Ahora, aplicamos la condición de reflejar un objeto bidimensional a lo largo del eje Y:
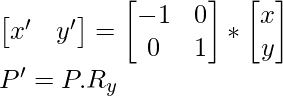
La primera coordenada p, se convierte en p’ después de la reflexión:
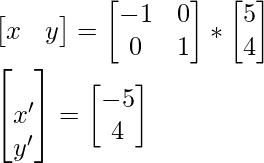
Segunda coordenada q, se convierte en q’ después de la reflexión:
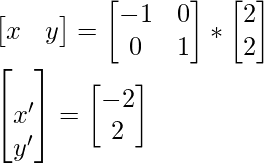
La tercera coordenada r del triángulo se convierte en r’ después de la reflexión:
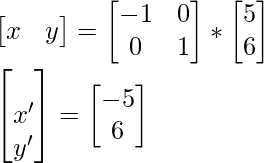
Después de reflejar el triángulo sobre el punto del eje Y p, q, r se convierte en p’, q’, r’:
p(5, 4) = p'(-5, 4) , q(2, 2) = q'(-2, 2) , r(5, 6) = r'(-5, 6)
El objeto reflectante aparecería como:
