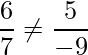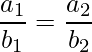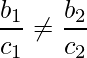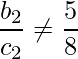Número de soluciones de un sistema de ecuaciones algebraicamente

Una declaración de que dos expresiones matemáticas de una o más variables son idénticas se llama ecuación . Las ecuaciones lineales son aquellas en las que las potencias de todas las variables involucradas son iguales. El grado de una ecuación lineal es siempre uno. Una solución del par simultáneo de ecuaciones lineales es un par de valores de las variables «x» e «y» que satisfacen todas las ecuaciones en el conjunto de ecuaciones especificado.

Par de ecuaciones lineales en dos variables

Una ecuación que se puede poner en la forma ax + by + c = 0 , donde a, b y c son números reales, y a y b no son cero, se llama ecuación lineal en dos variables x e y. (o esta condición debe cumplirse cuando a y b no son ambos cero por a ² + b ² ≠ 0).

ej.: Considere un par de ecuaciones lineales en dos variables sea 3x + 2y = 6,

Sustituye x = 2 e y = 0 en el lado izquierdo (LHS) como:

⇒ IZQ = 3(2) + 2(0)

= 6 + 0

= 6 = lado derecho

Por lo tanto, x = 2 y y = 0 es una solución de la ecuación 2x + 3y = 6.

Ahora, si se sustituye x = 1 y y = 1 en la ecuación 2x + 3y = 6, entonces:

IZQ = 3(1) + 2(1)

= 3 + 2

= 5 ≠ lado derecho

Por lo tanto, x = 1 e y = 1 no es una solución de la ecuación.

Algebraicamente, esto indica que el punto (2, 0) se encuentra en la línea que representa la ecuación 3x + 2y = 6, y el punto (1, 1) no se encuentra en ella.

Así, toda solución que satisfaga la ecuación es un punto en la recta que la representa.

Dos ecuaciones lineales como esta, que tienen dos variables x e y. Ecuaciones como estas se llaman un par de ecuaciones lineales en dos variables .

Algebraicamente, la forma general para un par de ecuaciones lineales en dos variables x e y es:

a ₁ x + b ₁ y + c ₁ = 0 y

un ₂ x + _{segundo 2} y + c ₂ = 0

donde a ₁ , b ₁ , c ₁ , a ₂ , b ₂ , c ₂ son todos números reales ( ∈ R ) y a ₁² + b ₁² ≠ 0, a ₂² + b ₂ ² ≠ 0.

Diferentes casos posibles para el par de ecuaciones lineales en dos variables

Hay tres casos diferentes para tres tipos diferentes de rectas: rectas secantes, paralelas y coincidentes para determinar el par de ecuaciones lineales en dos variables.

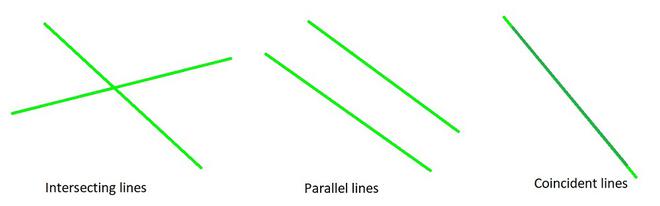
Las líneas pueden intersecarse en un solo punto.

Como resultado, el par de ecuaciones tiene una solución única (par de ecuaciones consistente).

por ejemplo: 2x – 4y = 0 y 6x + 8y – 40 = 0

Líneas que se cruzan: 2x – 4y = 0 y 6x + 8y – 40 = 0

Las líneas pueden ser paralelas entre sí.

Como resultado, las ecuaciones no tienen solución (par de ecuaciones inconsistentes).

por ejemplo: 2x + 4y – 8 = 0 y 4x + 8y – 24 = 0

Líneas paralelas: 2x + 4y – 8 = 0 y 4x + 8y – 24 = 0

Las líneas pueden ser coincidentes .

Como resultado, las ecuaciones tienen infinitas soluciones (par de ecuaciones dependientes o consistentes)

por ejemplo: 4x + 6y – 18 = 0 y 8x + 12y – 36 = 0

Líneas que se cruzan: 4x + 6y – 18 = 0 y 8x + 12y – 36 = 0

Ahora, supongamos el par de ecuaciones: a ₁ x + b ₁ y + c ₁ = 0 y a ₂ x + b ₂ y + c ₂ = 0 ahora su interpretación gráfica y algebraica correspondiente a las relaciones de comparación se da como:

\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2}

Comparación de proporciones	Gráfico Representación	Algebraico Interpretación
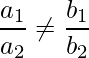$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$	Intersección Líneas	exactamente uno Solución (única)
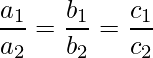$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2}$	Coincidente Líneas	infinitamente muchos soluciones
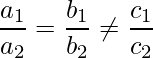$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$	Paralela Líneas	Sin solución

Problemas de muestra

Problema 1: Encuentra la representación gráfica y especifica el número de soluciones de los siguientes pares de ecuaciones lineales: 8x – 4y + 10 = 0 y 4x – 2y + 9 = 0.

Solución:

Para el par dado de ecuaciones lineales:

a ₁ = 8, b ₁ = -4, c ₁ = 10 y

un ₂ = 4, _{segundo 2} = -2, c ₂ = 9

Por lo tanto,

un ₁ / un ₂ = 8 / 4 = 2

b ₁ / b ₂ = -4 / -2 = 2 y

do ₁ / do ₂ = 10 / 9

Esto implica que:

$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$

Por lo tanto, los pares de ecuaciones lineales dados no tienen solución y las líneas son paralelas y nunca se intersecan entre sí.

Problema 2: Determinar el número de soluciones de los siguientes pares de ecuaciones lineales: 6x + 2y = 4 y 7x – 3y = 13.

Para el par dado de ecuaciones lineales:

a ₁ = 6, b ₁ = 2, c ₁ = -4 y

a ₂ = 7, b ₂ = -3, c ₂ = -13

Por lo tanto,

un ₁ / un ₂ = 6 / 7

b ₁ / b ₂ = 2 / -3 y

do ₁ / do ₂ = -4 / -13

Esto implica que:

$\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$

Por lo tanto, los pares de ecuaciones lineales dados tienen una solución única y las líneas se intersecan exactamente en un punto.

Problema 3: Determinar la representación gráfica y el número de soluciones de los siguientes pares de ecuaciones lineales: 6x – 5y = 11; – 12x +10y = –22.

Para el par dado de ecuaciones lineales:

a ₁ = 6, b ₁ = -5, c ₁ = -11 y

a ₂ = -12, b ₂ = 10, c ₂ = 22

Por lo tanto,

un ₁ / un ₂ = 6 / -12 = -1 / 2

b ₁ / b ₂ = -5 / 10 = -1 / 2 y

do ₁ / do ₂ = -11 / 22

Esto implica que:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$

Por lo tanto, los pares de ecuaciones lineales dados tienen infinitas soluciones y las líneas son coincidentes.

Problema 4: Forme el par de ecuaciones lineales en los siguientes problemas verbales y encuentre sus soluciones gráficamente.

Hay 20 estudiantes en una clase. Si el número de niños es 6 más que el número de niñas, encuentre el número de niños y niñas en la clase.

Solución:

Considere, el número de niñas sea x y el número de niños sea y.

Por lo tanto, de acuerdo con las condiciones dadas:

x + y = 20 ……(1)

x – y = 6 ……(2)

Para construir el gráfico se necesita determinar las soluciones de la ecuación dada.

Para la ecuación (1): x + y = 20, las soluciones son:

X y

0 20

20 0

Para la ecuación (2): x – y = 6, Entonces, las soluciones son:

X y

0 -6

6 0

Por lo tanto, trazando los puntos anteriores para la ecuación (1) y (2) como:

Ahora, del gráfico se puede concluir que las líneas dadas se cortan entre sí en el punto (13, 7).

Por lo tanto, el número de niñas es 7 y el número de niños es 13 en una clase.

X	y
0	20
20	0

X	y
0	-6
6	0

Problema 5: Determinar otra ecuación lineal en dos variables tal que se forme:

(i) líneas de intersección con la línea 6x + 7y – 8 = 0.

(ii) líneas paralelas con la línea 4x-5y-8=0.

Solución:

(i)

Para que un par de rectas se corten, deben cumplir las condiciones dadas:

$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$

Al reordenar la expresión anterior como:

$\frac{a_1}{b_1} \neq \frac{a_2}{b_2}$

Por lo tanto, en la ecuación la relación no debe ser 6/7.

Entonces, otra ecuación puede ser 5x – 9y + 9 = 0

donde la relación es 5/-9 y

$\dfrac{6}{7} \neq \dfrac{5}{-9}$

(ii)

Para que un par de rectas sean paralelas, deben cumplir las condiciones dadas:

$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$

Al reordenar la expresión anterior como:

$\dfrac{a_1}{b_1} = \dfrac{a_2}{b_2}$

$\dfrac{b_1}{c_1} \neq \dfrac{b_2}{c_2}$

Por lo tanto, la ecuación requerida a ₂ / b ₂ debe estar en una proporción de 4 / -5 y b ₂ / c ₂ no debe ser igual a -5 / -8.

Entonces, otra ecuación puede ser 8x – 10y + 9 = 0

donde la relación a ₂ / b ₂ es 8/-10 = -8/10 y

$\dfrac{b_2}{c_2} \neq \dfrac{5}{8}$