Dado un número N , la tarea es encontrar la suma de la diferencia de Hamming de números consecutivos de 0 a N.
La distancia de Hamming entre dos enteros es el número de bits que son diferentes en la misma posición en ambos números.
Ejemplos:
Entrada: 5
Salida: 8
Explicación:
Diferencia entre (0, 1) = 1, (1, 2) = 2,
(2, 3) = 1, (3, 4) = 3, (4, 5) = 1.
Entonces la suma total es 1 + 2 + 1 + 3 + 1 = 8
Entrada: 9
Salida: 16
Enfoque ingenuo y logarítmico: consulte Suma de diferencias de bits para números de 0 a N para el enfoque ingenuo y un enfoque logarítmico para calcular la suma en función de verificar si N es potencia de 2 o no.
Enfoque: En este artículo, se analiza un enfoque basado en la observación del número de cambios que se producen en todos los bits, desde el LSB hasta el MSB.
Siga los pasos a continuación para resolver el problema:
- Se puede observar que el bit menos significativo cambiará N veces. El segundo bit menos significativo cambiará de piso (N/2) veces (es decir , (N – 1)/2 si N es impar y N/2 si N es par). Por lo tanto, el i -ésimo bit cambiará de piso (N/2 i ) veces.
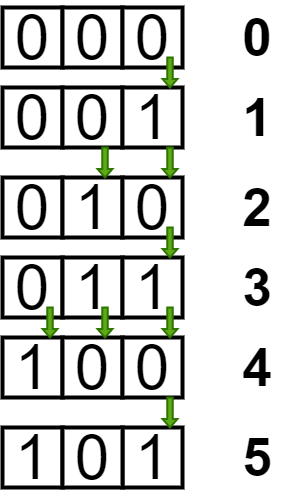
- Por lo tanto, para resolver este problema podemos simplemente almacenar la suma
N + piso(N/2) + … piso(N/2 i )
- hasta que el término no se haga cero.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ Program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to calculate and
// return the hamming distance
// between all consecutive
// numbers from 0 to N
int TotalHammingDistance(int n)
{
int i = 1, sum = 0;
while (n / i > 0) {
sum = sum + n / i;
i = i * 2;
}
return sum;
}
// Driver Code
int main()
{
int N = 9;
cout << TotalHammingDistance(N);
return 0;
}
Java
// Java program to implement the
// above approach
import java.util.*;
class GFG{
// Function to calculate and
// return the hamming distance
// between all consecutive
// numbers from 0 to N
static int TotalHammingDistance(int n)
{
int i = 1, sum = 0;
while (n / i > 0)
{
sum = sum + n / i;
i = i * 2;
}
return sum;
}
// Driver code
public static void main(String[] args)
{
int N = 9;
System.out.println(TotalHammingDistance(N));
}
}
// This code is contributed by offbeat
Python3
# Python3 program to implement # the above approach # Function to calculate and # return the hamming distance # between all consecutive # numbers from 0 to N def TotalHammingDistance(n): i = 1 sum = 0 while (n // i > 0): sum = sum + n // i i = i * 2 return sum # Driver Code if __name__ == '__main__': N = 9 print(TotalHammingDistance(N)) # This code is contributed by mohit kumar 29
C#
// C# Program to implement
// the above approach
using System;
class GFG{
// Function to calculate and
// return the hamming distance
// between all consecutive
// numbers from 0 to N
static int TotalHammingDistance(int n)
{
int i = 1, sum = 0;
while (n / i > 0)
{
sum = sum + n / i;
i = i * 2;
}
return sum;
}
// Driver Code
public static void Main()
{
int N = 9;
Console.Write(TotalHammingDistance(N));
}
}
// This code is contributed by Code_Mech
Javascript
<script>
// Javascript program for the above approach
// Function to calculate and
// return the hamming distance
// between all consecutive
// numbers from 0 to N
function TotalHammingDistance(n)
{
let i = 1, sum = 0;
while (Math.floor(n / i) > 0)
{
sum = sum + Math.floor(n / i);
i = i * 2;
}
return sum;
}
// Driver Code
let N = 9;
document.write(TotalHammingDistance(N));
// This code is contributed by code_hunt.
</script>
16
Complejidad temporal: O(logN)
Espacio auxiliar: O(1)