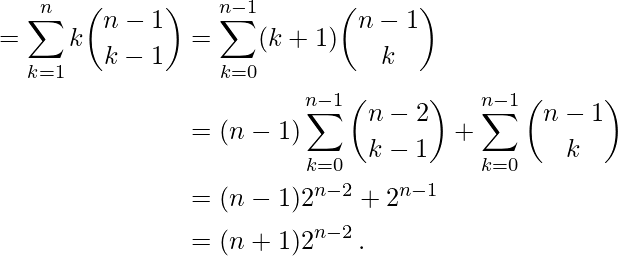Cuente los números presentes en las particiones de N

Dado un número entero N , la tarea es contar los números en particiones enteras ordenadas de N .
Ejemplos:

Entrada: N = 3
Salida: 8 Las
particiones enteras de N(=3) son {{1 + 1 + 1}, {1 + 2}, {2 + 1}, {3}}.
Los números en la partición de enteros de N son: {1, 1, 1, 1, 2, 2, 1, 3}
Por lo tanto, la cuenta de números en las particiones de enteros de N(=3) es 8.

Entrada: N = 4
Salida: 20

Enfoque: El problema se puede resolver con base en las siguientes observaciones:

Recuento de formas de dividir N en exactamente k particiones =

$\binom{n-1}{k-1}$

Por lo tanto, el conteo de números en particiones enteras ordenadas de N es

$\begin{align*} = \sum_{k=1}^nk\binom{n-1}{k-1}&=\sum_{k=0}^{n-1}(k+1)\binom{n-1}k\\ &=(n-1)\sum_{k=0}^{n-1}\binom{n-2}{k-1}+\sum_{k=0}^{n-1}\binom{n-1}k\\ &=(n-1)2^{n-2}+2^{n-1}\\ &=(n+1)2^{n-2}\, . \end{align*}$

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program to implement
// the above approach 
#include <bits/stdc++.h>
using namespace std;
 
// Function to count of numbers in
// ordered partitions of N
int CtOfNums(int N)
{
  
    // Stores count the numbers in
    // ordered integer partitions
    int res = (N + 1) * (1 << (N - 2));
  
    return round(res);
}
  
// Driver Code
int main()
{
    int N = 3;
     
    cout << CtOfNums(N);
}
 
// This code is contributed by code_hunt

Java

// Java program to implement
// the above approach 
import java.io.*;
 
class GFG{
  
// Function to count of numbers in
// ordered partitions of N
static int CtOfNums(int N)
{
  
    // Stores count the numbers in
    // ordered integer partitions
    int res = (N + 1) * (1 << (N - 2));
  
    return Math.round(res);
}
  
// Driver Code
public static void main (String[] args)
{
    int N = 3;
  
    System.out.print(CtOfNums(N));
}
}
 
// This code is contributed by code_hunt

Python3

# Python3 program to implement
# the above approach
 
# Function to count of numbers in
# ordered partitions of N
def CtOfNums(N):
 
    # Stores count the numbers in
    # ordered integer partitions
    res = (N + 1) * (1<<(N - 2))
 
    return round(res)
 
# Driver code
if __name__ == '__main__':
    N = 3
    print(CtOfNums(N))

C#

// C# program to implement
// the above approach 
using System;
 
class GFG{
  
// Function to count of numbers in
// ordered partitions of N
static int CtOfNums(int N)
{
  
    // Stores count the numbers in
    // ordered integer partitions
    double res = (N + 1) * (1 << (N - 2));
  
    return (int)Math.Round(res);
}
  
// Driver Code
public static void Main ()
{
    int N = 3;
  
    Console.Write(CtOfNums(N));
}
}
 
// This code is contributed by code_hunt

Javascript

<script>
 
// Javascript program to implement
// the above approach 
 
// Function to count of numbers in
// ordered partitions of N
function CtOfNums(N)
{
  
    // Stores count the numbers in
    // ordered integer partitions
    var res = (N + 1) * (1 << (N - 2));
  
    return Math.round(res);
}
  
// Driver Code
var N = 3;
document.write(CtOfNums(N));
 
</script>

Producción:

Complejidad de tiempo: O(log ₂ N)
Espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por spp____ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta