Pregunta 1. Usando la integración, encuentre el área de la región acotada entre la línea x = 2 y la parábola y 2 = 8x
Solución:
Aquí,
Las ecuaciones dadas son:
x = 2 ……..(1)
y 2 = 8x ……..(2)
Aquí,
La ecuación (1) representa una línea paralela al eje y y la ecuación (2) representa una parábola con vértice en el origen y eje x,
Aquí está el boceto aproximado
Tenemos que encontrar el área de la región sombreada. Lo cortamos en rectángulo vertical ancho de rectángulo = △x,
Longitud = (y – 0) = y
Área del rectángulo = y△x
Este rectángulo puede moverse horizontalmente de x = 0 a x = 2
Área requerida = región sombreada OCBO
= 2 (Región sombreada OABO)
=
Área requerida =
unidades cuadradas.
Pregunta 2. Usando la integración, encuentre el área de la región delimitada por la línea y – 1 = x, el eje x y las ordenadas x = -2 y x = 3.
Solución:
El área de búsqueda de la región delimitada por el eje x las ordenadas x = -2 y x = 3
y – 1 = x ………….(1)
La ecuación (1) es una línea que se encuentra en los ejes en (0, 1) y (-1, 0)
Aquí, está el boceto aproximado.
El área requerida está encerrada entre las líneas.
Área requerida = Región ABCA + Región ADEA
Pregunta 3. Halla el área de la región delimitada por la parábola y 2 = 4ax y la recta x = a
Solución:
Aquí tenemos que encontrar el área de la región que está delimitada por
x = un ………(1)
y
y2 = 4a ………(2)
La ecuación (1) representa una línea paralela al eje y y la ecuación (2) representa una parábola con vértice en el origen y eje como eje x.
Aquí, está el boceto aproximado.
Aquí tenemos que encontrar el área entre la región,
Por lo tanto, córtela en rectángulos de
Ancho = △x
Longitud = y – 0 = y
Área del rectángulo = y△x
Este supuesto triángulo puede ir de x = 0 a x = a.
Área requerida = Región OCBO
= 2 (Región OABO)
área requerida =
unidades cuadradas
Pregunta 4. Encuentra el área que se encuentra sobre el eje x y debajo de la parábola y = 4x – x 2 .
Solución:
Tenemos que encontrar aquí el área delimitada por el eje x y la parábola.
y = 4x – x2
x2 – 4x +4 = -y + 4
(x – 2)2 = -(y – 4) ……….(1)
La ecuación (1) representa una parábola hacia abajo con vértice (2, 4) y que pasa por (0, 0) y (0, 4).
Aquí está el boceto aproximado
Aquí la región sombreada representa el área requerida.
Cortamos la región en rectángulos de aproximación
Ancho = △x
Longitud = y – 0 = y
Área del rectángulo = y△x
Este rectángulo de aproximación se desliza de x = 0 a x = a
De este modo,
Área requerida = Región OABO
área requerida =
unidades cuadradas
Pregunta 5. Dibuja un bosquejo aproximado para indicar la región delimitada entre la curva y 2 = 4x y la línea x = 3. Además, encuentra el área de esta región.
Solución:
Tenemos que encontrar el área delimitada por
y2 = 4x ……..(1)
y
x = 3 ………..(2)
La ecuación (1) representa una parábola con vértice en el origen y eje como eje x y la ecuación (2) representa una línea paralela al eje y
Aquí está el boceto aproximado
La región sombreada representa el área requerida que hemos cortado en forma de rectángulo de
Ancho = △x
Longitud = y – 0 = y
Este rectángulo de aproximación se desliza de x = 0 a x = 3
Área requerida = Región OCBO
= 2(Región OABO)
área requerida =
unidades cuadradas
Pregunta 6. Haz un bosquejo aproximado de la gráfica de la función y = 4 – x 2 , 0 ≤ x ≤ 2 y determina el área encerrada por la curva , el eje x y la recta x = 0 y x = 2.
Solución:
Aquí encontraremos el área delimitada por
y = 4 – x2
x2 = -(y – 4) ……….(1)
x = 0 ………(2)
x = 2 ……….(3)
La ecuación (1) representa una parábola hacia abajo con vértice en (0, 4) y que pasa por (2, 0), (-2, 0). La ecuación (2) representa el eje y y la ecuación (3) representa una línea paralela al eje y.
Aquí hay un boceto aproximado
La región sombreada representa el área requerida que hemos cortado en forma de rectángulo de
Ancho = △x
longitud = y – 0 = y
Este rectángulo de aproximación se desliza de x = 0 a x = 2
Área requerida = Región OABO
Área requerida =
unidades cuadradas.
Pregunta 7. Dibuja la gráfica de 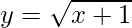 en [0, 4] y determina el área de la región encerrada por la curva, el eje x y la línea x = 0 y x = 4.
en [0, 4] y determina el área de la región encerrada por la curva, el eje x y la línea x = 0 y x = 4.
Solución:
Aquí, encontraremos el área encerrada por el eje x y
y2 = x + 1 …….(1)
x = 0 ………(2)
x = 4 ………(3)
La ecuación (1) representa una parábola con vértice en (-1, 0) y que pasa por (0, 1) y (0, -1). La ecuación (2) representa el eje y y la ecuación (3) representa una línea paralela al eje y que pasa por (4, 0).
Por lo tanto, aquí está el boceto aproximado;
La región sombreada representa el área requerida que hemos cortado en forma de rectángulo de
Ancho = △x
Longitud = y – 0 = y
Área del rectángulo = y△x
Este rectángulo de aproximación se desliza de x = 0 a x = 4
Área requerida = Región OCDE
Área requerida = unidades cuadradas
o
unidades cuadradas.
Pregunta 8. Encuentre el área bajo la curva 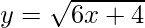 sobre el eje x desde x = 0 hasta x = 2. Dibuje también un bosquejo de la curva.
sobre el eje x desde x = 0 hasta x = 2. Dibuje también un bosquejo de la curva.
Solución:
Aquí, encontraremos el área encerrada por el eje x
x = 0,
x = 2 ………(1)
y2 = 6x + 4 ……….(2)
La ecuación (1) representa el eje y y una línea paralela al eje y que pasa por (2, 0). La ecuación (2) representa una parábola con vértice en
y pasa por los puntos (0, 2), (0, -2).
Por lo tanto, aquí está el boceto aproximado;
La región sombreada representa el área requerida que hemos cortado en forma de rectángulo de
Ancho = △x
Longitud = y – 0 = y
Área del rectángulo = y△x
Este rectángulo de aproximación se desliza de x = 0 a x = 2,
Área requerida = Región OABCO
Área requerida =
unidades cuadradas.
Pregunta 9. Dibuja el bosquejo aproximado de y 2 + 1 = x, x ≤ 2. Encuentra el área encerrada por la curva y la línea x = 2.
Solución:
Aquí, encontraremos el área encerrada por el eje x
y2 = x + 1 ……….(1)
y
x = 2 ……………(2)
La ecuación (1) es una parábola con vértice en (0, 1) y eje como eje x.
La ecuación (2) representa una línea paralela al eje y que pasa por (2, 0)
Por lo tanto, aquí está el boceto aproximado;
La región sombreada representa el área requerida que hemos cortado en forma de rectángulo de
Ancho = △x
Longitud = y – 0 = y
Área del rectángulo = y△x
Este rectángulo de aproximación se desliza de x = 0 a x = 2,
Área requerida = Región ABCA
= 2 (Región AOCA)
Área requerida =
unidades cuadradas.
Pregunta 10. Dibuje un bosquejo aproximado de la gráfica de la curva 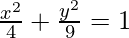 y evalúe el área de la región debajo de la curva y arriba del eje x
y evalúe el área de la región debajo de la curva y arriba del eje x
Solución:
Aquí, podemos observar que la elipse es simétrica con respecto al eje x.
Área delimitada por elipse =
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2y\ dx\\ =2\times2\sqrt2\int_0^2\sqrt{x}\ dx\\ =4\sqrt2\left[\frac{2}{3}\times\sqrt{x}\right]_0^2\\ =4\sqrt2\left[\left(\frac{2}{3}\times2\sqrt2\right)-\left(\frac{2}{3}\right)\times0\sqrt0\right]\\ =4\sqrt2\left(\frac{4\sqrt2}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-821d02ded30051624b641f6583b21f28_l3.png)

![Rendered by QuickLaTeX.com \displaystyle A=\int^3_{-1}y\ dx + \left|\int^{-1}_{-2}y\ dx\right|\\ =\int_{-1}^{3}(x+1)dx+\left|\int_{-2}^{-1}(x+1)dx\right|\\ =\left(\frac{x^2}{2}+x\right)_{-1}^3+\left|\left(\frac{x^2}{2}+x\right)_{-2}^{-1}\right|\\ =\left[\left(\frac{9}{3}+3\right)-\left(\frac{1}{2}-1\right)\right]+\left|\left(\frac{1}{2}-1(2-2)\right)\right|\\ =\left[\frac{15}{2}+\frac{1}{2}\right]+\left|-\frac{1}{2}\right|\\ =8+\frac{1}{2}\\ A=\frac{17}{2}\ square\ units.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a38870871201884a18f5d1bbe42cd5c3_l3.png)

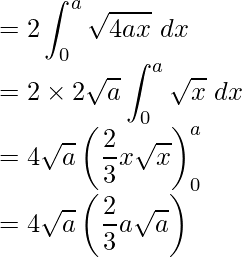

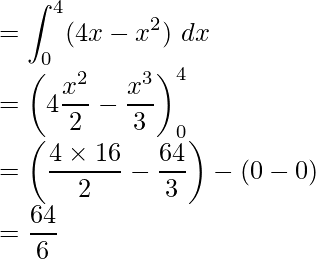

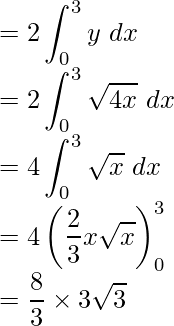

![Rendered by QuickLaTeX.com \displaystyle =\int_0^2(4-x^2)\ dx\\ =\left(4x-\frac{x^3}{3}\right)_0^2\\ =\left[4(2)-\frac{(2)^3}{3}\right]-[0]\\ =\left[\frac{24-8}{3}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c747aff426265e97fcc16117ddb49595_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_0^4y\ dx\\ =\int_0^4\sqrt{x+1}\ dx\\ =\left(\frac{2}{3}(x+1)\sqrt{x+1}\right)_0^4\\ =\frac{2}{3}[((4+1)\sqrt{4+1})-((0+1)\sqrt{0+1})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d40e147ba2e28244aaf174140bf79d14_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_0^2\sqrt{6x+4}\ dx\\ =\left(\frac{2}{3}\frac{(6x+4)\sqrt{6x+4}}{6}\right)_0^2\\ =\frac{1}{9}[((12+4)\sqrt{12+4})-((0+4)\sqrt{0+4})]\\ =\frac{1}{9}[16\sqrt{16}-4\sqrt{4}]\\ =\frac{1}{9}(64-8)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b87798388077b98e3eedf33b24325437_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =2\int_1^2y\ dx\\ =2\int_1^2\sqrt{x-1}\ dx\\ =2\left(\frac{2}{3}(x-1)\times\sqrt{x-1}^2\right)_1^2\\ =\frac{4}{3}[((2-1)\sqrt{2-1})-((1-1)\sqrt{1-1})]\\ =\frac{4}{3}(1-0)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b8caf053c8117eed957b1baa9bb24c0_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2 y\ dx\\ = 2\int_0^23\sqrt{1-\frac{x^2}{4}}\ dx\\ =3\int\sqrt{4-x^2}\ dx\\ =3\left[\frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}sin^{-1}\frac{x}{2}\right]_0^2\\ =3[1(0)+2sin^{-1}-0-2sin^{-1}(0)]\\ =3[\pi]\\ =3\pi\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd10c90185ff60923b7d4931a13db35c_l3.png)