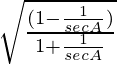Demuestre que √(sec θ – 1)/(sec θ + 1) = cosec θ – cot θ.

El propio nombre de la trigonometría dice que es un tema que trata sobre la geometría de los triángulos y es muy útil para situaciones en las que se necesita saber cuándo hay algunos lados dados y necesitamos las relaciones entre los lados o los ángulos entre los lados. En trigonometría tenemos diferentes razones que son sen A, cos A, tan A, cot A, sec A, cosec A con la ayuda de las cuales se puede obtener la relación entre los lados y el ángulo entre los lados del triángulo.

Funciones trigonométricas

Las funciones trigonométricas definen la relación entre los lados y los ángulos y los ejemplos son sin A, cos A, tan A, cot A, sec A, cosec A. Estas seis funciones muestran la relación entre los lados del triángulo de ángulos rectos, es decir, base, altura e hipotenusa. Los ejemplos son,

sen(A + B) = sen A cos B + cos A sen B
sen(A – B) = sen A cos B – cos A sen B
cos (A + B) = cos A cosB – sen AsinB
cos (A – B) = cos A cos B + sen A sen B
bronceado (A + B) = bronceado A + bronceado B/ 1 – bronceadoA bronceadoB
bronceado (A – B) = bronceado A – bronceado B/ 1+ bronceado Atan B

Identidades trigonométricas

La relación entre diferentes funciones trigonométricas es una identidad trigonométrica. Las identidades son muy útiles para probar la desigualdad en las ecuaciones trigonométricas. Las identidades también se utilizan para simplificar ecuaciones trigonométricas complejas. Las seis razones trigonométricas están relacionadas entre sí de manera que sen es el recíproco de cosec, y así sucesivamente. Echemos un vistazo a algunas identidades trigonométricas básicas,

Tan A = sen A/cos A
sen A = 1/coseg A
cos A = 1/seg A
Tan A = 1/cuna A

Identidades de doble ángulo

sen 2A = 2sen Acos A
cos2A = cos²A – sen²A
bronceado 2A = 2 bronceado A / (1 – bronceado ²A)

Identidades de triple ángulo

sen 3A = 3 sen A – 4 sen³ A
cos3A = 4cos³A – 3 cosA
tan 3A = (3 tan A – tan³A)/(1 – 3 tan² A)

Pruebalo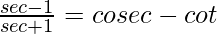 $√\frac{sec θ - 1}{sec θ + 1} = cosec θ - cot θ$

Hay identidades básicas que se requieren para resolver el enunciado del problema anterior, veamos algunas de las identidades básicas de las 6 funciones trigonométricas que se requieren en este caso,

Identidades de requisito previo utilizadas en la prueba

seg ² A – bronceado ² A =1
cosec A = 1/sen A
cos A/sen A = cot A
cuna A/2 = $\sqrt\frac{1+cosA}{1-cosA}$
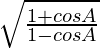
sen ² A = 1 – cos ² A
a ² – b ² = (a + b)(a – b)
(a – b)/c = a/c – b/c
segundo A = 1/cos A

Ecuación trigonométrica dada

$\sqrt\frac{secA -1}{secA+1}$ = cosec A- cot A

IZQ = $\sqrt\frac{secA -1}{secA+1}$

RHS = cosec A – cuna A

Prueba derivada del lado LHS

Dado LHS

$\sqrt\frac{secA -1}{secA+1}$

Paso 1

Multiplicando con (sec A – 1)/(sec A – 1) que es igual a 1 para traer el grado de 1 que está presente en RHS.

= $\sqrt\frac{(secA -1)(secA-1)}{(secA+1)(secA-1)}$

Paso 2

Simplificando la ecuación obtenida en el paso – 2 por más

= $\sqrt\frac{(secA -1)^2}{sec^2A-1}$

= $\sqrt\frac{(secA -1)^2}{tan^2A}$

= (seg A – 1)/tan A

Paso 3

Rompiendo la ecuación en el paso – 2 en forma general

= (seg A/tan A) – (1/tan A)

= ((1/cos A)/(sen A /cos A)) – (1/tan A)

= (1/sen A) – (1/tan A)

Paso 4

Sustituyendo con fórmulas estándar en la ecuación obtenida en el paso – 3

= cosec A – cuna A

Del paso – 4 se puede concluir que LHS = cosec A – cot A que es igual a RHS y, por lo tanto,

cosec A – cuna A = cosec A – cuna A

LHS = RHS

Por lo tanto Probado.

Derivación de la prueba del lado derecho

Dado RHS: cosec θ – cot θ

Paso 1

Simplificar la ecuación sustituyendo fórmulas estándar

(1/sen A) – (cos A/sen A)

= (1 – cos A)/(sen A)

Paso 2

Simplificando el denominador

= (1 – cos A)/(√1 – cos ² A)

= $\sqrt\frac{(1-cosA)^2}{1-cos^2A}$

= $\sqrt\frac{(1-cosA)(1-cosA)}{(1-cosA)(1+cosA)}$

Paso 3

(1 – cos A) en el numerador y el denominador de la ecuación en el paso – 2 se cancela por lo que se convierte en,

= $\sqrt\frac{1-cosA}{1+cosA}$

= $\sqrt\frac{(1-\frac{1}{secA})}{1+\frac{1}{secA}}$

= $\sqrt\frac{secA-1}{secA+1}$

Del paso 3 se puede concluir que RHS = $\sqrt\frac{secA-1}{secA+1}$ que es igual a LHS y por lo tanto,

LHS = RHS

Por lo tanto Probado.

Problemas de muestra

Pregunta 1: Resuelve la identidad trigonométrica: $\sqrt{\frac{(sec A+1)}{(sec A-1)}*\frac{(1-cos A)}{(sin A)^2}}$

Solución:

Usando la identidad 2 y 3 para simplificar la identidad

= $\sqrt{\frac{(sec A+1)}{(sec A-1)}* (cosec A- cot A)^2}$

Ahora usando nuestra identidad derivada

= $\sqrt{\frac{1}{ (cosec A- cot A)^2)}* (cosec A- cot A)^2}$

⁼ √(1)

= 1

Pregunta 2: Resuelve la identidad trigonométrica: (cosec θ – cot θ) × 16 cot A/2

Solución:

Usando la identidad 4 para simplificar la identidad

= 16 × (cosec θ – cot θ) × (√((1+cos A)/(1-cos A))

Tomando cos A común en Numerador y Denominador en la raíz cuadrada y usando la identidad 8

= 16 × (cosec θ – cot θ) × √{(sec A+1)/(sec A- 1)

Usando la identidad probada anterior

= 16 × (cosec θ – cot θ) × 1/(cosec θ – cot θ)

= 16

Publicación traducida automáticamente

Artículo escrito por lokeshpotta20 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Funciones trigonométricas

Identidades trigonométricas

Pruebalo

Problemas de muestra

Deja una respuesta Cancelar la respuesta

Pruebalo $√\frac{sec θ - 1}{sec θ + 1} = cosec θ - cot θ$