Pregunta 1. Maximiza Z = 5x + 2y,
Sujeto a
3x + 5y ≤ 15
5x + 2y ≤ 10
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
3x + 5y = 15,
5x + 2y = 10,
x = 0 y
y = 0
Área representada por 3x + 5y ≤ 15:
La línea 3x + 5y = 15 conecta los ejes de coordenadas en A(5,0) y B(0,3) respectivamente.
Conectando estos puntos obtendremos la recta 3x + 5y = 15.
De este modo,
(0,0) asegura que en la ecuación 3x + 5y ≤ 15.
Por eso,
El área que tiene el origen muestra el conjunto solución de en la ecuación 3x + 5y ≤ 15.
El área muestra por 5x + 2y ≤ 10:
La línea 5x + 2y = 10 conecta los ejes de coordenadas en C(2,0) y D(0,5) respectivamente.
Conectando estos puntos obtendremos la recta 5x + 2y = 10.
De este modo,
(0,0) satisface la ecuación 5x + 2y ≤ 10.
Por eso,
El área que tiene el origen muestra el conjunto solución de en la ecuación 5x + 2y ≤ 10.
Área muestra por x ≥ 0 y y ≥ 0:
Aquí,
Todo el punto en el primer cuadrante asegura estos en ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones x ≥ 0 e y ≥ 0.
El área factible determinada por el sistema de restricciones, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0 e y ≥ 0, son las siguientes.
Los puntos de esquina del área factible son O(0, 0), C(2, 0), E
y B(0, 3).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 5 x + 3 y
O (0, 0)
5 × 0 + 3 × 0 = 0
C (2, 0)
5 × 2 + 3 × 0 = 10
mi
B (0, 3)
5 × 0 + 3 × 3 = 9
Por eso,
El valor máximo de Z
en el punto
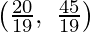
Por eso,
x=
e y =
es la mejor solución del LPP dado.
Por lo tanto,
El mejor valor de Z es
.
Pregunta 2. Maximizar Z = 9x + 3y
Sujeto a
2x + 3y ≤ 13
3x + y ≤ 5
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
2x + 3y = 13,
3x + y = 5,
x = 0 y
y = 0
Área mostrada por 2x + 3y ≤ 13:
La línea 2x + 3y = 13 conecta los ejes de coordenadas en A
y B
respectivamente.
Conectando estos puntos obtendremos la recta 2x + 3y = 13.
De este modo,
(0,0) asegura la ecuación de línea 2x + 3y ≤ 13.
Por lo tanto, el área que muestra el origen representa el conjunto solución de la ecuación 2x + 3y ≤ 13.
El área muestra por 3x + y ≤ 5:
La línea 5x + 2y = 10 conecta los ejes de coordenadas en C
y D(0, 5) respectivamente.
Después de conectar estos puntos,
Obtendremos la recta 3x + y = 5.
De este modo,
(0,0) asegura en la ecuación 3x + y ≤ 5.
De este modo,
El área que tiene el origen representa el conjunto solución de la ecuación 3x + y ≤ 5.
Área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todo el punto en el primer cuadrante asegura estos en ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones x ≥ 0 e y ≥ 0.
El área adecuada determinada por el sistema de restricciones,
2x + 3y ≤ 13,
3x + y ≤ 5,
x ≥ 0, y
y ≥ 0, son las siguientes.
Los puntos de las esquinas del área adecuada son O(0, 0), C
, E
y B
.
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 9 x + 3 y
O (0, 0)
9 × 0 + 3 × 0 = 0
C
9 ×
+ 3 × 0 = 15
mi
9 ×
+ 3 ×
= 15
B
9 × 0 + 3 ×
= 13
Aquí,
Podemos ver que el valor máximo de la función objetivo Z es 15 que está en C y
E.
De este modo,
El mejor valor de Z es 15.
Pregunta 3. Minimiza Z = 18x + 10y
Sujeto a
4x + y ≥ 20
2x + 3y ≥ 30
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
4x + y = 20,
2x +3y = 30,
x = 0 y
y = 0
Área mostrada por 4x + y ≥ 20 :
La línea 4x + y = 20 conecta los ejes de coordenadas en A(5, 0) y B(0, 20) respectivamente.
Conectando estos puntos obtendremos la recta 4x + y = 20.
De este modo,
(0,0) no asegura el en la ecuación 4x + y ≥ 20.
De este modo,
El área en el plano xy que no tiene origen representa el conjunto solución de la ecuación 4x + y ≥ 20.
Área mostrada por 2x +3y ≥ 30:
La línea 2x +3y = 30 conecta los ejes de coordenadas en C(15,0) y D(0, 10) respectivamente.
Uniendo estos puntos obtendremos la recta 2x+3y=30.
Así, (0,0) no asegura el en la ecuación 2x +3y ≥ 30.
De este modo,
El área que no tiene origen muestra el conjunto solución de en la ecuación 2x +3y ≥ 30.
Área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Cada punto en el primer cuadrante asegura esto en las ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones x ≥ 0 e y ≥ 0.
El área adecuada determinada por el sistema de restricciones, 4x + y ≥ 20, 2x +3y ≥ 30, x ≥ 0 e y ≥ 0, son las siguientes.
Los puntos de las esquinas del área adecuada son
b(0, 20),
C(15,0),
E(3,8) y
C(15,0).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 18 x + 10 y
B (0, 20)
18 × 0 + 10 × 20 = 200
mi (3,8)
18 × 3 + 10 × 8 = 134
C (15,0)
18 × 15 + 10 × 0 = 270
Por eso,
El valor mínimo de Z es 134 en el punto E(3,8). Por lo tanto, x = 3 ey = 8 es la mejor solución del LPP dado.
Por lo tanto,
El mejor valor de Z es 134.
Pregunta 4. Maximizar Z = 50x + 30y
Sujeto a
2x + y ≤ 18
3x + 2y ≤ 34
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
2x + y = 18, 3x + 2y = 34
El área mostrada por 2x + y ≥ 18:
La línea 2x + y = 18 conecta los ejes de coordenadas en A(9, 0) y B(0, 18) respectivamente.
Después de conectar estos puntos
Obtendremos la recta 2x + y = 18.
De este modo,
(0,0) no asegura el en la ecuación 2x + y ≥ 18.
De este modo,
La región en el plano xy que no tiene origen representa el conjunto solución de la ecuación 2x + y ≥ 18.
El área mostrada por 3x + 2y ≤ 34:
La línea 3x + 2y = 34 conecta los ejes de coordenadas en C
, 0 y D(0, 17) respectivamente.
Tras unir estos puntos obtendremos la recta 3x + 2y = 34.
De este modo,
(0,0) asegura que en la ecuación 3x + 2y ≤ 34.
De este modo,
El área que tiene el origen muestra el conjunto solución de en la ecuación 3x + 2y ≤ 34.
Los puntos de las esquinas del área adecuada son
A(9, 0), C
y E(2, 14).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 50 x + 30 y
un (9, 0)
50 × 9 + 3 × 0 = 450
C
50 ×
+ 30 × 0 =
E (2, 14)
50 × 2 + 30 × 14 = 520
Por eso,
El valor máximo de Z está
en el punto
.
Por eso,
x =
e y = 0 es la mejor solución del LPP dado.
Por lo tanto,
El mejor valor de Z es
Pregunta 5. Maximizar Z = 4x + 3y
Sujeto a
3x + 4y ≤ 24
8x + 6y ≤ 48
X ≤ 5
y ≤ 6
x, y ≥ 0
Solución:
Aquí tenemos que maximizar Z = 4x + 3y
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
3x + 4y = 24,
8x + 6y = 48,
x = 5,
y = 6,
x = 0 y
y = 0.
La línea 3x + 4y = 24 conecta el eje de coordenadas en A(8, 0) y B(0,6).
Conecta estos puntos para obtener la línea 3x + 4y = 24.
De este modo,
(0, 0) asegura que en la ecuación 3x + 4y ≤ 24.
De este modo,
El área en el plano xy que tiene el origen que muestra el conjunto solución de la ecuación dada.
La línea 8x + 6y = 48 conecta el eje de coordenadas en C(6, 0) y D(0,8). Conecta estos puntos para obtener la línea 8x + 6y = 48.
De este modo,
(0, 0) asegura que en la ecuación 8x + 6y ≤ 48.
De este modo,
El área en el plano xy que tiene el origen muestra el conjunto solución de la ecuación dada.
x = 5 es la recta que pasa por x = 5 paralela al eje Y.
y = 6 es la recta que pasa por y = 6 paralela al eje X.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todo el punto en el primer cuadrante asegura estos en ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones.
Estas líneas se dibujan utilizando una escala adecuada.
Los puntos de esquina del área adecuada son O(0, 0), G(5, 0), F
, E
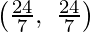
y B(0, 6).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 4 x + 3 y
O (0, 0)
4 × 0 + 3 × 0 = 0
G(5, 0)
4 × 5 + 3 × 0 = 20
F
4 × 5 + 3 ×
= 24
mi
4 ×
+ 3 ×
=
= 24
b(0, 6)
4 × 0 + 3 × 6 = 18
Aquí podemos ver que el valor máximo de la función objetivo Z es 24
Que está en F
y E
Por lo tanto,
El mejor valor de Z es 24.
Pregunta 6. Maximizar Z = 15x + 10y
Sujeto a
3x + 2y ≤ 80
2x + 3y ≤ 70
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
3x + 2y = 80, 2x + 3y = 70, x = 0 y y = 0
El área mostrada por 3x + 2y ≤ 80 :
La línea 3x + 2y = 80 conecta los ejes de coordenadas en A
, 0 y B(0, 40) respectivamente.
Conectando estos puntos obtendremos la recta 3x + 2y = 80.
De este modo,
(0,0) asegura que en la ecuación 3x + 2y ≤ 80 .
De este modo,
El área que tiene el origen representa el conjunto solución de la ecuación 3x + 2y ≤ 80 .
El área mostrada por 2x + 3y ≤ 70:
La línea 2x + 3y = 70 conecta los ejes de coordenadas en C(35, 0)C35, 0 y D(0, 703)D0, 703 respectivamente.
Después de conectar estos puntos obtendremos la línea 2x + 3y ≤ 70.
De este modo,
(0,0) asegura que en la ecuación 2x + 3y ≤ 70.
De este modo,
El área que tiene el origen muestra el conjunto solución de en la ecuación 2x + 3y ≤ 70.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Cada punto en el primer cuadrante asegura esto en las ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones, 3x + 2y ≤ 80, 2x + 3y ≤ 70, x ≥ 0 e y ≥ 0 son las siguientes.
Los puntos de las esquinas del área adecuada son O(0, 0), A
, 0 ,E(20, 10) y D
.
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 15 x + 10 y
O (0, 0)
15 × 0 + 10 × 0 = 0
A
15 ×
+ 10 × 0 = 400
E(20, 10)
15 × 20 + 10 × 10 = 400
D
15 × 0 + 10 ×
=
Así podemos ver que el valor máximo de la función objetivo Z es 400 que está en A
,
y E(20, 10).
Por lo tanto,
El mejor valor de Z es 400.
Pregunta 7. Maximiza Z = 10x + 6y
Sujeto a
3x + y ≤ 12
2x + 5y ≤ 34
x, y ≥ 0
Solución:
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
3x + y = 12, 2x + 5y = 34, x = 0 y y = 0
El área mostrada por 3x + y ≤ 12:
La línea 3x + y = 12 conecta los ejes de coordenadas en A(4, 0) y B(0, 12) respectivamente.
Después de conectar estos puntos obtendremos la línea 3x + y = 12.
De este modo,
(0,0) asegura la ecuación 3x + y ≤ 12.
De este modo,
El área que tiene el origen representa el conjunto solución de la ecuación 3x + y ≤ 12.
El área mostrada por 2x + 5y ≤ 34:
La línea 2x + 5y = 34 conecta los ejes de coordenadas en C(17, 0) y D
respectivamente.
Después de conectar estos puntos obtendremos la línea 2x + 5y ≤ 34.
De este modo,
(0,0) asegura que en la ecuación 2x + 5y ≤ 34.
De este modo,
El área que tiene el origen representa el conjunto solución de en la ecuación 2x + 5y ≤ 34.
Área que tiene por x ≥ 0 y y ≥ 0:
Por eso,
Todo el punto en el primer cuadrante asegura estos en ecuaciones.
De este modo,
El primer cuadrante es el área que muestran las ecuaciones x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones, 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0 e y ≥ 0 son las siguientes.
Los puntos de las esquinas del área adecuada son O(0, 0), A(4, 0), E(2, 6) y
D.
Los valores de Z en estos puntos de esquina son los siguientes:
punto de esquina
Z = 10 x + 6 y
O(0, 0)
10 × 0 + 6 × 0 = 0
A(4, 0)A4, 0
10 × 4 + 6 × 0 = 40
E(2, 6)E2, 6
10 × 2 + 6 × 6 = 56
D
10 × 0 + 6 ×
=
Aquí podemos ver que el valor máximo de la función objetivo Z es 56 que está en E(2, 6) eso significa en x = 2 y y = 6.
Por lo tanto,
El mejor valor de Z es 56.
Pregunta 8. Maximiza Z = 3x + 4y
Sujeto a
2x + 2y ≤ 80
2x + 4y ≤ 120
Solución:
Aquí tenemos que maximizar Z = 3x + 4y
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
2x + 2y = 80, 2x + 4y = 120
El área mostrada por 2x + 2y ≤ 80:
La línea 2x + 2y = 80 conecta los ejes de coordenadas en A(40, 0) y B(0, 40) respectivamente.
Después de conectar estos puntos obtendremos la línea 2x + 2y = 80.
De este modo,
(0,0) asegura que en la ecuación 2x + 2y ≤ 80.
De este modo,
El área que tiene el origen representa el conjunto solución de en la ecuación 2x + 2y ≤ 80.
El área mostrada por 2x + 4y ≤ 120:
La línea 2x + 4y = 120 conecta los ejes de coordenadas en C(60, 0) y D(0, 30) respectivamente.
Después de conectar estos puntos obtendremos la línea 2x + 4y ≤ 120.
De este modo,
(0,0) asegura que en la ecuación 2x + 4y ≤ 120.
De este modo,
El área que tiene el origen representa el conjunto solución de en la ecuación 2x + 4y ≤ 120.
El área adecuada determinada por el sistema de restricciones, 2x + 2y ≤ 80, 2x + 4y ≤ 120 son las siguientes:
Los puntos de esquina del área adecuada son O(0, 0), A(40, 0), E(20, 20) y D(0, 30).
Los valores de Z en estos puntos de esquina son los siguientes:
punto de esquina
Z = 3 x + 4 y
O (0, 0)
3 × 0 + 4 × 0 = 0
UN(40, 0)
3 × 40 + 4 × 0 = 120
E(20, 20)
3 × 20 + 4 × 20 = 140
D(0, 30)
10 × 0 + 4 × 30 = 120
Aquí podemos ver que el valor máximo de la función objetivo Z es 140 que está en E(20, 20) eso significa en
x = 20 y y = 20.
Por lo tanto,
El mejor valor de Z es 140.
Pregunta 9. Maximizar Z = 7x + 10y
Sujeto a
x + y ≤ 30000
y ≤ 12000
x ≥ 6000
x ≥ y
x, y ≥ 0
Solución:
Aquí tenemos que maximizar Z = 7x + 10y
Convertir lo dado en ecuaciones en ecuaciones,
Obtendremos las siguientes ecuaciones:
x + y = 30000, y = 12000, x = 6000, x = y, x = 0 y y = 0.
Región representada por x + y ≤ 30000:
La línea x + y = 30000 conecta los ejes de coordenadas en A(30000, 0) y B(0, 30000) respectivamente.
Después de conectar estos puntos obtendremos la línea x + y = 30000.
Así, (0,0) asegura en la ecuación x + y ≤ 30000.
De este modo,
el área que tiene el origen representa el conjunto solución de la ecuación x + y ≤ 30000.
La recta y = 12000 es la recta que pasa por C(0,12000) y paralela al eje x.
La recta x = 6000 es la recta que pasa por (6000, 0) y paralela al eje y.
El área mostrada por x ≥ y
La recta x = y es la recta que pasa por el origen. Los puntos a la derecha de la recta x = y aseguran la inecuación x ≥ y.
Como tomando el punto (−12000, 6000).
Aquí, 6000 > −12000 lo que implica y > x.
Por eso,
los puntos a la izquierda de la línea x = y no asegurarán la inecuación dada x ≥ y.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos del primer cuadrante aseguran estas inecuaciones.
De este modo,
el primer cuadrante es el área que muestran las inecuaciones x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones, x + y ≤ 30000, y ≤ 12000, x ≥ 6000, x ≥ y , x ≥ 0 e y ≥ 0 son las siguientes:
Los puntos de esquina de la región factible son
D(6000, 0),
A(3000,
F(18000, 12000) y
E(12000, 12000).
Los valores de Z en estos puntos de esquina son los siguientes:
punto de esquina
Z = 7 x + 10 y
D (6000, 0)
7 × 6000 + 10 × 0 = 42000
A(3000, 0)A3000, 0
7 × 3000 + 10 × 0 = 21000
F(18000, 12000)
7 × 18000 + 10 × 12000 = 246000
E(12000, 12000)
7 × 12000 + 10 × 12000 = 204000
Aquí podemos ver que el valor máximo de la función objetivo Z es 246000 que está en F(18000, 12000) eso significa en
x = 18000 y y = 12000.
Por lo tanto,
El mejor valor de Z es 246000.
Pregunta 10. Minimiza Z = 2x + 4y
Sujeto a
x + y ≥ 8
x + 4y ≥ 12
x ≥ 3, y ≥ 2
Solución:
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
x + y = 8, x + 4y = 12, x = 3, y = 2
El área muestra por x + y ≥ 8:
La línea x + y = 8 conecta los ejes de coordenadas en A(8, 0) y B(0, 8) respectivamente.
Después de conectar estos puntos obtendremos la línea x + y = 8.
De este modo,
(0,0) no asegura el en la ecuación x + y ≥ 8.
De este modo,
La región en el plano xy que no contiene el origen representa el conjunto solución de la ecuación x + y ≥ 8.
El área mostrada por x + 4y ≥ 12:
La línea x + 4y = 12 conecta los ejes de coordenadas en C(12, 0) y D(0, 3) respectivamente.
Después de conectar estos puntos obtendremos la línea x + 4y = 12.
De este modo,
(0,0) asegura que en la ecuación x + 4y ≥ 12.
De este modo,
el área en el plano xy que teniendo el origen representa el conjunto solución de la ecuación x + 4y ≥ 12.
La recta x = 3 es la recta que pasa por el punto (3, 0) y es paralela al eje Y.x ≥ 3 es el área a la derecha de la recta
x = 3.
La recta y = 2 es la recta que pasa por el punto (0, 12) y es paralela al eje X. y ≥ 2 es el área por encima de la recta y = 2.
Los puntos de esquina de la región adecuada son E(3, 5) y F(6, 2).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina Z = 2x + 4y
mi (3, 5)
2 × 3 + 4 × 5 = 26
F (6, 2)
2 × 6 + 4 × 2 = 20
Por lo tanto,
El valor mínimo de Z es 20 en el punto F(6, 2).
Por lo tanto, x = 6 ey = 2 es la mejor solución del LPP dado.
Por lo tanto,
El mejor valor de Z es 20.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA









