Pruebas de rutas básicas en pruebas de software

Requisito previo: base de prueba de ruta La prueba de ruta es una técnica de prueba de caja blanca basada en la estructura de control de un programa o módulo. Con esta estructura, se prepara un gráfico de flujo de control y se ejecutan las diversas rutas posibles presentes en el gráfico como parte de la prueba. Por lo tanto, por definición,

La prueba de ruta básica es una técnica de selección de rutas en el gráfico de flujo de control , que proporciona un conjunto básico de rutas de ejecución a través del programa o módulo.

Dado que esta prueba se basa en la estructura de control del programa, requiere un conocimiento completo de la estructura del programa. Para diseñar casos de prueba utilizando esta técnica, se siguen cuatro pasos:

1. Construya el gráfico de flujo de control
2. Calcule la complejidad ciclomática del gráfico
3. Identificar los caminos independientes
4. Diseño de casos de prueba a partir de rutas independientes

Entendamos cada paso uno por uno.

1. Gráfico de flujo de
control: un gráfico de flujo de control (o simplemente, gráfico de flujo) es un gráfico dirigido que representa la estructura de control de un programa o módulo. Un gráfico de flujo de control (V, E) tiene un número V de Nodes/vértices y un número E de aristas. Un gráfico de control también puede tener:

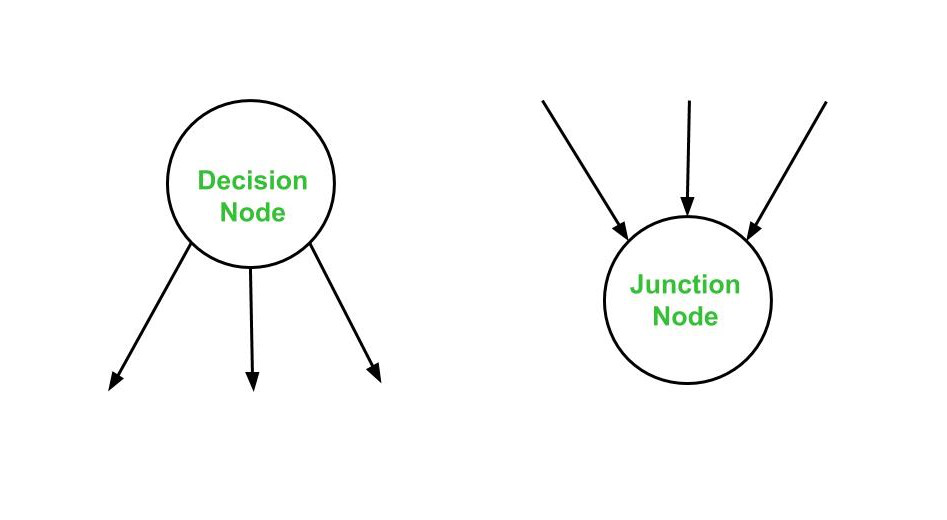
• Node de unión: un Node con más de una flecha entrando en él.
• Node de decisión: un Node con más de una flecha saliendo de él.
• Región: área delimitada por bordes y Nodes (el área fuera del gráfico también se cuenta como una región).

A continuación se muestran las notaciones utilizadas al construir un gráfico de flujo:

• Declaraciones Secuenciales –

  

• Si – Entonces – Si no –

  

• hacer – mientras –

  

• Mientras hace –

  

• Interruptor – Caja –

  

Complejidad
ciclomática: se dice que la complejidad ciclomática V (G) es una medida de la complejidad lógica de un programa. Se puede calcular mediante tres fórmulas diferentes:

1. Fórmula basada en aristas y Nodes:

   V(G) = e - n + 2*P

   Donde,
   e es el número de aristas,
   n es el número de vértices,
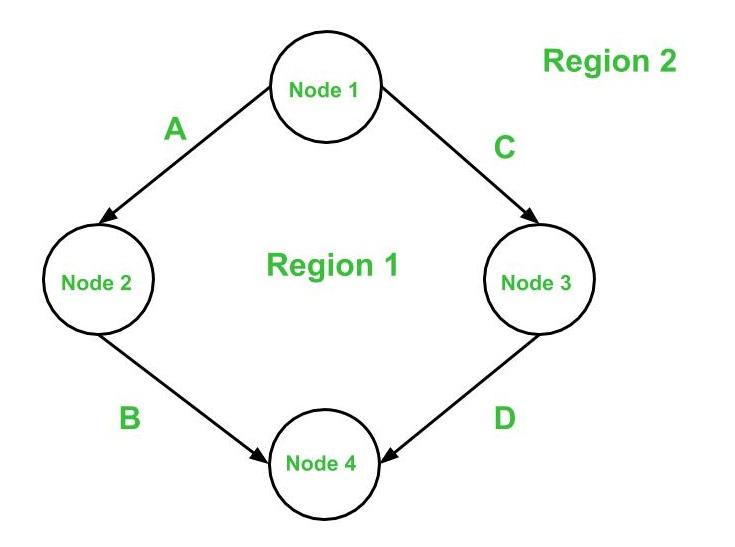
   P es el número de componentes conectados.

   Por ejemplo, considere el primer gráfico anterior,

   where, e = 4, n = 4 and p = 1 
   
   So,
   Cyclomatic complexity V(G) 
   = 4 - 4 + 2 * 1 
   = 2 

2. Fórmula basada en Nodes de decisión:

   V(G) = d + P 

   donde,
   d es el número de Nodes de decisión,
   P es el número de Nodes conectados.

   Por ejemplo, considere el primer gráfico anterior,

   where, d = 1 and p = 1
   
   So, 
   Cyclomatic Complexity V(G) 
   = 1 + 1 
   = 2 

3. Fórmula basada en regiones:

   V(G) = number of regions in the graph

   Por ejemplo, considere el primer gráfico anterior,

   Cyclomatic complexity V(G) 
   = 1 (for Region 1) + 1 (for Region 2)
   = 2 

Por lo tanto, utilizando las tres fórmulas anteriores, la complejidad ciclomática obtenida sigue siendo la misma. Todas estas tres fórmulas se pueden utilizar para calcular y verificar la complejidad ciclomática del gráfico de flujo.

Nota –

1. Para una función [por ejemplo, Principal( ) o Factorial( ) ], solo se construye un gráfico de flujo. Si en un programa hay múltiples funciones, entonces se construye un diagrama de flujo separado para cada una de ellas. Además, en la fórmula de complejidad ciclomática, el valor de ‘p’ se establece en función del número de grafos presentes en total.
2. Si un Node de decisión tiene exactamente dos flechas saliendo de él, entonces se cuenta como un Node de decisión. Sin embargo, si hay más de 2 flechas saliendo de un Node de decisión, se calcula usando esta fórmula:

   d = k - 1

   Aquí, k es el número de flechas que salen del Node de decisión.

Rutas Independientes:
Una ruta independiente en el gráfico de flujo de control es aquella que introduce al menos un nuevo borde que no ha sido atravesado antes de definir la ruta. La complejidad ciclomática da el número de caminos independientes presentes en un diagrama de flujo. Esto se debe a que la complejidad ciclomática se usa como un límite superior para el número de pruebas que deben ejecutarse para asegurarse de que todas las instrucciones del programa se hayan ejecutado al menos una vez.

Considere el primer gráfico dado arriba aquí, los caminos independientes serían 2 porque el número de caminos independientes es igual a la complejidad ciclomática.
Entonces, los caminos independientes en el primer gráfico dado arriba:

• Ruta 1:

  A -> B 

• Ruta 2:

  C -> D 

Nota:
las rutas independientes no son únicas. En otras palabras, si para un gráfico la complejidad ciclomática resulta ser N, entonces existe la posibilidad de obtener dos conjuntos diferentes de caminos que son de naturaleza independiente.

Diseñar casos de prueba:
Finalmente, después de obtener los caminos independientes, se pueden diseñar casos de prueba donde cada caso de prueba representa uno o más caminos independientes.

Ventajas :
Basis Path Testing puede ser aplicable en los siguientes casos:

1. Más cobertura:
   la prueba de ruta básica proporciona la mejor cobertura de código, ya que tiene como objetivo lograr la máxima cobertura lógica en lugar de la máxima cobertura de ruta. Esto da como resultado una prueba exhaustiva general del código.
2. Pruebas de mantenimiento:
   cuando se modifica un software, aún es necesario probar los cambios realizados en el software, lo que, como resultado, requiere pruebas de ruta.
3. Pruebas unitarias:
   cuando un desarrollador escribe el código, primero prueba la estructura del programa o módulo. Esta es la razón por la cual la prueba de ruta básica requiere suficiente conocimiento sobre la estructura del código.
4. Pruebas de integración:
   cuando un módulo llama a otros módulos, hay muchas posibilidades de errores de interfaz. Para evitar el caso de tales errores, se realizan pruebas de ruta para probar todas las rutas en las interfaces de los módulos.
5. Esfuerzo de prueba:
   dado que la técnica de prueba de ruta básica tiene en cuenta la complejidad del software (es decir, programa o módulo) al calcular la complejidad ciclomática, es intuitivo notar que el esfuerzo de prueba en el caso de la prueba de ruta básica es directamente proporcional a la complejidad del software o programa.