Requisito previo: gráfico de asignación de recursos (RAG) , algoritmo de banquero , programa para el algoritmo de banquero El algoritmo
de banquero es un algoritmo de asignación de recursos y evitación de puntos muertos. Este algoritmo prueba la seguridad simulando la asignación de cantidades posibles máximas predeterminadas de todos los recursos, luego realiza una verificación de «estado s» para probar posibles actividades, antes de decidir si se debe permitir que continúe la asignación.
En términos simples, verifica si la asignación de cualquier recurso conducirá a un punto muerto o no, O si es seguro asignar un recurso a un proceso y, de lo contrario, el recurso no se asigna a ese proceso. Determinar una secuencia segura (incluso si solo hay 1) garantizará que el sistema no entre en punto muerto.
El algoritmo de Banker se usa generalmente para encontrar si existe o no una secuencia segura. Pero aquí determinaremos el número total de secuencias seguras e imprimiremos todas las secuencias seguras.
La estructura de datos utilizada es:
- Vector disponible
- Array máxima
- Array de asignación
- Array de necesidades
Ejemplo:
Entrada:

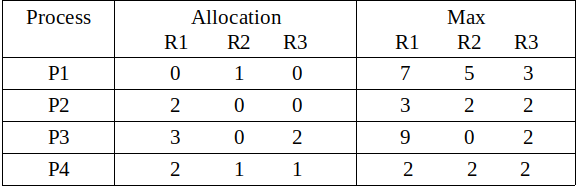
Output: Safe sequences are: P2--> P4--> P1--> P3 P2--> P4--> P3--> P1 P4--> P2--> P1--> P3 P4--> P2--> P3--> P1 There are total 4 safe-sequences
Explicación:
los recursos totales son R1 = 10, R2 = 5, R3 = 7 y los recursos asignados son R1 = (0+2+3+2 =) 7, R2 = (1+0+0+1 =) 2, R3 = (0+0+2+1 =) 3. Por lo tanto, los recursos restantes son R1 = (10 – 7 =) 3, R2 = (5 – 2 =) 3, R3 = (7 – 3 =) 4.
Quedan disponibles = Recursos totales: recursos asignados
y
necesidad restante = máx.: asignado
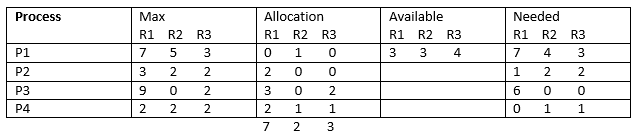
Entonces, podemos comenzar desde P2 o P4. No podemos satisfacer la necesidad restante de los recursos disponibles de P1 o P3 en el paso de primer o segundo intento del algoritmo de Banker. Solo hay cuatro posibles secuencias seguras. Estos son:
P2–> P4–> P1–> P3
P2–> P4–> P3–> P1
P4–> P2–> P1–> P3
P4–> P2–> P3–> P1
Implementación:
C++
// C++ Program to Print all possible safe sequences using banker's algorithm
#include <iostream>
#include <string.h>
#include <vector>
// total number of process
#define P 4
// total number of resources
#define R 3
// total safe-sequences
int total = 0;
using namespace std;
// function to check if process
// can be allocated or not
bool is_available(int process_id, int allocated[][R],
int max[][R], int need[][R], int available[])
{
bool flag = true;
// check if all the available resources
// are less greater than need of process
for (int i = 0; i < R; i++) {
if (need[process_id][i] > available[i])
flag = false;
}
return flag;
}
// Print all the safe-sequences
void safe_sequence(bool marked[], int allocated[][R], int max[][R],
int need[][R], int available[], vector<int> safe)
{
for (int i = 0; i < P; i++) {
// check if it is not marked
// already and can be allocated
if (!marked[i] && is_available(i, allocated, max, need, available)) {
// mark the process
marked[i] = true;
// increase the available
// by deallocating from process i
for (int j = 0; j < R; j++)
available[j] += allocated[i][j];
safe.push_back(i);
// find safe sequence by taking process i
safe_sequence(marked, allocated, max, need, available, safe);
safe.pop_back();
// unmark the process
marked[i] = false;
// decrease the available
for (int j = 0; j < R; j++)
available[j] -= allocated[i][j];
}
}
// if a safe-sequence is found, display it
if (safe.size() == P) {
total++;
for (int i = 0; i < P; i++) {
cout << "P" << safe[i] + 1;
if (i != (P - 1))
cout << "--> ";
}
cout << endl;
}
}
// Driver Code
int main()
{
// allocated matrix of size P*R
int allocated[P][R] = { { 0, 1, 0 },
{ 2, 0, 0 },
{ 3, 0, 2 },
{ 2, 1, 1 } };
// max matrix of size P*R
int max[P][R] = { { 7, 5, 3 },
{ 3, 2, 2 },
{ 9, 0, 2 },
{ 2, 2, 2 } };
// Initial total resources
int resources[R] = { 10, 5, 7 };
// available vector of size R
int available[R];
for (int i = 0; i < R; i++) {
int sum = 0;
for (int j = 0; j < P; j++)
sum += allocated[j][i];
available[i] = resources[i] - sum;
}
// safe vector for displaying a safe-sequence
vector<int> safe;
// marked of size P for marking allocated process
bool marked[P];
memset(marked, false, sizeof(marked));
// need matrix of size P*R
int need[P][R];
for (int i = 0; i < P; i++)
for (int j = 0; j < R; j++)
need[i][j] = max[i][j] - allocated[i][j];
cout << "Safe sequences are:" << endl;
safe_sequence(marked, allocated, max, need, available, safe);
cout << "\nThere are total " << total << " safe-sequences" << endl;
return 0;
}
Java
// Java Program to Print all possible safe
// sequences using banker's algorithm
import java.util.*;
public class GFG
{
// total number of process
static int P = 4;
// total number of resources
static int R = 3;
// total safe-sequences
static int total = 0;
// function to check if process
// can be allocated or not
static boolean is_available(int process_id, int allocated[][],
int max[][], int need[][], int available[])
{
boolean flag = true;
// check if all the available resources
// are less greater than need of process
for (int i = 0; i < R; i++)
{
if (need[process_id][i] > available[i])
{
flag = false;
}
}
return flag;
}
// Print all the safe-sequences
static void safe_sequence(boolean marked[], int allocated[][], int max[][],
int need[][], int available[], Vector<Integer> safe)
{
for (int i = 0; i < P; i++)
{
// check if it is not marked
// already and can be allocated
if (!marked[i] && is_available(i, allocated, max, need, available))
{
// mark the process
marked[i] = true;
// increase the available
// by deallocating from process i
for (int j = 0; j < R; j++)
{
available[j] += allocated[i][j];
}
safe.add(i);
// find safe sequence by taking process i
safe_sequence(marked, allocated, max, need, available, safe);
safe.removeElementAt(safe.size() - 1);
// unmark the process
marked[i] = false;
// decrease the available
for (int j = 0; j < R; j++)
{
available[j] -= allocated[i][j];
}
}
}
// if a safe-sequence is found, display it
if (safe.size() == P)
{
total++;
for (int i = 0; i < P; i++)
{
System.out.print("P" + (safe.get(i) + 1));
if (i != (P - 1))
{
System.out.print("--> ");
}
}
System.out.println("");;
}
}
// Driver Code
public static void main(String[] args)
{
// allocated matrix of size P*R
int allocated[][] = {{0, 1, 0},
{2, 0, 0},
{3, 0, 2},
{2, 1, 1}};
// max matrix of size P*R
int max[][] = {{7, 5, 3},
{3, 2, 2},
{9, 0, 2},
{2, 2, 2}};
// Initial total resources
int resources[] = {10, 5, 7};
// available vector of size R
int[] available = new int[R];
for (int i = 0; i < R; i++)
{
int sum = 0;
for (int j = 0; j < P; j++)
{
sum += allocated[j][i];
}
available[i] = resources[i] - sum;
}
// safe vector for displaying a safe-sequence
Vector<Integer> safe = new Vector<Integer>();
// marked of size P for marking allocated process
boolean[] marked = new boolean[P];
// need matrix of size P*R
int[][] need = new int[P][R];
for (int i = 0; i < P; i++)
{
for (int j = 0; j < R; j++)
{
need[i][j] = max[i][j] - allocated[i][j];
}
}
System.out.println("Safe sequences are:");
safe_sequence(marked, allocated, max, need, available, safe);
System.out.println("\nThere are total " + total + " safe-sequences");
}
}
/* This code contributed by PrinciRaj1992 */
Python3
# Python3 program to print all
# possible safe sequences
# using banker's algorithm
# Total number of process
P = 4
# Total number of resources
R = 3
# Total safe-sequences
total = 0
# Function to check if process
# can be allocated or not
def is_available(process_id, allocated,
max, need, available):
flag = True
# Check if all the available resources
# are less greater than need of process
for i in range(R):
if (need[process_id][i] > available[i]):
flag = False
return flag
# Print all the safe-sequences
def safe_sequence(marked, allocated,
max, need, available, safe):
global total, P, R
for i in range(P):
# Check if it is not marked
# already and can be allocated
if (not marked[i] and
is_available(i, allocated, max,
need, available)):
# mark the process
marked[i] = True
# Increase the available
# by deallocating from process i
for j in range(R):
available[j] += allocated[i][j]
safe.append(i)
# Find safe sequence by taking process i
safe_sequence(marked, allocated, max,
need, available, safe)
safe.pop()
# unmark the process
marked[i] = False
# Decrease the available
for j in range(R):
available[j] -= allocated[i][j]
# If a safe-sequence is found, display it
if (len(safe) == P):
total += 1
for i in range(P):
print("P" + str(safe[i] + 1), end = '')
if (i != (P - 1)):
print("--> ", end = '')
print()
# Driver code
if __name__=="__main__":
# Allocated matrix of size P*R
allocated = [ [ 0, 1, 0 ],
[ 2, 0, 0 ],
[ 3, 0, 2 ],
[ 2, 1, 1 ]]
# max matrix of size P*R
max = [ [ 7, 5, 3 ],
[ 3, 2, 2 ],
[ 9, 0, 2 ],
[ 2, 2, 2 ] ]
# Initial total resources
resources = [ 10, 5, 7 ]
# Available vector of size R
available = [0 for i in range(R)]
for i in range(R):
sum = 0
for j in range(P):
sum += allocated[j][i]
available[i] = resources[i] - sum
# Safe vector for displaying a
# safe-sequence
safe = []
# Marked of size P for marking
# allocated process
marked = [False for i in range(P)]
# Need matrix of size P*R
need = [[0 for j in range(R)]
for i in range(P)]
for i in range(P):
for j in range(R):
need[i][j] = (max[i][j] -
allocated[i][j])
print("Safe sequences are:")
safe_sequence(marked, allocated, max,
need, available, safe)
print("\nThere are total " + str(total) +
" safe-sequences")
# This code is contributed by rutvik_56
C#
// C# Program to Print all possible safe
// sequences using banker's algorithm
using System;
using System.Collections.Generic;
class GFG
{
// total number of process
static int P = 4;
// total number of resources
static int R = 3;
// total safe-sequences
static int total = 0;
// function to check if process
// can be allocated or not
static Boolean is_available(int process_id,
int [,]allocated,
int [,]max, int [,]need,
int []available)
{
Boolean flag = true;
// check if all the available resources
// are less greater than need of process
for (int i = 0; i < R; i++)
{
if (need[process_id, i] > available[i])
{
flag = false;
}
}
return flag;
}
// Print all the safe-sequences
static void safe_sequence(Boolean []marked,
int [,]allocated,
int [,]max, int [,]need,
int []available,
List<int> safe)
{
for (int i = 0; i < P; i++)
{
// check if it is not marked
// already and can be allocated
if (!marked[i] &&
is_available(i, allocated, max,
need, available))
{
// mark the process
marked[i] = true;
// increase the available
// by deallocating from process i
for (int j = 0; j < R; j++)
{
available[j] += allocated[i, j];
}
safe.Add(i);
// find safe sequence by taking process i
safe_sequence(marked, allocated, max,
need, available, safe);
safe.RemoveAt(safe.Count - 1);
// unmark the process
marked[i] = false;
// decrease the available
for (int j = 0; j < R; j++)
{
available[j] -= allocated[i, j];
}
}
}
// if a safe-sequence is found,
// display it
if (safe.Count == P)
{
total++;
for (int i = 0; i < P; i++)
{
Console.Write("P" + (safe[i] + 1));
if (i != (P - 1))
{
Console.Write("--> ");
}
}
Console.WriteLine("");;
}
}
// Driver Code
public static void Main(String[] args)
{
// allocated matrix of size P*R
int [,]allocated = {{0, 1, 0},
{2, 0, 0},
{3, 0, 2},
{2, 1, 1}};
// max matrix of size P*R
int [,]max = {{7, 5, 3},
{3, 2, 2},
{9, 0, 2},
{2, 2, 2}};
// Initial total resources
int []resources = {10, 5, 7};
// available vector of size R
int[] available = new int[R];
for (int i = 0; i < R; i++)
{
int sum = 0;
for (int j = 0; j < P; j++)
{
sum += allocated[j,i];
}
available[i] = resources[i] - sum;
}
// safe vector for displaying a safe-sequence
List<int> safe = new List<int>();
// marked of size P for marking
// allocated process
Boolean[] marked = new Boolean[P];
// need matrix of size P*R
int[,] need = new int[P, R];
for (int i = 0; i < P; i++)
{
for (int j = 0; j < R; j++)
{
need[i, j] = max[i, j] - allocated[i, j];
}
}
Console.WriteLine("Safe sequences are:");
safe_sequence(marked, allocated, max,
need, available, safe);
Console.WriteLine("\nThere are total " +
total + " safe-sequences");
}
}
// This code is contributed by Rajput-Ji
Producción:
Safe sequences are: P2--> P4--> P1--> P3 P2--> P4--> P3--> P1 P4--> P2--> P1--> P3 P4--> P2--> P3--> P1 There are total 4 safe-sequences
Publicación traducida automáticamente
Artículo escrito por shubham_rana_77 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA