Motivación
Para aproximar el camino más corto en situaciones de la vida real, como en mapas, juegos donde puede haber muchos obstáculos.
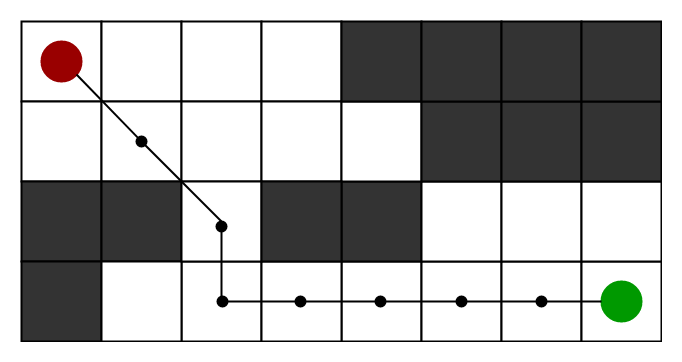
Podemos considerar una cuadrícula 2D que tiene varios obstáculos y comenzamos desde una celda de origen (de color rojo a continuación) para llegar a una celda de destino (de color verde a continuación)
C++
// A C++ Program to implement A* Search Algorithm
#include <bits/stdc++.h>
using namespace std;
#define ROW 9
#define COL 10
// Creating a shortcut for int, int pair type
typedef pair<int, int> Pair;
// Creating a shortcut for pair<int, pair<int, int>> type
typedef pair<double, pair<int, int> > pPair;
// A structure to hold the necessary parameters
struct cell {
// Row and Column index of its parent
// Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
int parent_i, parent_j;
// f = g + h
double f, g, h;
};
// A Utility Function to check whether given cell (row, col)
// is a valid cell or not.
bool isValid(int row, int col)
{
// Returns true if row number and column number
// is in range
return (row >= 0) && (row < ROW) && (col >= 0)
&& (col < COL);
}
// A Utility Function to check whether the given cell is
// blocked or not
bool isUnBlocked(int grid[][COL], int row, int col)
{
// Returns true if the cell is not blocked else false
if (grid[row][col] == 1)
return (true);
else
return (false);
}
// A Utility Function to check whether destination cell has
// been reached or not
bool isDestination(int row, int col, Pair dest)
{
if (row == dest.first && col == dest.second)
return (true);
else
return (false);
}
// A Utility Function to calculate the 'h' heuristics.
double calculateHValue(int row, int col, Pair dest)
{
// Return using the distance formula
return ((double)sqrt(
(row - dest.first) * (row - dest.first)
+ (col - dest.second) * (col - dest.second)));
}
// A Utility Function to trace the path from the source
// to destination
void tracePath(cell cellDetails[][COL], Pair dest)
{
printf("\nThe Path is ");
int row = dest.first;
int col = dest.second;
stack<Pair> Path;
while (!(cellDetails[row][col].parent_i == row
&& cellDetails[row][col].parent_j == col)) {
Path.push(make_pair(row, col));
int temp_row = cellDetails[row][col].parent_i;
int temp_col = cellDetails[row][col].parent_j;
row = temp_row;
col = temp_col;
}
Path.push(make_pair(row, col));
while (!Path.empty()) {
pair<int, int> p = Path.top();
Path.pop();
printf("-> (%d,%d) ", p.first, p.second);
}
return;
}
// A Function to find the shortest path between
// a given source cell to a destination cell according
// to A* Search Algorithm
void aStarSearch(int grid[][COL], Pair src, Pair dest)
{
// If the source is out of range
if (isValid(src.first, src.second) == false) {
printf("Source is invalid\n");
return;
}
// If the destination is out of range
if (isValid(dest.first, dest.second) == false) {
printf("Destination is invalid\n");
return;
}
// Either the source or the destination is blocked
if (isUnBlocked(grid, src.first, src.second) == false
|| isUnBlocked(grid, dest.first, dest.second)
== false) {
printf("Source or the destination is blocked\n");
return;
}
// If the destination cell is the same as source cell
if (isDestination(src.first, src.second, dest)
== true) {
printf("We are already at the destination\n");
return;
}
// Create a closed list and initialise it to false which
// means that no cell has been included yet This closed
// list is implemented as a boolean 2D array
bool closedList[ROW][COL];
memset(closedList, false, sizeof(closedList));
// Declare a 2D array of structure to hold the details
// of that cell
cell cellDetails[ROW][COL];
int i, j;
for (i = 0; i < ROW; i++) {
for (j = 0; j < COL; j++) {
cellDetails[i][j].f = FLT_MAX;
cellDetails[i][j].g = FLT_MAX;
cellDetails[i][j].h = FLT_MAX;
cellDetails[i][j].parent_i = -1;
cellDetails[i][j].parent_j = -1;
}
}
// Initialising the parameters of the starting node
i = src.first, j = src.second;
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent_i = i;
cellDetails[i][j].parent_j = j;
/*
Create an open list having information as-
<f, <i, j>>
where f = g + h,
and i, j are the row and column index of that cell
Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
This open list is implemented as a set of pair of
pair.*/
set<pPair> openList;
// Put the starting cell on the open list and set its
// 'f' as 0
openList.insert(make_pair(0.0, make_pair(i, j)));
// We set this boolean value as false as initially
// the destination is not reached.
bool foundDest = false;
while (!openList.empty()) {
pPair p = *openList.begin();
// Remove this vertex from the open list
openList.erase(openList.begin());
// Add this vertex to the closed list
i = p.second.first;
j = p.second.second;
closedList[i][j] = true;
/*
Generating all the 8 successor of this cell
N.W N N.E
\ | /
\ | /
W----Cell----E
/ | \
/ | \
S.W S S.E
Cell-->Popped Cell (i, j)
N --> North (i-1, j)
S --> South (i+1, j)
E --> East (i, j+1)
W --> West (i, j-1)
N.E--> North-East (i-1, j+1)
N.W--> North-West (i-1, j-1)
S.E--> South-East (i+1, j+1)
S.W--> South-West (i+1, j-1)*/
// To store the 'g', 'h' and 'f' of the 8 successors
double gNew, hNew, fNew;
//----------- 1st Successor (North) ------------
// Only process this cell if this is a valid one
if (isValid(i - 1, j) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i - 1, j, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i - 1][j].parent_i = i;
cellDetails[i - 1][j].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i - 1][j] == false
&& isUnBlocked(grid, i - 1, j)
== true) {
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(i - 1, j, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i - 1][j].f == FLT_MAX
|| cellDetails[i - 1][j].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i - 1, j)));
// Update the details of this cell
cellDetails[i - 1][j].f = fNew;
cellDetails[i - 1][j].g = gNew;
cellDetails[i - 1][j].h = hNew;
cellDetails[i - 1][j].parent_i = i;
cellDetails[i - 1][j].parent_j = j;
}
}
}
//----------- 2nd Successor (South) ------------
// Only process this cell if this is a valid one
if (isValid(i + 1, j) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i + 1, j, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i + 1][j].parent_i = i;
cellDetails[i + 1][j].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i + 1][j] == false
&& isUnBlocked(grid, i + 1, j)
== true) {
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(i + 1, j, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i + 1][j].f == FLT_MAX
|| cellDetails[i + 1][j].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i + 1, j)));
// Update the details of this cell
cellDetails[i + 1][j].f = fNew;
cellDetails[i + 1][j].g = gNew;
cellDetails[i + 1][j].h = hNew;
cellDetails[i + 1][j].parent_i = i;
cellDetails[i + 1][j].parent_j = j;
}
}
}
//----------- 3rd Successor (East) ------------
// Only process this cell if this is a valid one
if (isValid(i, j + 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i, j + 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i][j + 1].parent_i = i;
cellDetails[i][j + 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i][j + 1] == false
&& isUnBlocked(grid, i, j + 1)
== true) {
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(i, j + 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i][j + 1].f == FLT_MAX
|| cellDetails[i][j + 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i, j + 1)));
// Update the details of this cell
cellDetails[i][j + 1].f = fNew;
cellDetails[i][j + 1].g = gNew;
cellDetails[i][j + 1].h = hNew;
cellDetails[i][j + 1].parent_i = i;
cellDetails[i][j + 1].parent_j = j;
}
}
}
//----------- 4th Successor (West) ------------
// Only process this cell if this is a valid one
if (isValid(i, j - 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i, j - 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i][j - 1].parent_i = i;
cellDetails[i][j - 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i][j - 1] == false
&& isUnBlocked(grid, i, j - 1)
== true) {
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(i, j - 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i][j - 1].f == FLT_MAX
|| cellDetails[i][j - 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i, j - 1)));
// Update the details of this cell
cellDetails[i][j - 1].f = fNew;
cellDetails[i][j - 1].g = gNew;
cellDetails[i][j - 1].h = hNew;
cellDetails[i][j - 1].parent_i = i;
cellDetails[i][j - 1].parent_j = j;
}
}
}
//----------- 5th Successor (North-East)
//------------
// Only process this cell if this is a valid one
if (isValid(i - 1, j + 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i - 1, j + 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i - 1][j + 1].parent_i = i;
cellDetails[i - 1][j + 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i - 1][j + 1] == false
&& isUnBlocked(grid, i - 1, j + 1)
== true) {
gNew = cellDetails[i][j].g + 1.414;
hNew = calculateHValue(i - 1, j + 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i - 1][j + 1].f == FLT_MAX
|| cellDetails[i - 1][j + 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i - 1, j + 1)));
// Update the details of this cell
cellDetails[i - 1][j + 1].f = fNew;
cellDetails[i - 1][j + 1].g = gNew;
cellDetails[i - 1][j + 1].h = hNew;
cellDetails[i - 1][j + 1].parent_i = i;
cellDetails[i - 1][j + 1].parent_j = j;
}
}
}
//----------- 6th Successor (North-West)
//------------
// Only process this cell if this is a valid one
if (isValid(i - 1, j - 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i - 1, j - 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i - 1][j - 1].parent_i = i;
cellDetails[i - 1][j - 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i - 1][j - 1] == false
&& isUnBlocked(grid, i - 1, j - 1)
== true) {
gNew = cellDetails[i][j].g + 1.414;
hNew = calculateHValue(i - 1, j - 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i - 1][j - 1].f == FLT_MAX
|| cellDetails[i - 1][j - 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i - 1, j - 1)));
// Update the details of this cell
cellDetails[i - 1][j - 1].f = fNew;
cellDetails[i - 1][j - 1].g = gNew;
cellDetails[i - 1][j - 1].h = hNew;
cellDetails[i - 1][j - 1].parent_i = i;
cellDetails[i - 1][j - 1].parent_j = j;
}
}
}
//----------- 7th Successor (South-East)
//------------
// Only process this cell if this is a valid one
if (isValid(i + 1, j + 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i + 1, j + 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i + 1][j + 1].parent_i = i;
cellDetails[i + 1][j + 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i + 1][j + 1] == false
&& isUnBlocked(grid, i + 1, j + 1)
== true) {
gNew = cellDetails[i][j].g + 1.414;
hNew = calculateHValue(i + 1, j + 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i + 1][j + 1].f == FLT_MAX
|| cellDetails[i + 1][j + 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i + 1, j + 1)));
// Update the details of this cell
cellDetails[i + 1][j + 1].f = fNew;
cellDetails[i + 1][j + 1].g = gNew;
cellDetails[i + 1][j + 1].h = hNew;
cellDetails[i + 1][j + 1].parent_i = i;
cellDetails[i + 1][j + 1].parent_j = j;
}
}
}
//----------- 8th Successor (South-West)
//------------
// Only process this cell if this is a valid one
if (isValid(i + 1, j - 1) == true) {
// If the destination cell is the same as the
// current successor
if (isDestination(i + 1, j - 1, dest) == true) {
// Set the Parent of the destination cell
cellDetails[i + 1][j - 1].parent_i = i;
cellDetails[i + 1][j - 1].parent_j = j;
printf("The destination cell is found\n");
tracePath(cellDetails, dest);
foundDest = true;
return;
}
// If the successor is already on the closed
// list or if it is blocked, then ignore it.
// Else do the following
else if (closedList[i + 1][j - 1] == false
&& isUnBlocked(grid, i + 1, j - 1)
== true) {
gNew = cellDetails[i][j].g + 1.414;
hNew = calculateHValue(i + 1, j - 1, dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add it to
// the open list. Make the current square
// the parent of this square. Record the
// f, g, and h costs of the square cell
// OR
// If it is on the open list already, check
// to see if this path to that square is
// better, using 'f' cost as the measure.
if (cellDetails[i + 1][j - 1].f == FLT_MAX
|| cellDetails[i + 1][j - 1].f > fNew) {
openList.insert(make_pair(
fNew, make_pair(i + 1, j - 1)));
// Update the details of this cell
cellDetails[i + 1][j - 1].f = fNew;
cellDetails[i + 1][j - 1].g = gNew;
cellDetails[i + 1][j - 1].h = hNew;
cellDetails[i + 1][j - 1].parent_i = i;
cellDetails[i + 1][j - 1].parent_j = j;
}
}
}
}
// When the destination cell is not found and the open
// list is empty, then we conclude that we failed to
// reach the destination cell. This may happen when the
// there is no way to destination cell (due to
// blockages)
if (foundDest == false)
printf("Failed to find the Destination Cell\n");
return;
}
// Driver program to test above function
int main()
{
/* Description of the Grid-
1--> The cell is not blocked
0--> The cell is blocked */
int grid[ROW][COL]
= { { 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 },
{ 1, 1, 1, 0, 1, 1, 1, 0, 1, 1 },
{ 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 1, 0, 0, 0, 0, 1 },
{ 1, 1, 1, 0, 1, 1, 1, 0, 1, 0 },
{ 1, 0, 1, 1, 1, 1, 0, 1, 0, 0 },
{ 1, 0, 0, 0, 0, 1, 0, 0, 0, 1 },
{ 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 },
{ 1, 1, 1, 0, 0, 0, 1, 0, 0, 1 } };
// Source is the left-most bottom-most corner
Pair src = make_pair(8, 0);
// Destination is the left-most top-most corner
Pair dest = make_pair(0, 0);
aStarSearch(grid, src, dest);
return (0);
}
C++14
// A C++ Program to implement A* Search Algorithm
#include "math.h"
#include <array>
#include <chrono>
#include <cstring>
#include <iostream>
#include <queue>
#include <set>
#include <stack>
#include <tuple>
using namespace std;
// Creating a shortcut for int, int pair type
typedef pair<int, int> Pair;
// Creating a shortcut for tuple<int, int, int> type
typedef tuple<double, int, int> Tuple;
// A structure to hold the necessary parameters
struct cell {
// Row and Column index of its parent
Pair parent;
// f = g + h
double f, g, h;
cell()
: parent(-1, -1)
, f(-1)
, g(-1)
, h(-1)
{
}
};
// A Utility Function to check whether given cell (row, col)
// is a valid cell or not.
template <size_t ROW, size_t COL>
bool isValid(const array<array<int, COL>, ROW>& grid,
const Pair& point)
{ // Returns true if row number and column number is in
// range
if (ROW > 0 && COL > 0)
return (point.first >= 0) && (point.first < ROW)
&& (point.second >= 0)
&& (point.second < COL);
return false;
}
// A Utility Function to check whether the given cell is
// blocked or not
template <size_t ROW, size_t COL>
bool isUnBlocked(const array<array<int, COL>, ROW>& grid,
const Pair& point)
{
// Returns true if the cell is not blocked else false
return isValid(grid, point)
&& grid[point.first][point.second] == 1;
}
// A Utility Function to check whether destination cell has
// been reached or not
bool isDestination(const Pair& position, const Pair& dest)
{
return position == dest;
}
// A Utility Function to calculate the 'h' heuristics.
double calculateHValue(const Pair& src, const Pair& dest)
{
// h is estimated with the two points distance formula
return sqrt(pow((src.first - dest.first), 2.0)
+ pow((src.second - dest.second), 2.0));
}
// A Utility Function to trace the path from the source to
// destination
template <size_t ROW, size_t COL>
void tracePath(
const array<array<cell, COL>, ROW>& cellDetails,
const Pair& dest)
{
printf("\nThe Path is ");
stack<Pair> Path;
int row = dest.first;
int col = dest.second;
Pair next_node = cellDetails[row][col].parent;
do {
Path.push(next_node);
next_node = cellDetails[row][col].parent;
row = next_node.first;
col = next_node.second;
} while (cellDetails[row][col].parent != next_node);
Path.emplace(row, col);
while (!Path.empty()) {
Pair p = Path.top();
Path.pop();
printf("-> (%d,%d) ", p.first, p.second);
}
}
// A Function to find the shortest path between a given
// source cell to a destination cell according to A* Search
// Algorithm
template <size_t ROW, size_t COL>
void aStarSearch(const array<array<int, COL>, ROW>& grid,
const Pair& src, const Pair& dest)
{
// If the source is out of range
if (!isValid(grid, src)) {
printf("Source is invalid\n");
return;
}
// If the destination is out of range
if (!isValid(grid, dest)) {
printf("Destination is invalid\n");
return;
}
// Either the source or the destination is blocked
if (!isUnBlocked(grid, src)
|| !isUnBlocked(grid, dest)) {
printf("Source or the destination is blocked\n");
return;
}
// If the destination cell is the same as source cell
if (isDestination(src, dest)) {
printf("We are already at the destination\n");
return;
}
// Create a closed list and initialise it to false which
// means that no cell has been included yet This closed
// list is implemented as a boolean 2D array
bool closedList[ROW][COL];
memset(closedList, false, sizeof(closedList));
// Declare a 2D array of structure to hold the details
// of that cell
array<array<cell, COL>, ROW> cellDetails;
int i, j;
// Initialising the parameters of the starting node
i = src.first, j = src.second;
cellDetails[i][j].f = 0.0;
cellDetails[i][j].g = 0.0;
cellDetails[i][j].h = 0.0;
cellDetails[i][j].parent = { i, j };
/*
Create an open list having information as-
<f, <i, j>>
where f = g + h,
and i, j are the row and column index of that cell
Note that 0 <= i <= ROW-1 & 0 <= j <= COL-1
This open list is implemented as a set of tuple.*/
std::priority_queue<Tuple, std::vector<Tuple>,
std::greater<Tuple> >
openList;
// Put the starting cell on the open list and set its
// 'f' as 0
openList.emplace(0.0, i, j);
// We set this boolean value as false as initially
// the destination is not reached.
while (!openList.empty()) {
const Tuple& p = openList.top();
// Add this vertex to the closed list
i = get<1>(p); // second element of tuple
j = get<2>(p); // third element of tuple
// Remove this vertex from the open list
openList.pop();
closedList[i][j] = true;
/*
Generating all the 8 successor of this cell
N.W N N.E
\ | /
\ | /
W----Cell----E
/ | \
/ | \
S.W S S.E
Cell-->Popped Cell (i, j)
N --> North (i-1, j)
S --> South (i+1, j)
E --> East (i, j+1)
W --> West (i, j-1)
N.E--> North-East (i-1, j+1)
N.W--> North-West (i-1, j-1)
S.E--> South-East (i+1, j+1)
S.W--> South-West (i+1, j-1)
*/
for (int add_x = -1; add_x <= 1; add_x++) {
for (int add_y = -1; add_y <= 1; add_y++) {
Pair neighbour(i + add_x, j + add_y);
// Only process this cell if this is a valid
// one
if (isValid(grid, neighbour)) {
// If the destination cell is the same
// as the current successor
if (isDestination(
neighbour,
dest)) { // Set the Parent of
// the destination cell
cellDetails[neighbour.first]
[neighbour.second]
.parent
= { i, j };
printf("The destination cell is "
"found\n");
tracePath(cellDetails, dest);
return;
}
// If the successor is already on the
// closed list or if it is blocked, then
// ignore it. Else do the following
else if (!closedList[neighbour.first]
[neighbour.second]
&& isUnBlocked(grid,
neighbour)) {
double gNew, hNew, fNew;
gNew = cellDetails[i][j].g + 1.0;
hNew = calculateHValue(neighbour,
dest);
fNew = gNew + hNew;
// If it isn’t on the open list, add
// it to the open list. Make the
// current square the parent of this
// square. Record the f, g, and h
// costs of the square cell
// OR
// If it is on the open list
// already, check to see if this
// path to that square is better,
// using 'f' cost as the measure.
if (cellDetails[neighbour.first]
[neighbour.second]
.f
== -1
|| cellDetails[neighbour.first]
[neighbour.second]
.f
> fNew) {
openList.emplace(
fNew, neighbour.first,
neighbour.second);
// Update the details of this
// cell
cellDetails[neighbour.first]
[neighbour.second]
.g
= gNew;
cellDetails[neighbour.first]
[neighbour.second]
.h
= hNew;
cellDetails[neighbour.first]
[neighbour.second]
.f
= fNew;
cellDetails[neighbour.first]
[neighbour.second]
.parent
= { i, j };
}
}
}
}
}
}
// When the destination cell is not found and the open
// list is empty, then we conclude that we failed to
// reach the destination cell. This may happen when the
// there is no way to destination cell (due to
// blockages)
printf("Failed to find the Destination Cell\n");
}
// Driver program to test above function
int main()
{
/* Description of the Grid-
1--> The cell is not blocked
0--> The cell is blocked */
array<array<int, 10>, 9> grid{
{ { { 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 } },
{ { 1, 1, 1, 0, 1, 1, 1, 0, 1, 1 } },
{ { 1, 1, 1, 0, 1, 1, 0, 1, 0, 1 } },
{ { 0, 0, 1, 0, 1, 0, 0, 0, 0, 1 } },
{ { 1, 1, 1, 0, 1, 1, 1, 0, 1, 0 } },
{ { 1, 0, 1, 1, 1, 1, 0, 1, 0, 0 } },
{ { 1, 0, 0, 0, 0, 1, 0, 0, 0, 1 } },
{ { 1, 0, 1, 1, 1, 1, 0, 1, 1, 1 } },
{ { 1, 1, 1, 0, 0, 0, 1, 0, 0, 1 } } }
};
// Source is the left-most bottom-most corner
Pair src(8, 0);
// Destination is the left-most top-most corner
Pair dest(0, 0);
aStarSearch(grid, src, dest);
return 0;
}
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA