El algoritmo de búsqueda de ciclos de Floyd o algoritmo Hare-Tortoise es un algoritmo de puntero que utiliza solo dos punteros, moviéndose a través de la secuencia a diferentes velocidades. Este algoritmo se utiliza para encontrar un bucle en una lista enlazada. Utiliza dos punteros, uno que se mueve el doble de rápido que el otro. El más rápido se llama puntero más rápido y el otro se llama puntero lento.
¿Cómo funciona el algoritmo de búsqueda del ciclo de Floyd?
Al recorrer la lista enlazada, ocurrirá una de estas cosas:
- El puntero rápido puede llegar al final (NULL), esto muestra que no hay bucle en la lista enlazada.
- El puntero rápido vuelve a atrapar al puntero lento en algún momento, por lo que existe un bucle en la lista enlazada.
Ejemplo:


Pseudocódigo:
- Inicialice dos punteros y comience a recorrer la lista enlazada.
- Mueva el puntero lento una posición.
- Mueva el puntero rápido dos posiciones.
- Si ambos punteros se encuentran en algún punto, existe un bucle y si el puntero rápido se encuentra con la posición final, entonces no existe ningún bucle.
A continuación se muestra el programa C++ para implementar el enfoque anterior:
C++
// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
// initialize a new head for the linked list
Node* head = NULL;
class Linkedlist {
public:
// insert new value at the start
void insert(int value)
{
Node* newNode = new Node(value);
if (head == NULL)
head = newNode;
else {
newNode->next = head;
head = newNode;
}
}
// detect if there is a loop
// in the linked list
bool detectLoop()
{
Node *slowPointer = head,
*fastPointer = head;
while (slowPointer != NULL
&& fastPointer != NULL
&& fastPointer->next != NULL) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next->next;
if (slowPointer == fastPointer)
return 1;
}
return 0;
}
};
int main()
{
Linkedlist l1;
// inserting new values
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
// adding a loop for the sake
// of this example
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
temp->next = head;
// loop added;
if (l1.detectLoop())
cout << "Loop exists in the"
<< " Linked List" << endl;
else
cout << "Loop does not exists "
<< "in the Linked List" << endl;
return 0;
}
Java
// Java program to implement
// the above approach
import java.util.*;
class GFG{
static class Node {
int data;
Node next;
Node(int data)
{
this.data = data;
next = null;
}
};
// initialize a new head for the linked list
static Node head = null;
static class Linkedlist {
// insert new value at the start
void insert(int value)
{
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
// detect if there is a loop
// in the linked list
boolean detectLoop()
{
Node slowPointer = head,
fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return true;
}
return false;
}
}
public static void main(String[] args)
{
Linkedlist l1 = new Linkedlist();
// inserting new values
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
// adding a loop for the sake
// of this example
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
// loop added;
if (l1.detectLoop())
System.out.print("Loop exists in the"
+ " Linked List" +"\n");
else
System.out.print("Loop does not exists "
+ "in the Linked List" +"\n");
}
}
// This code is contributed by 29AjayKumar
Python3
# Python code for the above approach
class Node:
def __init__(self, d):
self.data = d
self.next = None
# initialize a new head for the linked list
head = None
# detect if there is a loop
# in the linked list
def detectLoop(head):
slowPointer = head
fastPointer = head
while (slowPointer != None
and fastPointer != None
and fastPointer.next != None):
slowPointer = slowPointer.next
fastPointer = fastPointer.next.next
if (slowPointer == fastPointer):
return 1
return 0
# inserting new values
head = Node(10)
head.next = Node(20)
head.next.next = Node(30)
head.next.next.next = Node(40)
head.next.next.next.next = Node(50)
# adding a loop for the sake
# of this example
temp = head
while (temp.next != None):
temp = temp.next
temp.next = head
# loop added;
if (detectLoop(head)):
print("Loop exists in the Linked List")
else:
print("Loop does not exists in the Linked List")
# This code is contributed by Saurabh Jaiswal
C#
// C# program to implement
// the above approach
using System;
using System.Collections.Generic;
public class GFG {
public class Node {
public int data;
public Node next;
public Node(int data) {
this.data = data;
next = null;
}
};
// initialize a new head for the linked list
static Node head = null;
public class Linkedlist
{
// insert new value at the start
public void insert(int value) {
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
// detect if there is a loop
// in the linked list
public bool detectLoop() {
Node slowPointer = head, fastPointer = head;
while (slowPointer != null && fastPointer != null &&
fastPointer.next != null)
{
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return true;
}
return false;
}
}
public static void Main(String[] args) {
Linkedlist l1 = new Linkedlist();
// inserting new values
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
// adding a loop for the sake
// of this example
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
// loop added;
if (l1.detectLoop())
Console.Write("Loop exists in the" + " Linked List" + "\n");
else
Console.Write("Loop does not exists " + "in the Linked List" + "\n");
}
}
// This code is contributed by umadevi9616
Javascript
<script>
// JavaScript code for the above approach
class Node
{
constructor(d)
{
this.data = d;
this.next = null;
}
}
// initialize a new head for the linked list
let head = null;
// detect if there is a loop
// in the linked list
function detectLoop(head) {
let slowPointer = head;
let fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
return 1;
}
return 0;
}
// inserting new values
head = new Node(10);
head.next = new Node(20);
head.next.next = new Node(30);
head.next.next.next = new Node(40);
head.next.next.next.next = new Node(50);
// adding a loop for the sake
// of this example
let temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
// loop added;
if (detectLoop(head))
document.write("Loop exists in the Linked List" + "<br>");
else
document.write("Loop does not exists in the Linked List" + "<br>");
// This code is contributed by Potta Lokesh
</script>
Loop exists in the Linked List
Complejidad temporal: O(n), ya que el bucle se recorre una vez.
Espacio Auxiliar: O(1), solo se utilizan dos punteros por lo tanto complejidad espacial constante.
¿Por qué funciona el algoritmo de Floyd?
Consideremos un ejemplo:
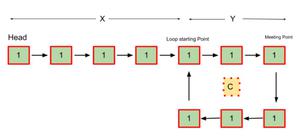
- Dejar,
X = Distancia entre la cabecera (inicio) y el punto de inicio del bucle.
Y = Distancia entre el punto de inicio del bucle y el primer punto de encuentro de ambos punteros.
C = La distancia del bucle
- Así que antes de que ambos punteros se encuentren-
El puntero lento ha viajado X + Y + s * C distancia, donde s es cualquier número constante positivo.
El puntero rápido ha viajado X + Y + f * C distancia, donde f es cualquier número constante positivo.
- Dado que el puntero rápido se mueve el doble de rápido que el puntero lento, podemos decir que el puntero rápido recorrió el doble de la distancia que recorrió el puntero lento. Por lo tanto-
X + Y + f * C = 2 * (X + Y + s * C)
X + Y = f * C – 2 * s * C
Podemos decir eso,
f * C – 2 * s * C = (algún número entero) * C
= K * C
De este modo,
X + Y = K * C – ( 1 )
X = K * C – Y – ( 2 )
Donde K es una constante positiva.
- Ahora, si restablece el puntero lento a la cabeza (posición inicial) y mueve tanto el puntero rápido como el lento una unidad a la vez, se puede observar en la primera y segunda ecuación que ambos se encontrarán después de recorrer X distancia al comienzo de la bucle porque después de restablecer el puntero lento y moverlo X distancia, al mismo tiempo desde el punto de encuentro del bucle, el puntero rápido también viajará K * C – Y distancia (porque ya ha recorrido Y distancia).
- De la ecuación (2) se puede decir que X = K * C – Y, por lo tanto, ambos punteros viajarán la distancia X, es decir, la misma distancia después del Node rosa en algún punto para encontrarse en el punto de inicio del ciclo.
- Aquí, en algún punto, significa que el puntero rápido puede completar la distancia K * C de la cual ya ha cubierto la distancia Y.
A continuación se muestra el programa C++ para implementar el enfoque anterior:
C++
// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
// initialize a new head
// for the linked list
Node* head = NULL;
class Linkedlist {
public:
// insert new value at the start
void insert(int value)
{
Node* newNode = new Node(value);
if (head == NULL)
head = newNode;
else {
newNode->next = head;
head = newNode;
}
}
// detect if there is a loop
// in the linked list
Node* detectLoop()
{
Node *slowPointer = head,
*fastPointer = head;
while (slowPointer != NULL
&& fastPointer != NULL
&& fastPointer->next != NULL) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next->next;
if (slowPointer == fastPointer)
break;
}
// if no loop exists
if (slowPointer != fastPointer)
return NULL;
// reset slow pointer to head
// and traverse again
slowPointer = head;
while (slowPointer != fastPointer) {
slowPointer = slowPointer->next;
fastPointer = fastPointer->next;
}
return slowPointer;
}
};
int main()
{
Linkedlist l1;
// inserting new values
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
// adding a loop for the sake
// of this example
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
// loop added;
temp->next = head;
Node* loopStart = l1.detectLoop();
if (loopStart == NULL)
cout << "Loop does not exists" << endl;
else {
cout << "Loop does exists and starts from "
<< loopStart->data << endl;
}
return 0;
}
Java
// Java program to implement
// the above approach
import java.util.*;
public class GFG{
static class Node {
int data;
Node next;
Node(int data)
{
this.data = data;
next = null;
}
}
// initialize a new head for the linked list
static Node head = null;
static class Linkedlist {
// insert new value at the start
void insert(int value)
{
Node newNode = new Node(value);
if (head == null)
head = newNode;
else {
newNode.next = head;
head = newNode;
}
}
// detect if there is a loop
// in the linked list
public Node detectLoop()
{
Node slowPointer = head,
fastPointer = head;
while (slowPointer != null
&& fastPointer != null
&& fastPointer.next != null) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
if (slowPointer == fastPointer)
break;
}
// if no loop exists
if (slowPointer != fastPointer)
return null;
// reset slow pointer to head
// and traverse again
slowPointer = head;
while (slowPointer != fastPointer) {
slowPointer = slowPointer.next;
fastPointer = fastPointer.next;
}
return slowPointer;
}
}
public static void main(String[] args)
{
Linkedlist l1 = new Linkedlist();
// inserting new values
l1.insert(10);
l1.insert(20);
l1.insert(30);
l1.insert(40);
l1.insert(50);
// adding a loop for the sake
// of this example
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = head;
// loop added;
Node loopStart = l1.detectLoop();
if (loopStart == null)
System.out.println("Loop does not exists" );
else {
System.out.println("Loop does exists and starts from "
+ loopStart.data);
}
}
}
// This code is contributed by jana_sayantan.
Loop does exists and starts from 50
Complejidad del tiempo: O(n), ya que hemos atravesado el ciclo una vez y luego viajado X distancia.
Espacio auxiliar: O(1), ya que solo se utilizan punteros, por lo que la complejidad del espacio es constante.
Publicación traducida automáticamente
Artículo escrito por madnoreason y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA