Algoritmo de Dial (Dijkstra optimizado para pesos de rango pequeño)

Posted on by Rudeus Greyrat

El algoritmo de ruta más corta de Dijkstra se ejecuta en tiempo O (Elog V) cuando se implementa con una representación de lista de adyacencia (consulte la implementación de C y las implementaciones de C++ basadas en STL para obtener más detalles).

Entrada: Fuente = 0, peso máximo W = 14
Salida: 
Distancia del vértice desde la fuente
    0 0
    1 4
    2 12
    3 19
    4 21
    5 11
    6 9
    7 8
   8 14

Considere el siguiente gráfico:

 El camino más corto desde la fuente 0

En este artículo , hemos aprendido cómo encontrar la ruta más corta desde un vértice de origen dado a todos los demás vértices utilizando el algoritmo de ruta más corta de Dijkstra con la Complejidad de tiempo de O (E log V) .

¿Podemos optimizar el algoritmo de ruta más corta de Dijkstra para que funcione mejor que O(E log V) si el peso máximo es pequeño (o el rango de pesos de borde es pequeño)? Por ejemplo, en el diagrama anterior, el peso máximo es 14. Muchas veces el rango de pesos en los bordes está en un rango pequeño (es decir, todos los pesos de los bordes se pueden asignar a 0, 1, 2… w donde w es un número pequeño ). En ese caso, el algoritmo de Dijkstra se puede modificar mediante el uso de diferentes estructuras de datos y cubos, lo que se denomina implementación de marcación del algoritmo de Dijkstra. la complejidad del tiempo es O(E + WV) donde W es el peso máximo en cualquier borde del gráfico, por lo que podemos ver que, si W es pequeño, esta implementación se ejecuta mucho más rápido que el algoritmo tradicional. Las siguientes son observaciones importantes.

  • La distancia máxima entre dos Nodes cualesquiera puede estar en w(V – 1) como máximo (w es el peso máximo de borde y podemos tener bordes en V-1 como máximo entre dos vértices).
  • En el algoritmo de Dijkstra, las distancias se finalizan en no decrecientes, es decir, la distancia de los vértices más cercanos (al origen dado) se finaliza antes que los vértices distantes.

Algoritmo A continuación se muestra el algoritmo completo:

  1. Mantiene unos baldes, numerados 0, 1, 2,…,wV.
  2. El cubo k contiene todos los Nodes etiquetados temporalmente con una distancia igual a k.
  3. Los Nodes en cada cubo están representados por una lista de vértices.
  4. Los cubos 0, 1, 2,…wV se comprueban secuencialmente hasta que se encuentra el primer cubo no vacío. Cada Node contenido en el primer cubo no vacío tiene la etiqueta de distancia mínima por definición.
  5. Uno por uno, estos Nodes con etiquetas de distancia mínima se etiquetan permanentemente y se eliminan del cubo durante el proceso de escaneo.
  6. Por lo tanto, las operaciones que involucran vértice incluyen:
    • Comprobar si un balde está vacío
    • Agregar un vértice a un cubo
    • Eliminación de un vértice de un depósito.
  7. La posición de un vértice etiquetado temporalmente en los cubos se actualiza en consecuencia cuando cambia la etiqueta de distancia de un vértice.
  8. El proceso se repite hasta que todos los vértices estén etiquetados de forma permanente (o se finalicen las distancias de todos los vértices).

 Implementación Dado que la distancia máxima puede ser w(V – 1), creamos cubos wV (más para simplificar el código) para la implementación del algoritmo que puede ser grande si w es grande. 

C++

// C++ Program for Dijkstra's dial implementation
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f
  
// This class represents a directed graph using
// adjacency list representation
class Graph
{
    int V; // No. of vertices
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list< pair<int, int> > *adj;
  
public:
    Graph(int V); // Constructor
  
    // function to add an edge to graph
    void addEdge(int u, int v, int w);
  
    // prints shortest path from s
    void shortestPath(int s, int W);
};
  
// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list< pair<int, int> >[V];
}
  
// adds edge between u and v of weight w
void Graph::addEdge(int u, int v, int w)
{
    adj[u].push_back(make_pair(v, w));
    adj[v].push_back(make_pair(u, w));
}
  
// Prints shortest paths from src to all other vertices.
// W is the maximum weight of an edge
void Graph::shortestPath(int src, int W)
{
    /* With each distance, iterator to that vertex in
    its bucket is stored so that vertex can be deleted
    in O(1) at time of updation. So
    dist[i].first = distance of ith vertex from src vertex
    dits[i].second = iterator to vertex i in bucket number */
    vector<pair<int, list<int>::iterator> > dist(V);
  
    // Initialize all distances as infinite (INF)
    for (int i = 0; i < V; i++)
        dist[i].first = INF;
  
    // Create buckets B[].
    // B[i] keep vertex of distance label i
    list<int> B[W * V + 1];
  
    B[0].push_back(src);
    dist[src].first = 0;
  
    //
    int idx = 0;
    while (1)
    {
        // Go sequentially through buckets till one non-empty
        // bucket is found
        while (B[idx].size() == 0 && idx < W*V)
            idx++;
  
        // If all buckets are empty, we are done.
        if (idx == W * V)
            break;
  
        // Take top vertex from bucket and pop it
        int u = B[idx].front();
        B[idx].pop_front();
  
        // Process all adjacents of extracted vertex 'u' and
        // update their distanced if required.
        for (auto i = adj[u].begin(); i != adj[u].end(); ++i)
        {
            int v = (*i).first;
            int weight = (*i).second;
  
            int du = dist[u].first;
            int dv = dist[v].first;
  
            // If there is shorted path to v through u.
            if (dv > du + weight)
            {
                // If dv is not INF then it must be in B[dv]
                // bucket, so erase its entry using iterator
                // in O(1)
                if (dv != INF)
                    B[dv].erase(dist[v].second);
  
                // updating the distance
                dist[v].first = du + weight;
                dv = dist[v].first;
  
                // pushing vertex v into updated distance's bucket
                B[dv].push_front(v);
  
                // storing updated iterator in dist[v].second
                dist[v].second = B[dv].begin();
            }
        }
    }
  
    // Print shortest distances stored in dist[]
    printf("Vertex Distance from Source\n");
    for (int i = 0; i < V; ++i)
        printf("%d     %d\n", i, dist[i].first);
}
  
// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int V = 9;
    Graph g(V);
  
    // making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);
  
    // maximum weighted edge - 14
    g.shortestPath(0, 14);
  
    return 0;
}
  
// This code is contributed by Aditya Kumar (adityakumar129)

C#

// C# Program for Dijkstra's dial implementation
using System;
using System.Collections.Generic;
  
// This class represents a directed graph using
// adjacency list representation
public class Graph 
{
  static readonly int INF = Int32.MaxValue;
  private int V; // No. of vertices
  // In a weighted graph, we need to store vertex
  // and weight pair for every edge
  private List<Tuple<int, int> >[] adj;
  
  public Graph(int v) // Constructor
  {
    this.V = v;
    this.adj = new List<Tuple<int, int> >[ v ];
    for (int i = 0; i < v; i++)
      this.adj[i] = new List<Tuple<int, int> >();
  }
  
  // function to Add an edge to graph
  // Adds edge between u and v of weight w
  public void AddEdge(int u, int v, int w)
  {
    adj[u].Add(Tuple.Create(v, w));
    adj[v].Add(Tuple.Create(u, w));
  }
  
  // Prints shortest paths from src to all other vertices.
  // W is the maximum weight of an edge
  public void shortestPath(int src, int W)
  {
    /* With each distance, iterator to that vertex in
        its bucket is stored so that vertex can be deleted
        in O(1) at time of updation. So
        dist[i].first = distance of ith vertex from src
        vertex dits[i].second = iterator to vertex i in
        bucket number */
    int[] dist = new int[V];
  
    // Initialize all distances as infinite (INF)
    for (int i = 0; i < V; i++)
      dist[i] = INF;
  
    // Create buckets B[].
    // B[i] keep vertex of distance label i
    List<int>[] B = new List<int>[ W * V + 1 ];
    for (int i = 0; i < W * V + 1; i++)
      B[i] = new List<int>();
  
    B[0].Add(src);
    dist[src] = 0;
  
    int idx = 0;
    while (true) {
      // Go sequentially through buckets till one
      // non-empty bucket is found
      while (B[idx].Count == 0 && idx < W * V)
        idx++;
  
      // If all buckets are empty, we are done.
      if (idx == W * V)
        break;
  
      // Take top vertex from bucket and pop it
      int u = B[idx][0];
      B[idx].Remove(u);
  
      // Process all adjacents of extracted vertex 'u'
      // and update their distances if required.
      foreach(Tuple<int, int> i in adj[u])
      {
        int v = i.Item1;
        int weight = i.Item2;
  
        int du = dist[u];
        int dv = dist[v];
  
        // If there is shorted path to v through u.
        if (dv > du + weight) {
          // updating the distance
          dist[v] = du + weight;
          dv = dist[v];
  
          // pushing vertex v into updated
          // distance's bucket
          B[dv].Insert(0, v);
        }
      }
    }
  
    // Print shortest distances stored in dist[]
    Console.WriteLine("Vertex Distance from Source");
    for (int i = 0; i < V; ++i)
      Console.WriteLine("{0}     {1}", i, dist[i]);
  }
}
  
class GFG {
  // Driver program to test methods of graph class
  static void Main(string[] args)
  {
    // create the graph given in above figure
    int V = 9;
    Graph g = new Graph(V);
  
    // making above shown graph
    g.AddEdge(0, 1, 4);
    g.AddEdge(0, 7, 8);
    g.AddEdge(1, 2, 8);
    g.AddEdge(1, 7, 11);
    g.AddEdge(2, 3, 7);
    g.AddEdge(2, 8, 2);
    g.AddEdge(2, 5, 4);
    g.AddEdge(3, 4, 9);
    g.AddEdge(3, 5, 14);
    g.AddEdge(4, 5, 10);
    g.AddEdge(5, 6, 2);
    g.AddEdge(6, 7, 1);
    g.AddEdge(6, 8, 6);
    g.AddEdge(7, 8, 7);
  
    // maximum weighted edge - 14
    g.shortestPath(0, 14);
  }
}
  
// This code is contributed by cavi4762

Producción:

Vertex Distance from Source
0     0
1     4
2     12
3     19
4     21
5     11
6     9
7     8
8     14

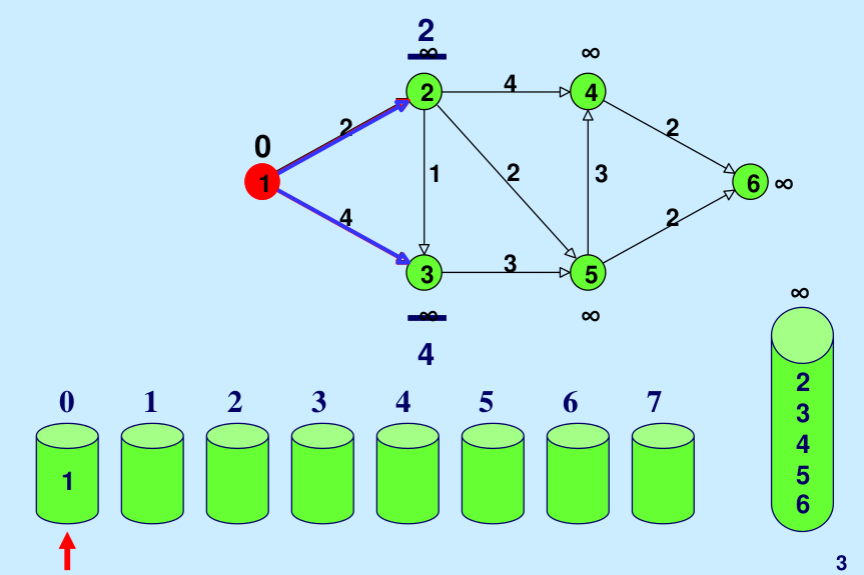
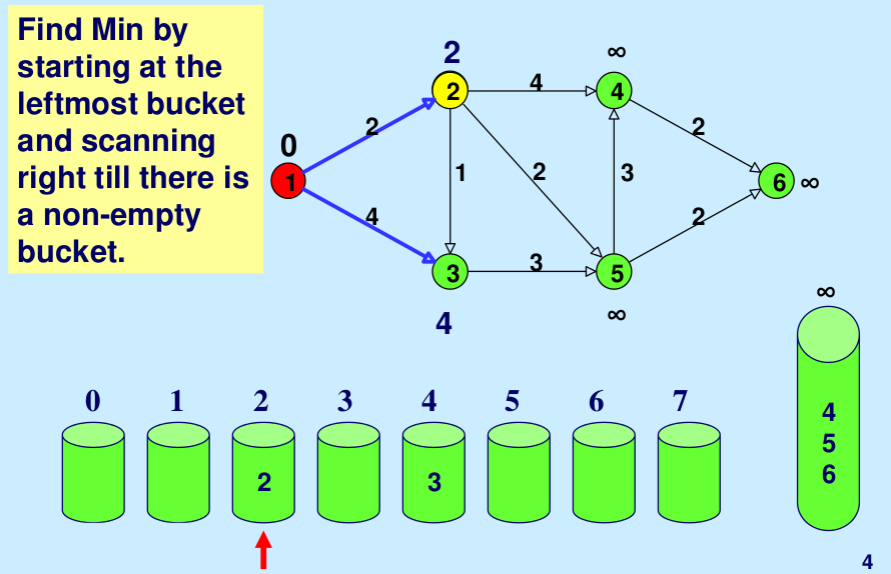
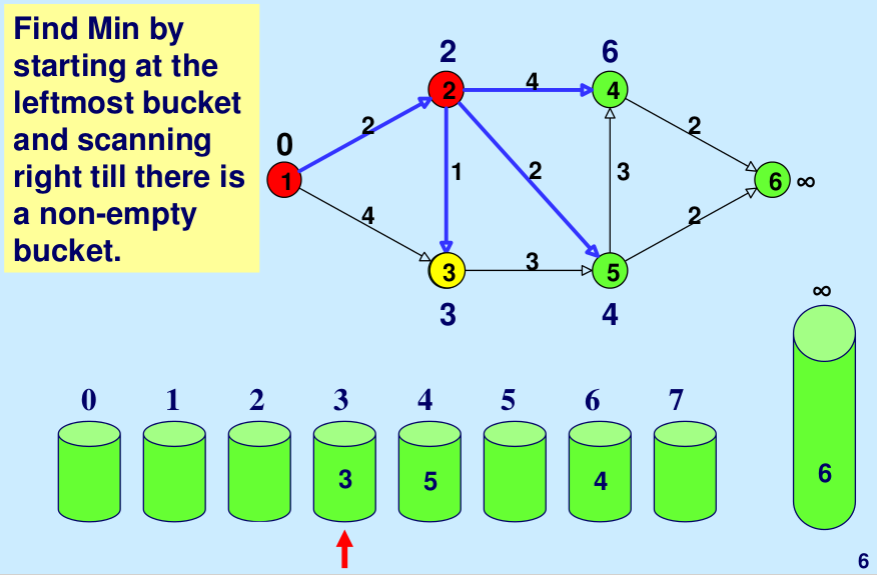
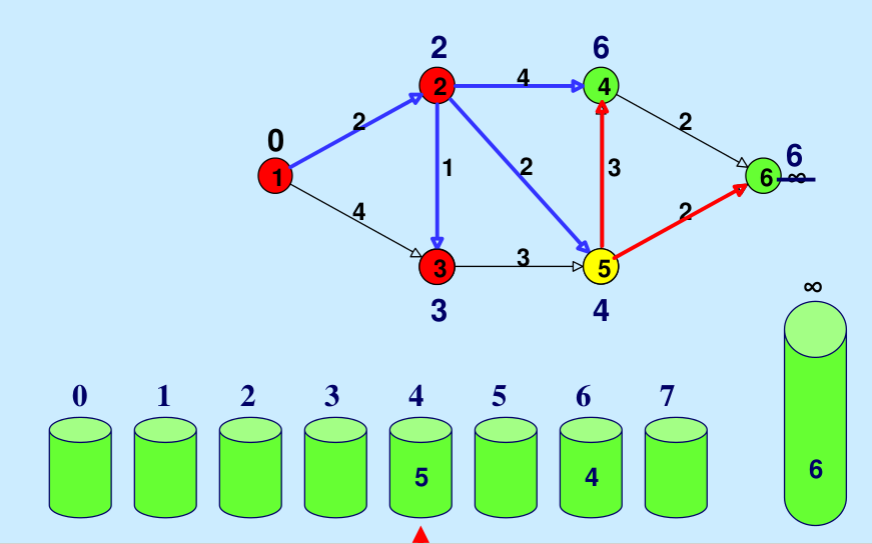
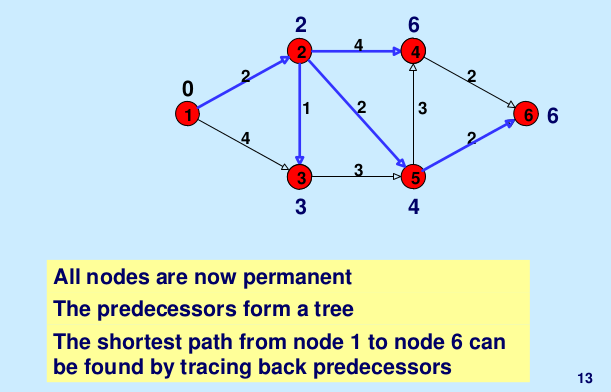
 Ilustración: A continuación se muestra la ilustración paso a paso tomada de aquí .step1 step2 step3 step4 step5 step6 step7 step8 step10 step11 step12 step13  

Este artículo es una contribución de Utkarsh Trivedi. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *