En análisis numérico y álgebra lineal, la descomposición LU (donde ‘LU’ significa ‘inferior superior’ y también llamada factorización LU) factoriza una array como el producto de una array triangular inferior y una array triangular superior. Las computadoras generalmente resuelven sistemas cuadrados de ecuaciones lineales usando la descomposición LU, y también es un paso clave cuando se invierte una array o se calcula el determinante de una array. La descomposición LU fue introducida por el matemático Tadeusz Banachiewicz en 1938.
Sea A una array cuadrada. Una factorización LU se refiere a la factorización de A, con ordenaciones o permutaciones de fila y/o columna adecuadas, en dos factores, una array triangular inferior L y una array triangular superior U, A=LU .
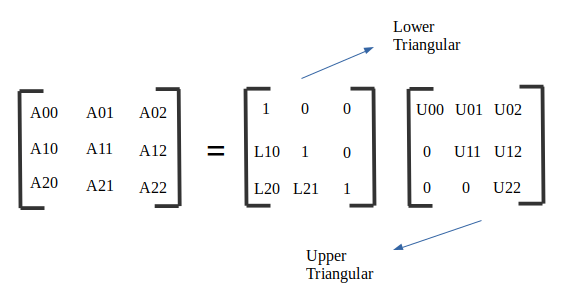
Algoritmo de Doolittle:
Siempre es posible factorizar una array cuadrada en una array triangular inferior y una array triangular superior. Es decir, [A] = [L][U]
El método de Doolittle proporciona una forma alternativa de factorizar A en una descomposición LU sin pasar por la molestia de la eliminación gaussiana .
Para una array A general de n×n, asumimos que existe una descomposición LU y escribimos la forma de L y U explícitamente. Luego resolvemos sistemáticamente las entradas en L y U a partir de las ecuaciones que resultan de las multiplicaciones necesarias para A=LU.
Los términos de la array U están dados por:
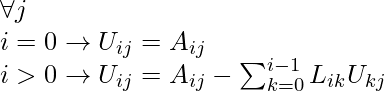
Y los términos para la array L:
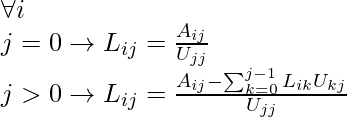
Ejemplo :
Input :

Output :

Implementación:
C++
// C++ Program to decompose a matrix into
// lower and upper triangular matrix
#include <bits/stdc++.h>
using namespace std;
const int MAX = 100;
void luDecomposition(int mat[][MAX], int n)
{
int lower[n][n], upper[n][n];
memset(lower, 0, sizeof(lower));
memset(upper, 0, sizeof(upper));
// Decomposing matrix into Upper and Lower
// triangular matrix
for (int i = 0; i < n; i++)
{
// Upper Triangular
for (int k = i; k < n; k++)
{
// Summation of L(i, j) * U(j, k)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[i][j] * upper[j][k]);
// Evaluating U(i, k)
upper[i][k] = mat[i][k] - sum;
}
// Lower Triangular
for (int k = i; k < n; k++)
{
if (i == k)
lower[i][i] = 1; // Diagonal as 1
else
{
// Summation of L(k, j) * U(j, i)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[k][j] * upper[j][i]);
// Evaluating L(k, i)
lower[k][i]
= (mat[k][i] - sum) / upper[i][i];
}
}
}
// setw is for displaying nicely
cout << setw(6)
<< " Lower Triangular"
<< setw(32)
<< "Upper Triangular" << endl;
// Displaying the result :
for (int i = 0; i < n; i++)
{
// Lower
for (int j = 0; j < n; j++)
cout << setw(6) << lower[i][j] << "\t";
cout << "\t";
// Upper
for (int j = 0; j < n; j++)
cout << setw(6) << upper[i][j] << "\t";
cout << endl;
}
}
// Driver code
int main()
{
int mat[][MAX]
= { { 2, -1, -2 }, { -4, 6, 3 }, { -4, -2, 8 } };
luDecomposition(mat, 3);
return 0;
}
Java
// Java Program to decompose a matrix into
// lower and upper triangular matrix
class GFG {
static int MAX = 100;
static String s = "";
static void luDecomposition(int[][] mat, int n)
{
int[][] lower = new int[n][n];
int[][] upper = new int[n][n];
// Decomposing matrix into Upper and Lower
// triangular matrix
for (int i = 0; i < n; i++)
{
// Upper Triangular
for (int k = i; k < n; k++)
{
// Summation of L(i, j) * U(j, k)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[i][j] * upper[j][k]);
// Evaluating U(i, k)
upper[i][k] = mat[i][k] - sum;
}
// Lower Triangular
for (int k = i; k < n; k++)
{
if (i == k)
lower[i][i] = 1; // Diagonal as 1
else
{
// Summation of L(k, j) * U(j, i)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[k][j] * upper[j][i]);
// Evaluating L(k, i)
lower[k][i]
= (mat[k][i] - sum) / upper[i][i];
}
}
}
// setw is for displaying nicely
System.out.println(setw(2) + " Lower Triangular"
+ setw(10) + "Upper Triangular");
// Displaying the result :
for (int i = 0; i < n; i++)
{
// Lower
for (int j = 0; j < n; j++)
System.out.print(setw(4) + lower[i][j]
+ "\t");
System.out.print("\t");
// Upper
for (int j = 0; j < n; j++)
System.out.print(setw(4) + upper[i][j]
+ "\t");
System.out.print("\n");
}
}
static String setw(int noOfSpace)
{
s = "";
for (int i = 0; i < noOfSpace; i++)
s += " ";
return s;
}
// Driver code
public static void main(String arr[])
{
int mat[][] = { { 2, -1, -2 },
{ -4, 6, 3 },
{ -4, -2, 8 } };
luDecomposition(mat, 3);
}
}
/* This code contributed by PrinciRaj1992 */
Python3
# Python3 Program to decompose
# a matrix into lower and
# upper triangular matrix
MAX = 100
def luDecomposition(mat, n):
lower = [[0 for x in range(n)]
for y in range(n)]
upper = [[0 for x in range(n)]
for y in range(n)]
# Decomposing matrix into Upper
# and Lower triangular matrix
for i in range(n):
# Upper Triangular
for k in range(i, n):
# Summation of L(i, j) * U(j, k)
sum = 0
for j in range(i):
sum += (lower[i][j] * upper[j][k])
# Evaluating U(i, k)
upper[i][k] = mat[i][k] - sum
# Lower Triangular
for k in range(i, n):
if (i == k):
lower[i][i] = 1 # Diagonal as 1
else:
# Summation of L(k, j) * U(j, i)
sum = 0
for j in range(i):
sum += (lower[k][j] * upper[j][i])
# Evaluating L(k, i)
lower[k][i] = int((mat[k][i] - sum) /
upper[i][i])
# setw is for displaying nicely
print("Lower Triangular\t\tUpper Triangular")
# Displaying the result :
for i in range(n):
# Lower
for j in range(n):
print(lower[i][j], end="\t")
print("", end="\t")
# Upper
for j in range(n):
print(upper[i][j], end="\t")
print("")
# Driver code
mat = [[2, -1, -2],
[-4, 6, 3],
[-4, -2, 8]]
luDecomposition(mat, 3)
# This code is contributed by mits
C#
// C# Program to decompose a matrix into
// lower and upper triangular matrix
using System;
class GFG {
static int MAX = 100;
static String s = "";
static void luDecomposition(int[, ] mat, int n)
{
int[, ] lower = new int[n, n];
int[, ] upper = new int[n, n];
// Decomposing matrix into Upper and Lower
// triangular matrix
for (int i = 0; i < n; i++)
{
// Upper Triangular
for (int k = i; k < n; k++)
{
// Summation of L(i, j) * U(j, k)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[i, j] * upper[j, k]);
// Evaluating U(i, k)
upper[i, k] = mat[i, k] - sum;
}
// Lower Triangular
for (int k = i; k < n; k++)
{
if (i == k)
lower[i, i] = 1; // Diagonal as 1
else
{
// Summation of L(k, j) * U(j, i)
int sum = 0;
for (int j = 0; j < i; j++)
sum += (lower[k, j] * upper[j, i]);
// Evaluating L(k, i)
lower[k, i]
= (mat[k, i] - sum) / upper[i, i];
}
}
}
// setw is for displaying nicely
Console.WriteLine(setw(2) + " Lower Triangular"
+ setw(10) + "Upper Triangular");
// Displaying the result :
for (int i = 0; i < n; i++)
{
// Lower
for (int j = 0; j < n; j++)
Console.Write(setw(4) + lower[i, j] + "\t");
Console.Write("\t");
// Upper
for (int j = 0; j < n; j++)
Console.Write(setw(4) + upper[i, j] + "\t");
Console.Write("\n");
}
}
static String setw(int noOfSpace)
{
s = "";
for (int i = 0; i < noOfSpace; i++)
s += " ";
return s;
}
// Driver code
public static void Main(String[] arr)
{
int[, ] mat = { { 2, -1, -2 },
{ -4, 6, 3 },
{ -4, -2, 8 } };
luDecomposition(mat, 3);
}
}
// This code is contributed by Princi Singh
PHP
<?php
// PHP Program to decompose
// a matrix into lower and
// upper triangular matrix
$MAX = 100;
function luDecomposition($mat, $n)
{
$lower;
$upper;
for($i = 0; $i < $n; $i++)
for($j = 0; $j < $n; $j++)
{
$lower[$i][$j]= 0;
$upper[$i][$j]= 0;
}
// Decomposing matrix
// into Upper and Lower
// triangular matrix
for ($i = 0; $i < $n; $i++)
{
// Upper Triangular
for ($k = $i; $k < $n; $k++)
{
// Summation of
// L(i, j) * U(j, k)
$sum = 0;
for ($j = 0; $j < $i; $j++)
$sum += ($lower[$i][$j] *
$upper[$j][$k]);
// Evaluating U(i, k)
$upper[$i][$k] = $mat[$i][$k] - $sum;
}
// Lower Triangular
for ($k = $i; $k < $n; $k++)
{
if ($i == $k)
$lower[$i][$i] = 1; // Diagonal as 1
else
{
// Summation of L(k, j) * U(j, i)
$sum = 0;
for ($j = 0; $j < $i; $j++)
$sum += ($lower[$k][$j] *
$upper[$j][$i]);
// Evaluating L(k, i)
$lower[$k][$i] = (int)(($mat[$k][$i] -
$sum) / $upper[$i][$i]);
}
}
}
// setw is for
// displaying nicely
echo "\t\tLower Triangular";
echo "\t\t\tUpper Triangular\n";
// Displaying the result :
for ($i = 0; $i < $n; $i++)
{
// Lower
for ($j = 0; $j < $n; $j++)
echo "\t" . $lower[$i][$j] . "\t";
echo "\t";
// Upper
for ($j = 0; $j < $n; $j++)
echo $upper[$i][$j] . "\t";
echo "\n";
}
}
// Driver code
$mat = array(array(2, -1, -2),
array(-4, 6, 3),
array(-4, -2, 8));
luDecomposition($mat, 3);
// This code is contributed by mits
?>
Javascript
<script>
// Javascript Program to decompose a matrix
// into lower and upper triangular matrix
// function MAX = 100;
var s = "";
function luDecomposition(mat, n)
{
var lower = Array(n).fill(0).map(
x => Array(n).fill(0));
var upper = Array(n).fill(0).map(
x => Array(n).fill(0));
// Decomposing matrix into Upper and
// Lower triangular matrix
for(var i = 0; i < n; i++)
{
// Upper Triangular
for(var k = i; k < n; k++)
{
// Summation of L(i, j) * U(j, k)
var sum = 0;
for(var j = 0; j < i; j++)
sum += (lower[i][j] * upper[j][k]);
// Evaluating U(i, k)
upper[i][k] = mat[i][k] - sum;
}
// Lower Triangular
for(var k = i; k < n; k++)
{
if (i == k)
// Diagonal as 1
lower[i][i] = 1;
else
{
// Summation of L(k, j) * U(j, i)
var sum = 0;
for(var j = 0; j < i; j++)
sum += (lower[k][j] * upper[j][i]);
// Evaluating L(k, i)
lower[k][i] = parseInt((mat[k][i] - sum) /
upper[i][i]);
}
}
}
// Setw is for displaying nicely
document.write(setw(2) + "Lower Triangular" +
setw(10) + "Upper Triangular<br>");
// Displaying the result :
for(var i = 0; i < n; i++)
{
// Lower
for(var j = 0; j < n; j++)
document.write(setw(4) +
lower[i][j] + "\t");
document.write(setw(10));
// Upper
for(var j = 0; j < n; j++)
document.write(setw(4) +
upper[i][j] + "\t");
document.write("<br>");
}
}
function setw(noOfSpace)
{
var s = "";
for(i = 0; i < noOfSpace; i++)
s += " ";
return s;
}
// Driver code
var mat = [ [ 2, -1, -2 ],
[ -4, 6, 3 ],
[ -4, -2, 8 ] ];
luDecomposition(mat, 3);
// This code is contributed by Amit Katiyar
</script>
Lower Triangular Upper Triangular
1 0 0 2 -1 -2
-2 1 0 0 4 -1
-2 -1 1 0 0 3
Este artículo es una contribución de Shubham Rana . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA