Dada la coordenada de dos puntos A(x1, y1) y B(x2, y2) tales que x1 < x2 e y1 < y2. La tarea de encontrar todos los puntos intermedios necesarios para dibujar la línea AB en la pantalla de la computadora de píxeles. Tenga en cuenta que cada píxel tiene coordenadas enteras.
Hemos discutido a continuación los algoritmos para esta tarea.
En esta publicación, se analiza el algoritmo de dibujo de línea de punto medio, que es una forma diferente de representar el algoritmo de Bresenham presentado en la publicación anterior.
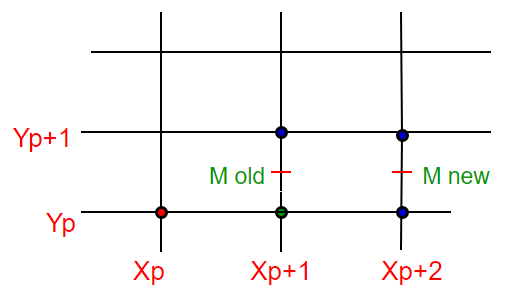
Como se discutió en la publicación anterior , para cualquier píxel anterior dado/calculado P (X p , Y p ), hay dos candidatos para el siguiente píxel más cercano a la línea, E (X p +1, Y p ) y NE (X p +1, Y p +1) ( E significa Este y NE significa Noreste).
En el algoritmo de punto medio hacemos lo siguiente.
- Encuentra el medio de dos posibles puntos siguientes. El medio de E(X p +1, Y p ) y NE(X p +1, Y p +1) es M(X p+1 , Y p +1/2).
- Si M está por encima de la línea, elija E como el siguiente punto.
- Si M está debajo de la línea, elija NE como el siguiente punto.

¿Cómo encontrar si un punto está encima de una línea o debajo de una línea?
A continuación se presentan algunas suposiciones para mantener el algoritmo simple.
- Dibujamos una línea de izquierda a derecha.
- x1 < x2 y y1 < y2
- La pendiente de la línea está entre 0 y 1. Dibujamos una línea de abajo a la izquierda a arriba a la derecha.
Los casos que no sean los supuestos anteriores se pueden manejar mediante la reflexión.
Let us consider a line y = mx + B.
We can re-write the equation as :
y = (dy/dx)x + B or
(dy)x + B(dx) - y(dx) = 0
Let F(x, y) = (dy)x - y(dx) + B(dx) -----(1)
Let we are given two end points of a line (under
above assumptions)
-> For all points (x,y) on the line,
the solution to F(x, y) is 0.
-> For all points (x,y) above the line,
F(x, y) result in a negative number.
-> And for all points (x,y) below the line,
F(x, y) result in a positive number.
Esta relación se usa para determinar la
posición relativa de M
M = (X p+1 , Y p+1 /2)
Entonces nuestro parámetro de decisión d es,
d = F(M) = F(X p+1 , Y p+ 1/2 )
¿Cómo encontrar eficientemente el nuevo valor de d a partir de su valor anterior?
Para simplificar, escribamos F(x, y) como ax + by + c.
Donde a = dy
b = -dx
c = B*dx
Obtuvimos estos valores de la ecuación anterior (1)
Caso 1: Si se elige E, entonces para el siguiente punto:
dnew = F(X p +2, Y p+1 /2 )
= a(X p +2) + b(Y p+1 /2) + c
dold = a(X p +1) + b(Y p+1 /2) + c
Diferencia (O delta) de dos distancias:
DELd = dnew – dold
= a(X p +2)- a(X p +1 )+ b(Y p+1 /2)- b(Y p+1 /2)+ cc
= a(X p ) +2a – a(X p ) – a
= a.
Por lo tanto, dnuevo = dold + dy. (como a = dy)
Caso 2: si se elige NE, entonces para el siguiente punto:
dnuevo = F(X p +2, Y p +3/2)
= a(X p +2) + b(Y p +3/2) + c
dold = a(X p +1) + b(Y p +1/2) + c
Diferencia (O delta) de dos distancias:
DELd = dnew -dold
= a(X p +2)- a(X p +1)+ b(Y p +3/2)- b(Y p +1/2)+ cc
= a(X p ) + 2a – a(X p ) – a + b(Y p ) + 3/2b – b( Y p ) -1/2b
= a + b
Por lo tanto, dnuevo = dold + dy – dx. (como a = dy , b = -dx)
Cálculo Para el valor inicial del parámetro de decisión d0:
d0 = F(X1+1 , Y1+1/2)
= a(X1 + 1) + b(Y1 + 1/2) +c
= aX1+ bY1 + c + a + b /2
= F(X1,Y1) + a + b/2
= a + b/2 (como F(X1, Y1) = 0 )
d0 = dy – dx/2. (como a = dy, b = -dx)
Algoritmo:
Input (X1,Y1) and (X2,Y2)
dy = Y2- Y1
dx = X2 - X1
// initial value of
// decision parameter d
if(dy<=dx){
d = dy - (dx/2)
x = X1 , y = Y1
// plot initial given point
Plot(x , y)
// iterate through value of X
while(x < X2)
x = x+1
// 'E' is chosen
if (d < 0)
d = d + dy
// 'NE' is chosen
else
d = d + dy - dx
y = y+1
Plot(x,y)}
else if(dx<=dy)
{
d = dx - (dy/2)
x = X1 , y = Y1
// plot initial given point
Plot(x , y)
// iterate through value of X
while(y< Y2)
y= y+1
// 'E' is chosen
if (d < 0)
d = d + dx
// 'NE' is chosen
else
d = d + dx - dy
x= x+1
Plot(x,y)
}
A continuación se muestra la implementación de la idea anterior:
C++
// C++ program for Mid-point line generation
#include<bits/stdc++.h>
using namespace std;
// Header file for including graphics functions
// #include<graphics.h>
// midPoint function for line generation
void midPoint(int X1, int Y1, int X2, int Y2)
{
// calculate dx & dy
int dx = X2 - X1;
int dy = Y2 - Y1;
if(dy<=dx){
// initial value of decision parameter d
int d = dy - (dx/2);
int x = X1, y = Y1;
// Plot initial given point
// putpixel(x,y) can be used to print pixel
// of line in graphics
cout << x << "," << y << "\n";
// iterate through value of X
while (x < X2)
{
x++;
// E or East is chosen
if (d < 0)
d = d + dy;
// NE or North East is chosen
else
{
d += (dy - dx);
y++;
}
// Plot intermediate points
// putpixel(x,y) is used to print pixel
// of line in graphics
cout << x << "," << y << "\n";
}
}
else if(dx<dy)
{
// initial value of decision parameter d
int d = dx - (dy/2);
int x = X1, y = Y1;
// Plot initial given point
// putpixel(x,y) can be used to print pixel
// of line in graphics
cout << x << "," << y << "\n";
// iterate through value of X
while (y < Y2)
{
y++;
// E or East is chosen
if (d < 0)
d = d + dx;
// NE or North East is chosen
// NE or North East is chosen
else
{
d += (dx - dy);
x++;
}
// Plot intermediate points
// putpixel(x,y) is used to print pixel
// of line in graphics
cout << x << "," << y << "\n";
}
}
}
// Driver program
int main()
{
// graphics driver and mode
// used in graphics.h
// int gd = DETECT, gm;
// Initialize graphics function
// initgraph (&gd, &gm, "");
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
return 0;
}
Java
// Java program for Mid-point
// line generation
class GFG
{
// midPoint function for line generation
static void midPoint(int X1, int Y1,
int X2, int Y2)
{
// calculate dx & dy
int dx = X2 - X1;
int dy = Y2 - Y1;
// initial value of decision
// parameter d
int d = dy - (dx/2);
int x = X1, y = Y1;
// Plot initial given point
// putpixel(x,y) can be used to
// print pixel of line in graphics
System.out.print(x +"," + y + "\n");
// iterate through value of X
while (x < X2)
{
x++;
// E or East is chosen
if (d < 0)
d = d + dy;
// NE or North East is chosen
else
{
d += (dy - dx);
y++;
}
// Plot intermediate points
// putpixel(x,y) is used to print
// pixel of line in graphics
System.out.print(x +"," + y + "\n");
}
}
// Driver code
public static void main (String[] args)
{
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
}
}
// This code is contributed by Anant Agarwal.
Python 3
# Python3 program for Mid-point # line generation # midPoint function for line generation def midPoint(X1,Y1,X2,Y2): # calculate dx & dy dx = X2 - X1 dy = Y2 - Y1 # initial value of decision parameter d d = dy - (dx/2) x = X1 y = Y1 # Plot initial given point # putpixel(x,y) can be used to print pixel # of line in graphics print(x,",",y,"\n") # iterate through value of X while (x < X2): x=x+1 # E or East is chosen if(d < 0): d = d + dy # NE or North East is chosen else: d = d + (dy - dx) y=y+1 # Plot intermediate points # putpixel(x,y) is used to print pixel # of line in graphics print(x,",",y,"\n") # Driver program if __name__=='__main__': X1 = 2 Y1 = 2 X2 = 8 Y2 = 5 midPoint(X1, Y1, X2, Y2) # This code is contributed by ash264
C#
// C# program for Mid-point
// line generation
using System;
class GFG {
// midPoint function for line
// generation
static void midPoint(int X1, int Y1,
int X2, int Y2)
{
// calculate dx & dy
int dx = X2 - X1;
int dy = Y2 - Y1;
// initial value of decision
// parameter d
int d = dy - (dx/2);
int x = X1, y = Y1;
// Plot initial given point
// putpixel(x,y) can be used
// to print pixel of line in
// graphics
Console.Write(x + "," + y + "\n");
// iterate through value of X
while (x < X2)
{
x++;
// E or East is chosen
if (d < 0)
d = d + dy;
// NE or North East is chosen
else
{
d += (dy - dx);
y++;
}
// Plot intermediate points
// putpixel(x,y) is used to print
// pixel of line in graphics
Console.Write(x + "," + y + "\n");
}
}
// Driver code
public static void Main ()
{
int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
}
}
// This code is contributed by nitin mittal.
PHP
<?php
// PHP program for Mid-point
// line generation
// midPoint function for
// line generation
function midPoint($X1, $Y1,
$X2, $Y2)
{
// calculate dx & dy
$dx = $X2 - $X1;
$dy = $Y2 - $Y1;
// initial value of
// decision parameter d
$d = $dy - ($dx/2);
$x = $X1;
$y = $Y1;
// Plot initial given point
// putpixel(x,y) can be used
// to print pixel of line
// in graphics
echo $x , "," , $y , "\n";
// iterate through
// value of X
while ($x < $X2)
{
$x++;
// E or East is chosen
if ($d < 0)
$d = $d + $dy;
// NE or North East
// is chosen
else
{
$d += ($dy - $dx);
$y++;
}
// Plot intermediate points
// putpixel(x,y) is used
// to print pixel of
// line in graphics
echo $x , "," ,$y , "\n";
}
}
// Driver Code
$X1 = 2;
$Y1 = 2;
$X2 = 8;
$Y2 = 5;
midPoint($X1, $Y1, $X2, $Y2);
// This code is contributed by nitin mittal.
?>
Javascript
<script>
// JavaScript program for the above approach
// midPoint function for line generation
function midPoint(X1, Y1, X2, Y2)
{
// calculate dx & dy
let dx = X2 - X1;
let dy = Y2 - Y1;
// initial value of decision
// parameter d
let d = dy - (dx/2);
let x = X1, y = Y1;
// Plot initial given point
// putpixel(x,y) can be used to
// print pixel of line in graphics
document.write(x +"," + y + "<br/>");
// iterate through value of X
while (x < X2)
{
x++;
// E or East is chosen
if (d < 0)
d = d + dy;
// NE or North East is chosen
else
{
d += (dy - dx);
y++;
}
// Plot intermediate points
// putpixel(x,y) is used to print
// pixel of line in graphics
document.write(x + "," + y + "<br/>");
}
}
// Driver Code
let X1 = 2, Y1 = 2, X2 = 8, Y2 = 5;
midPoint(X1, Y1, X2, Y2);
// This code is contributed by chinmoy1997pal.
</script>
Producción:
2,2 3,3 4,3 5,4 6,4 7,5 8,5
Complejidad de tiempo: O(x2 – x1)
Espacio auxiliar: O(1)
Referencias:
http://www.eng.utah.edu/~cs5600/slides/Wk%202%20Lec02_Bresenham.pdf
Este artículo es una contribución de Shivam Pradhan ( anuj_charm) . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA