Algoritmo de Johnson para caminos más cortos de todos los pares

El problema es encontrar los caminos más cortos entre cada par de vértices en un gráfico dirigido ponderado dado y los pesos pueden ser negativos. Hemos discutido el algoritmo de Floyd Warshall para este problema. La complejidad temporal del algoritmo de Floyd Warshall es Θ(V ³ ). 

Usando el algoritmo de Johnson, podemos encontrar los caminos más cortos de todos los pares en tiempo O(V ² log V + VE). El algoritmo de Johnson usa Dijkstra y Bellman-Ford como subrutinas. Si aplicamos el algoritmo de camino más corto de fuente única de Dijkstra para cada vértice, considerando cada vértice como la fuente, podemos encontrar todos los pares de caminos más cortos en tiempo O(V*VLogV). 

Entonces, usar la ruta más corta de fuente única de Dijkstra parece ser una mejor opción que el Algoritmo de Floyd Warshall ( https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/?ref=lbp ), pero el problema con Dijkstra El algoritmo es que no funciona para el borde de peso negativo. La idea del algoritmo de Johnson es volver a ponderar todos los bordes y hacerlos todos positivos, luego aplicar el algoritmo de Dijkstra para cada vértice. 

¿Cómo transformar un gráfico dado en un gráfico con todos los bordes de peso no negativos? 

Uno puede pensar en un enfoque simple para encontrar el borde de peso mínimo y agregar este peso a todos los bordes. Desafortunadamente, esto no funciona, ya que puede haber una cantidad diferente de bordes en diferentes rutas (consulte esto para ver un ejemplo). Si hay varios caminos desde un vértice u hasta v, entonces todos los caminos deben incrementarse en la misma cantidad, de modo que el camino más corto siga siendo el más corto en el gráfico transformado. La idea del algoritmo de Johnson es asignar un peso a cada vértice. Sea h[u] el peso asignado al vértice u. 

Reponderamos los bordes usando pesos de vértices. Por ejemplo, para una arista (u, v) de peso w(u, v), el nuevo peso se convierte en w(u, v) + h[u] – h[v]. Lo bueno de esta nueva ponderación es que todo el conjunto de caminos entre dos vértices se incrementa en la misma cantidad y todos los pesos negativos se vuelven no negativos. Considere cualquier camino entre dos vértices s y t, el peso de cada camino aumenta en h[s] – h[t], y todos los valores h[] de los vértices en el camino de s a t se cancelan entre sí. 

¿Cómo calculamos los valores de h[]? 

Para ello se utiliza el algoritmo de Bellman-Ford . A continuación se muestra el algoritmo completo. Se agrega un nuevo vértice al gráfico y se conecta a todos los vértices existentes. Los valores de distancia más cortos desde el nuevo vértice a todos los vértices existentes son valores h[]. 

Algoritmo: 

1. Sea G el gráfico dado. Agregue un nuevo vértice s al gráfico, agregue aristas desde el nuevo vértice a todos los vértices de G. Sea G’ el gráfico modificado. 
2. Ejecute el algoritmo Bellman-Ford en G’ con s como fuente. Sean las distancias calculadas por Bellman-Ford h[0], h[1], .. h[V-1]. Si encontramos un ciclo de peso negativo, entonces regresa. Tenga en cuenta que el ciclo de peso negativo no puede ser creado por nuevos vértices ya que no hay borde en s. Todas las aristas son del s. 
3. Vuelva a ponderar los bordes del gráfico original. Para cada borde (u, v), asigne el nuevo peso como “peso original + h[u] – h[v]”. 
4. Elimine los vértices agregados y ejecute el algoritmo de Dijkstra para cada vértice. 

¿Cómo asegura la transformación bordes de peso no negativos? 

La siguiente propiedad siempre se cumple con los valores de h[], ya que son las distancias más cortas.

   h[v] <= h[u] + w(u, v) 

La propiedad simplemente significa que la distancia más corta de s a v debe ser menor o igual que la distancia más corta de s a u más el peso del borde (u, v). Los nuevos pesos son w(u, v) + h[u] – h[v]. El valor de los nuevos pesos debe ser mayor o igual a cero debido a la desigualdad “h[v] <= h[u] + w(u, v)”. 

Ejemplo: Consideremos el siguiente gráfico. 

 Agregamos una fuente s y agregamos bordes desde s a todos los vértices del gráfico original. En el siguiente diagrama s es 4. 

 

 

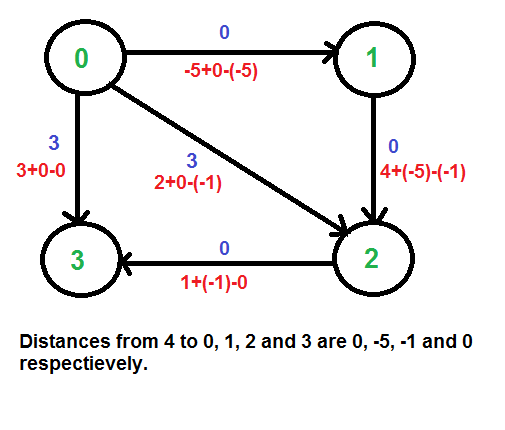
Calculamos las distancias más cortas de 4 a todos los demás vértices usando el algoritmo Bellman-Ford. Las distancias más cortas de 4 a 0, 1, 2 y 3 son 0, -5, -1 y 0 respectivamente, es decir, h[] = {0, -5, -1, 0}. Una vez que obtengamos estas distancias, eliminamos el vértice de origen 4 y volvemos a ponderar los bordes usando la siguiente fórmula. w(u, v) = w(u, v) + h[u] – h[v].

  

Dado que todos los pesos son positivos ahora, podemos ejecutar el algoritmo de ruta más corta de Dijkstra para cada vértice como fuente. 

Complejidad del tiempo: los pasos principales en el algoritmo son el algoritmo Bellman-Ford llamado una vez y Dijkstra llamado V veces. La complejidad temporal de Bellman Ford es O(VE) y la complejidad temporal de Dijkstra es O(VLogV). Entonces, la complejidad del tiempo total es O(V ² log V + VE). 

La complejidad temporal del algoritmo de Johnson se convierte en la misma que la del algoritmo de Floyd Warshall ( https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/?ref=lbp )

cuando el gráfico está completo (Para un gráfico completo E = O(V ² ). Pero para gráficos dispersos, el algoritmo funciona mucho mejor que el Algoritmo de Floyd Warshall ( https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp -16/?ref=lbp ).