El procedimiento paso a paso para obtener un valor óptimo (máximo o mínimo) de una función objetivo se denomina Algoritmo de Optimización .
Los algoritmos de optimización metaheurística son cada vez más populares en las aplicaciones de ingeniería porque:
- se basan en conceptos bastante simples y son fáciles de implementar
- no requieren información de gradiente
- puede pasar por alto los óptimos locales
- Se puede utilizar en una amplia gama de problemas que abarcan diferentes disciplinas.
Muchos académicos e investigadores han desarrollado varias metaheurísticas para abordar problemas de optimización complejos/no resueltos. Ejemplo: optimización de enjambre de partículas , optimización de lobo gris, optimización de colonia de hormigas , algoritmos genéticos , algoritmo de búsqueda de cuco, etc.
Este artículo tiene como objetivo presentar una nueva técnica de optimización metaheurística llamada algoritmo de optimización de ballenas (WOA)
Inspiración del algoritmo:
Algoritmo de optimización de ballenas (WOA): un algoritmo de optimización metaheurístico inspirado en la naturaleza que imita el comportamiento de caza de las ballenas jorobadas. El algoritmo está inspirado en la estrategia de caza de red de burbujas.
El comportamiento de alimentación de las ballenas jorobadas se denomina método de alimentación con red de burbujas. Las ballenas jorobadas prefieren cazar cardúmenes de krill o peces pequeños cerca de la superficie. Se ha observado que este forrajeo se realiza mediante la creación de burbujas distintivas a lo largo de un círculo o un camino en forma de ‘9’ como se muestra en la Fig. 1.
Dos maniobras asociadas con la alimentación con redes de burbujas son las «espirales ascendentes» y las «bucles dobles».
- En la maniobra de ‘espiral ascendente ‘, las ballenas jorobadas se sumergen alrededor de 12 m hacia abajo y luego comienzan a crear burbujas en forma de espiral alrededor de la presa y nadan hacia la superficie.
- La maniobra de ‘ doble bucle ‘ incluye tres etapas diferentes: bucle de coral, lobtail y bucle de captura

Figura 1: Comportamiento de alimentación con red de burbujas de las ballenas jorobadas.
Modelo matemático
La alimentación con red de burbujas es un comportamiento único que solo se puede observar en las ballenas jorobadas. En el algoritmo de optimización de ballenas (WOA), la maniobra de alimentación de la red de burbujas en espiral se modela matemáticamente para realizar la optimización.
- WOA simula el comportamiento de caza con el mejor agente de búsqueda o al azar para perseguir a la presa
- WOA usa una espiral para simular el mecanismo de ataque de red de burbujas de las ballenas jorobadas
Presa envolvente
Se supone que la mejor solución candidata actual está cerca de la presa objetivo y otras soluciones actualizan su posición hacia el mejor agente
(1)
(2)
Donde t indica la iteración actual, ![]() y
y ![]() son vectores de coeficientes,
son vectores de coeficientes, ![]() es el vector de posición de la mejor solución, e
es el vector de posición de la mejor solución, e ![]() indica el vector de posición de un lobo gris
indica el vector de posición de un lobo gris
(3)
(4)
Donde ![]() son vectores aleatorios en [0, 1].
son vectores aleatorios en [0, 1].
Método de ataque de red de burbujas (fase de explotación)
Para modelar matemáticamente el comportamiento de red de burbujas de las ballenas jorobadas, se diseñaron dos enfoques de la siguiente manera
- 1. Mecanismo envolvente de contracción
- Este comportamiento se logra al disminuir el valor de
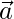 . a se reduce de 2 a 0 en el transcurso de las iteraciones.
. a se reduce de 2 a 0 en el transcurso de las iteraciones.
- Este comportamiento se logra al disminuir el valor de
- 2. Posición de actualización en espiral
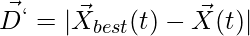
 (5)
(5) es un número aleatorio en [-1, 1]
es un número aleatorio en [-1, 1]
Buscar presa:
Las ballenas jorobadas buscan aleatoriamente según la posición de cada una
(6)
(7)
Algoritmo
Step1: Initialize the whales populationStep2: Calculate fitness of each search agent
= the best search agent Step3: while( t < maximum number of iterations ) for each search agent: Update
if(p<0.5): if(|A|<1): Update current agent by eq. (1) else: Select a random agent
update current agent by eq (7) else: update search agent by eq (5) end-for Check if any search agent goes beyond the search space and amend it Calculate fitness of each search agent Update
if there is a better solution t = t+1 end-while Step4: return
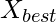
Referencias:
https://www.sciencedirect.com/science/article/pii/S0965997816300163
Publicación traducida automáticamente
Artículo escrito por shaadk7865 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA