En el aprendizaje por refuerzo, el agente o el tomador de decisiones aprende qué hacer, cómo mapear situaciones en acciones, para maximizar una señal de recompensa numérica. Al agente no se le dice explícitamente qué acciones tomar, sino que debe descubrir qué acción produce la mayor recompensa a través de prueba y error.
Problema de bandido con múltiples brazos
El problema del bandido con múltiples brazos se utiliza en el aprendizaje por refuerzo para formalizar la noción de toma de decisiones bajo incertidumbre. En un problema de bandidos con múltiples brazos, un agente (alumno) elige entre k acciones diferentes y recibe una recompensa basada en la acción elegida.
Los bandidos de múltiples brazos también se utilizan para describir conceptos fundamentales en el aprendizaje por refuerzo, como recompensas , intervalos de tiempo y valores .
Para seleccionar una acción por parte de un agente, asumimos que cada acción tiene una distribución separada de recompensasy hay al menos una acción que genera la máxima recompensa numérica. Así, la distribución de probabilidad de las recompensas correspondientes a cada acción es diferente y desconocida para el agente (tomador de decisiones). Por lo tanto, el objetivo del agente es identificar qué acción elegir para obtener la máxima recompensa después de un conjunto determinado de pruebas.
Valor de acción y estimación de valor de acción
Para que un agente decida qué acción produce la recompensa máxima, debemos definir el valor de realizar cada acción. Usamos el concepto de probabilidad para definir estos valores usando la función acción-valor.
El valor de seleccionar una acción se define como la recompensa esperada recibida al realizar esa acción de un conjunto de todas las acciones posibles. Dado que el agente no conoce el valor de seleccionar una acción, usamos el método de ‘promedio de muestra’ para estimar el valor de realizar una acción.

Exploración vs Explotación
La exploración permite que un agente mejore su conocimiento actual sobre cada acción, con la esperanza de generar un beneficio a largo plazo. Mejorar la precisión de los valores de acción estimados permite que un agente tome decisiones más informadas en el futuro.
La explotación , por otro lado, elige la acción codiciosa para obtener la mayor recompensa al explotar las estimaciones actuales del valor de la acción del agente. Pero al ser codicioso con respecto a las estimaciones del valor de la acción, es posible que en realidad no obtenga la mayor recompensa y conduzca a un comportamiento subóptimo.
Cuando un agente explora, obtiene estimaciones más precisas de los valores de acción. Y cuando explota, puede obtener más recompensa. Sin embargo, no puede optar por hacer ambas cosas simultáneamente, lo que también se denomina dilema de exploración-explotación.
Selección de acciones de
Epsilon-Greedy Epsilon-Greedy es un método simple para equilibrar la exploración y la explotación eligiendo aleatoriamente entre exploración y explotación.
El epsilon-codicioso, donde epsilon se refiere a la probabilidad de elegir explorar, explota la mayor parte del tiempo con una pequeña posibilidad de explorar.


Código: código Python para Epsilon-Greedy
# Import required libraries
import numpy as np
import matplotlib.pyplot as plt
# Define Action class
class Actions:
def __init__(self, m):
self.m = m
self.mean = 0
self.N = 0
# Choose a random action
def choose(self):
return np.random.randn() + self.m
# Update the action-value estimate
def update(self, x):
self.N += 1
self.mean = (1 - 1.0 / self.N)*self.mean + 1.0 / self.N * x
def run_experiment(m1, m2, m3, eps, N):
actions = [Actions(m1), Actions(m2), Actions(m3)]
data = np.empty(N)
for i in range(N):
# epsilon greedy
p = np.random.random()
if p < eps:
j = np.random.choice(3)
else:
j = np.argmax([a.mean for a in actions])
x = actions[j].choose()
actions[j].update(x)
# for the plot
data[i] = x
cumulative_average = np.cumsum(data) / (np.arange(N) + 1)
# plot moving average ctr
plt.plot(cumulative_average)
plt.plot(np.ones(N)*m1)
plt.plot(np.ones(N)*m2)
plt.plot(np.ones(N)*m3)
plt.xscale('log')
plt.show()
for a in actions:
print(a.mean)
return cumulative_average
if __name__ == '__main__':
c_1 = run_experiment(1.0, 2.0, 3.0, 0.1, 100000)
c_05 = run_experiment(1.0, 2.0, 3.0, 0.05, 100000)
c_01 = run_experiment(1.0, 2.0, 3.0, 0.01, 100000)
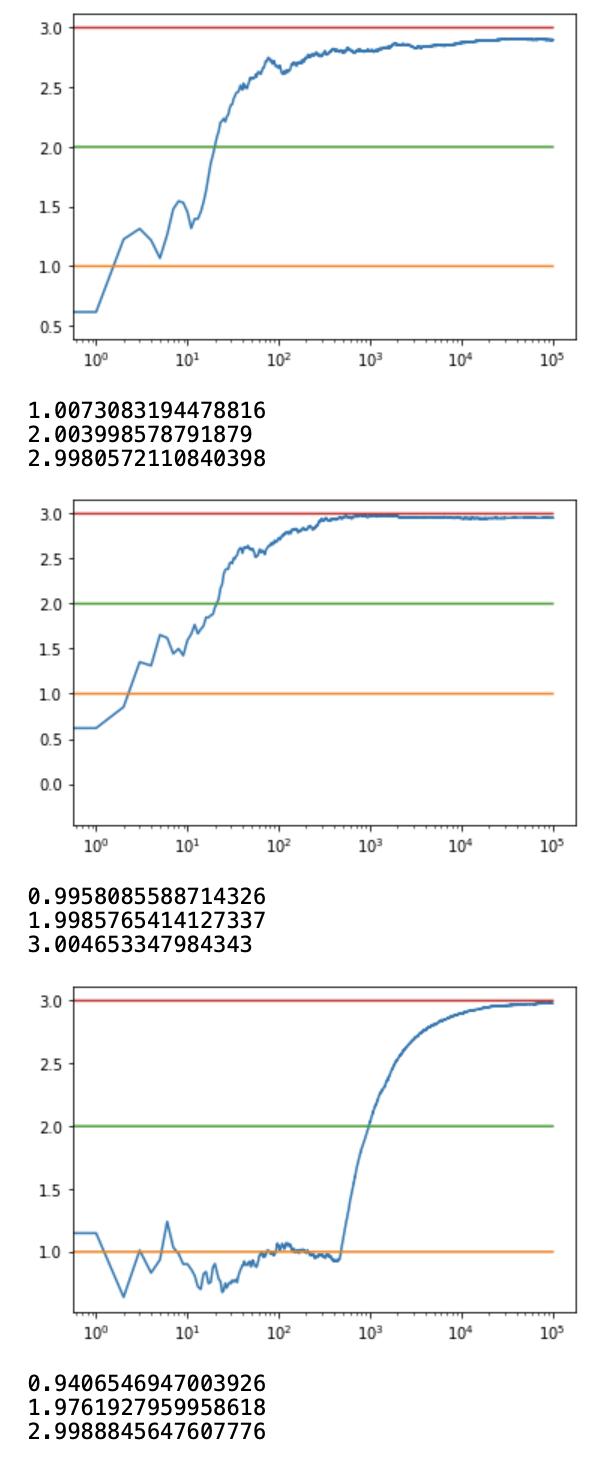
Producción:
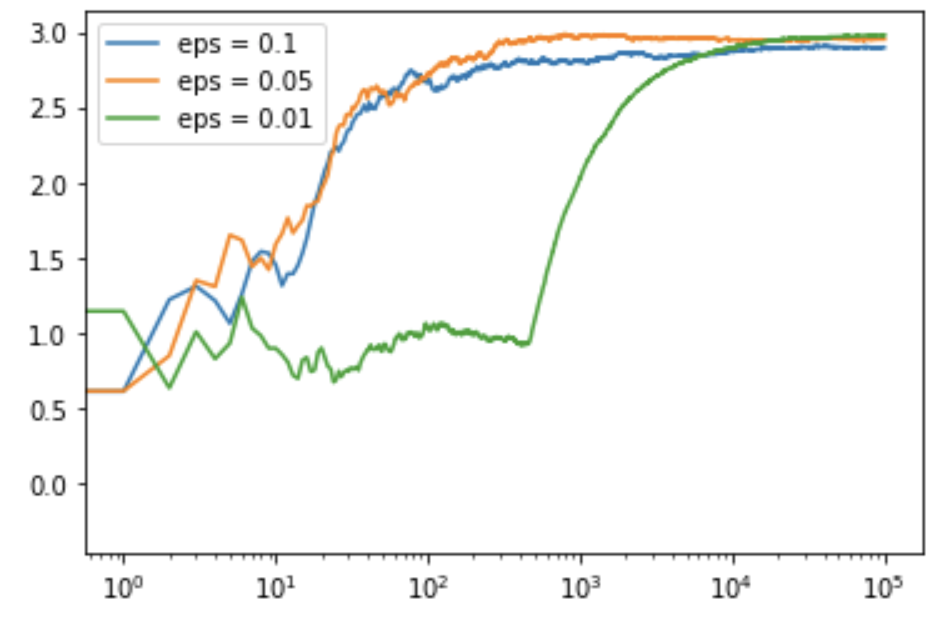
Code: Python code for getting the log output plot
# log scale plot
plt.plot(c_1, label ='eps = 0.1')
plt.plot(c_05, label ='eps = 0.05')
plt.plot(c_01, label ='eps = 0.01')
plt.legend()
plt.xscale('log')
plt.show()
Producción:
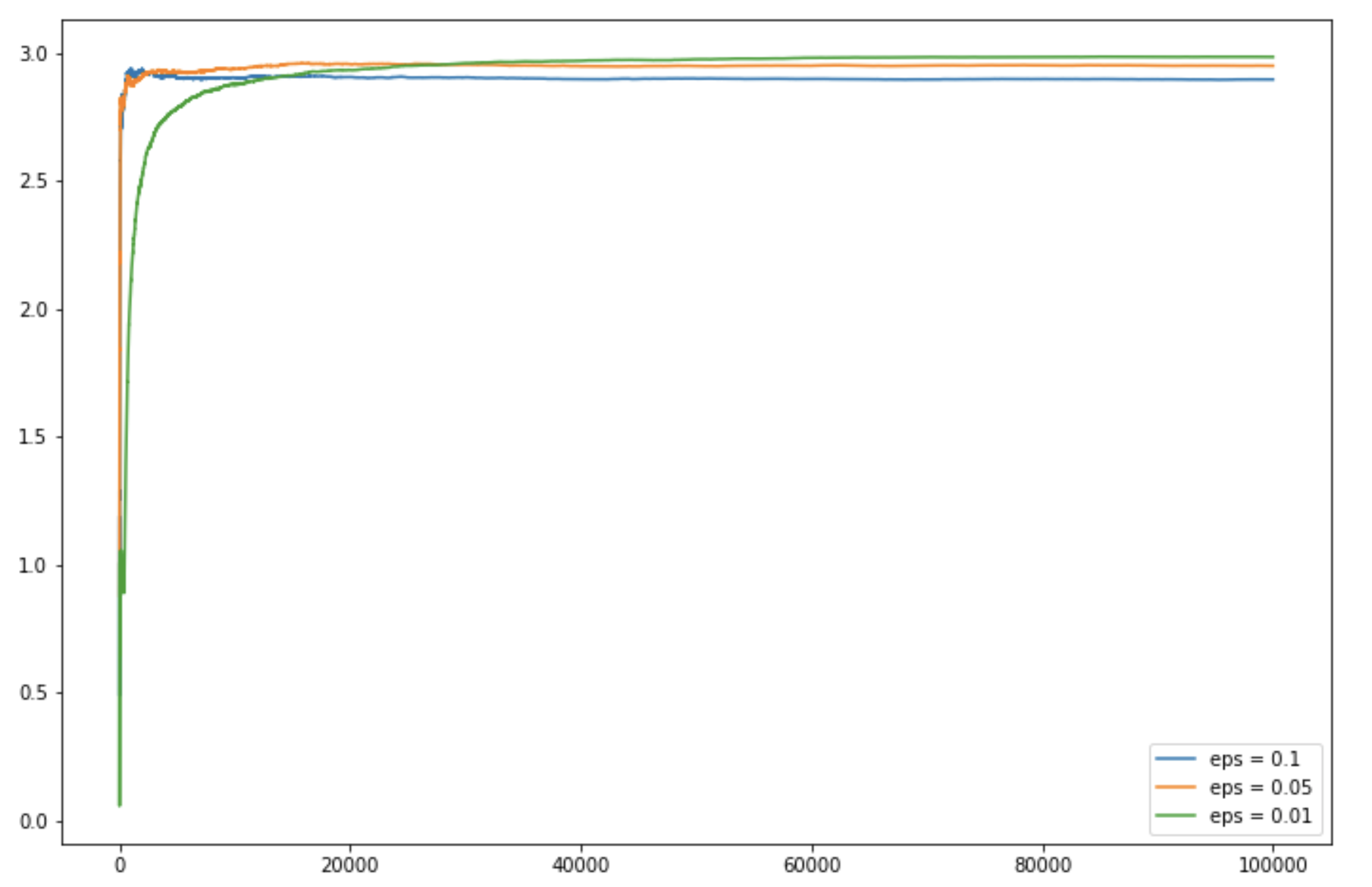
Código: código de Python para obtener el gráfico de salida lineal
# linear plot plt.figure(figsize = (12, 8)) plt.plot(c_1, label ='eps = 0.1') plt.plot(c_05, label ='eps = 0.05') plt.plot(c_01, label ='eps = 0.01') plt.legend() plt.show()
Producción: