Sean n agentes y n tareas. Se puede asignar cualquier agente para realizar cualquier tarea, lo que genera un costo que puede variar según la asignación de la tarea del agente. Se requiere realizar todas las tareas asignando exactamente un agente a cada tarea y exactamente una tarea a cada agente de tal manera que se minimice el costo total de la asignación. Ejemplo: trabaja como gerente para un fabricante de chips y actualmente tiene 3 personas en el camino reuniéndose con clientes. Sus vendedores están en Jaipur, Pune y Bangalore, y quiere que vuelen a otras tres ciudades: Delhi, Mumbai y Kerala. La siguiente tabla muestra el costo de los boletos de avión en INR entre las ciudades: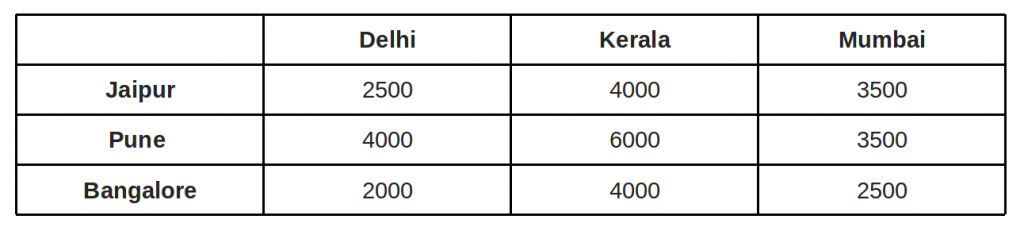 
La pregunta: ¿a dónde enviaría a cada uno de sus vendedores para minimizar la feria? Asignación posible: Costo = 11000 INR
Otro Asignación posible: Costo = 9500 INR y este es el mejor de los 3! asignaciones posibles. La solución de fuerza bruta es considerar que cada asignación posible implica una complejidad de Ω(n!) . El algoritmo húngaro, también conocido como algoritmo de asignación de Munkres , utiliza el siguiente teorema para la complejidad del tiempo de ejecución polinomial ( en el peor de los casos O(n 3 ) ) y la optimización garantizada: si se suma o se resta un número de todas las entradas de cualquier fila o columna de una array de costos, entonces una asignación óptima para la array de costos resultante también es una asignación óptima para la array de costos original.
Reducimos nuestra array de peso original para que contenga ceros, utilizando el teorema anterior. Tratamos de asignar tareas a los agentes de manera que cada agente esté haciendo solo una tarea y la penalización incurrida en cada caso sea cero . Núcleo del algoritmo (suponiendo array cuadrada):
- Para cada fila de la array, encuentre el elemento más pequeño y réstelo de cada elemento en su fila.
- Haga lo mismo (como en el paso 1) para todas las columnas.
- Cubra todos los ceros en la array utilizando el número mínimo de líneas horizontales y verticales.
- Prueba de Optimalidad: Si el número mínimo de líneas de cobertura es n, es posible una asignación óptima y hemos terminado. De lo contrario, si las líneas son menores que n, no hemos encontrado la asignación óptima y debemos continuar con el paso 5.
- Determine la entrada más pequeña no cubierta por ninguna línea. Reste esta entrada de cada fila descubierta y luego súmela a cada columna cubierta. Regrese al paso 3.
Explicación para el ejemplo simple anterior:
Below is the cost matrix of example given in above diagrams. 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, we have found the optimal assignment. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500
Un ejemplo que no conduce al valor óptimo en el primer intento: En el ejemplo anterior, la primera verificación de la optimización nos dio una solución. ¿Qué pasa si el número que cubre las líneas es menor que n?
cost matrix: 1500 4000 4500 2000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 1500, 2000 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 2500 3000 0 4000 1500 0 2000 500 Step 2: Subtract minimum of every column. 0, 2000 and 500 are subtracted from columns 1, 2 and 3 respectively. 0 500 2500 0 2000 1000 0 0 0 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we only need 2 lines to cover all zeroes, we have NOT found the optimal assignment. Step 5: We subtract the smallest uncovered entry from all uncovered rows. Smallest entry is 500. -500 0 2000 -500 1500 500 0 0 0 Then we add the smallest entry to all covered columns, we get 0 0 2000 0 1500 500 500 0 0 Now we return to Step 3:. Here we cover again using lines. and go to Step 4:. Since we need 3 lines to cover, we found the optimal solution. 1500 4000 4500 2000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 2000 + 2500 = 8500
C++
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
int cost[31][31]; //cost matrix
int n, max_match; //n workers and n jobs
int lx[31], ly[31]; //labels of X and Y parts
int xy[31]; //xy[x] - vertex that is matched with x,
int yx[31]; //yx[y] - vertex that is matched with y
bool S[31], T[31]; //sets S and T in algorithm
int slack[31]; //as in the algorithm description
int slackx[31]; //slackx[y] such a vertex, that
int prev_ious[31]; //array for memorizing alternating p
void init_labels()
{
memset(lx, 0, sizeof(lx));
memset(ly, 0, sizeof(ly));
for (int x = 0; x < n; x++)
for (int y = 0; y < n; y++)
lx[x] = max(lx[x], cost[x][y]);
}
void update_labels()
{
int x, y;
int delta = 99999999; //init delta as infinity
for (y = 0; y < n; y++) //calculate delta using slack
if (!T[y])
delta = min(delta, slack[y]);
for (x = 0; x < n; x++) //update X labels
if (S[x])
lx[x] -= delta;
for (y = 0; y < n; y++) //update Y labels
if (T[y])
ly[y] += delta;
for (y = 0; y < n; y++) //update slack array
if (!T[y])
slack[y] -= delta;
}
void add_to_tree(int x, int prev_iousx)
//x - current vertex,prev_iousx - vertex from X before x in the alternating path,
//so we add edges (prev_iousx, xy[x]), (xy[x], x)
{
S[x] = true; //add x to S
prev_ious[x] = prev_iousx; //we need this when augmenting
for (int y = 0; y < n; y++) //update slacks, because we add new vertex to S
if (lx[x] + ly[y] - cost[x][y] < slack[y])
{
slack[y] = lx[x] + ly[y] - cost[x][y];
slackx[y] = x;
}
}
void augment() //main function of the algorithm
{
if (max_match == n) return; //check whether matching is already perfect
int x, y, root; //just counters and root vertex
int q[31], wr = 0, rd = 0; //q - queue for bfs, wr,rd - write and read
//pos in queue
memset(S, false, sizeof(S)); //init set S
memset(T, false, sizeof(T)); //init set T
memset(prev_ious, -1, sizeof(prev_ious)); //init set prev_ious - for the alternating tree
for (x = 0; x < n; x++) //finding root of the tree
{
if (xy[x] == -1)
{
q[wr++] = root = x;
prev_ious[x] = -2;
S[x] = true;
break;
}
}
for (y = 0; y < n; y++) //initializing slack array
{
slack[y] = lx[root] + ly[y] - cost[root][y];
slackx[y] = root;
}
//second part of augment() function
while (true) //main cycle
{
while (rd < wr) //building tree with bfs cycle
{
x = q[rd++]; //current vertex from X part
for (y = 0; y < n; y++) //iterate through all edges in equality graph
if (cost[x][y] == lx[x] + ly[y] && !T[y])
{
if (yx[y] == -1) break; //an exposed vertex in Y found, so
//augmenting path exists!
T[y] = true; //else just add y to T,
q[wr++] = yx[y]; //add vertex yx[y], which is matched
//with y, to the queue
add_to_tree(yx[y], x); //add edges (x,y) and (y,yx[y]) to the tree
}
if (y < n)
break; //augmenting path found!
}
if (y < n)
break; //augmenting path found!
update_labels(); //augmenting path not found, so improve labeling
wr = rd = 0;
for (y = 0; y < n; y++)
//in this cycle we add edges that were added to the equality graph as a
//result of improving the labeling, we add edge (slackx[y], y) to the tree if
//and only if !T[y] && slack[y] == 0, also with this edge we add another one
//(y, yx[y]) or augment the matching, if y was exposed
if (!T[y] && slack[y] == 0)
{
if (yx[y] == -1) //exposed vertex in Y found - augmenting path exists!
{
x = slackx[y];
break;
}
else
{
T[y] = true; //else just add y to T,
if (!S[yx[y]])
{
q[wr++] = yx[y]; //add vertex yx[y], which is matched with
//y, to the queue
add_to_tree(yx[y], slackx[y]); //and add edges (x,y) and (y,
//yx[y]) to the tree
}
}
}
if (y < n) break; //augmenting path found!
}
if (y < n) //we found augmenting path!
{
max_match++; //increment matching
//in this cycle we inverse edges along augmenting path
for (int cx = x, cy = y, ty; cx != -2; cx = prev_ious[cx], cy = ty)
{
ty = xy[cx];
yx[cy] = cx;
xy[cx] = cy;
}
augment(); //recall function, go to step 1 of the algorithm
}
}//end of augment() function
int hungarian()
{
int ret = 0; //weight of the optimal matching
max_match = 0; //number of vertices in current matching
memset(xy, -1, sizeof(xy));
memset(yx, -1, sizeof(yx));
init_labels(); //step 0
augment(); //steps 1-3
for (int x = 0; x < n; x++) //forming answer there
ret += cost[x][xy[x]];
return ret;
}
int assignmentProblem(int Arr[], int N) {
n = N;
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
cost[i][j] = -1*Arr[i*n+j];
int ans = -1 * hungarian();
return ans;
}
};
int main()
{
int n=3;
int Arr[3*3]={1500,4000,4500,2000,6000,3500,2000,4000,2500}; /*1500 4000 4500
2000 6000 3500
2000 4000 2500*/
Solution ob;
cout<<ob.assignmentProblem(Arr,n)<<endl;
}
8500
En la próxima publicación, discutiremos la implementación del algoritmo anterior. La implementación requiere más pasos ya que necesitamos encontrar el número mínimo de líneas para cubrir todos los 0 usando un programa. Referencias: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY Este artículo es una contribución de Yash Varyani . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA