En el artículo , ya hemos discutido el algoritmo KMP para la búsqueda de patrones. En este artículo, se analiza un algoritmo KMP optimizado en tiempo real.
Del artículo anterior, se sabe que el algoritmo KMP (también conocido como Knuth-Morris-Pratt) preprocesa el patrón P y construye una función de falla F (también llamada lps[]) para almacenar la longitud del sufijo más largo del subpatrón P[1..l], que también es un prefijo de P, para l = 0 a m-1. Tenga en cuenta que el subpatrón comienza en el índice 1 porque un sufijo puede ser la propia string. Después de que ocurrió una discrepancia en el índice P[j], actualizamos j a F[j-1].
El algoritmo KMP original tiene una complejidad de tiempo de ejecución de O(M + N) y un espacio auxiliar O(M), donde N es el tamaño del texto de entrada y M es el tamaño del patrón. El paso de preprocesamiento cuesta O(M) tiempo. Es difícil lograr una complejidad de tiempo de ejecución mejor que eso, pero aun así podemos eliminar algunos turnos ineficientes.
Ineficiencias del algoritmo KMP original: considere el siguiente caso utilizando el algoritmo KMP original:
Entrada: T = “cabababcababaca”, P = “ababaca”
Salida: Encontrado en el índice 8
El prefijo propio más largo o lps[] para el caso de prueba anterior es {0, 0, 1, 2, 3, 0, 1}. Supongamos que el color rojo representa que se produce una falta de coincidencia, el color verde representa la verificación que omitimos. Por lo tanto, el proceso de búsqueda según el algoritmo KMP original ocurre de la siguiente manera:
Una cosa que se puede notar es que en el tercer, cuarto y quinto emparejamiento, el desajuste ocurre en la misma ubicación, T[7]. Si podemos omitir la cuarta y quinta coincidencia, entonces el algoritmo KMP original puede optimizarse aún más para responder a las consultas en tiempo real.
Optimización en tiempo real: el término en tiempo real en este caso se puede interpretar como verificar cada carácter en el texto T como máximo una vez. Nuestro objetivo en este caso es cambiar el patrón correctamente (al igual que lo hace el algoritmo KMP), pero no es necesario volver a verificar el carácter que no coincide. Es decir, para el mismo ejemplo anterior, el algoritmo KMP optimizado debería funcionar de la siguiente manera:
Enfoque: una forma de lograr el objetivo es modificar el proceso de preprocesamiento.
- Sea K el tamaño de las letras del patrón P . Construiremos una tabla de fallas para contener K funciones de fallas (es decir, lps[]).
- Cada función de falla en la tabla de fallas se asigna a un carácter (clave en la tabla de fallas) en el alfabeto del patrón P.
- Recuerde que la función de falla original F[l] (o lps[]) almacena la longitud del sufijo más largo de P[1..l], que también es un prefijo de P , para l = 0 a m-1, donde m es el tamaño del patrón.
- Si ocurre una discrepancia en T[i] y P[j] , el nuevo valor de j se actualizaría a F[j-1] y el contador ‘i’ no cambiaría.
- En nuestra nueva tabla de fallas FT[][] , si una función de falla F’ se asigna con un carácter c, F'[l] debería almacenar la longitud del sufijo más largo de P[1..l] + c (‘+ ‘ representa agregar), que también es un prefijo de P, para l = 0 a m-1.
- La intuición es hacer los cambios adecuados pero también dependiendo del personaje que no coincida. Aquí, el carácter c, que también es una clave en la tabla de fallas, es nuestra «suposición» sobre el carácter no coincidente en el texto T.
- Es decir, si el carácter no coincidente es c, ¿cómo deberíamos cambiar el patrón correctamente? Dado que estamos construyendo la tabla de fallas en el paso de preprocesamiento, tenemos que hacer suficientes conjeturas sobre el carácter no coincidente.
- Por lo tanto, el número de lps[] en la tabla de fallas es igual al tamaño del alfabeto del patrón, y cada valor, la función de falla, debe ser diferente con respecto a la clave, un carácter en P .
- Supongamos que ya hemos construido la tabla de fallas deseada. Sea FT[][] la tabla de fallas, T el texto, P el patrón.
- Luego, en el proceso de emparejamiento, si ocurre un desajuste en T[i] y P[j] (es decir, T[i] != P[j]):
- Si T[i] es un carácter en P , j se actualizará a FT[T[i]][j-1] , ‘ i ‘ se actualizará a ‘ i + 1 ‘. Estamos haciendo esto porque tenemos la garantía de que T[i] se iguala o se salta.
- Si T[i] no es un carácter, ‘j’ se actualizará a 0, ‘i’ se actualizará a ‘i + 1’.
- Tenga en cuenta que si no se produce una falta de coincidencia, el comportamiento es exactamente el mismo que el del algoritmo KMP original.
Tabla de fallas de construcción:
- Para construir la tabla de fallas FT[][], necesitaremos la función de fallas F(o lps[]) del algoritmo KMP original.
- Dado que F[l] nos dice la longitud del sufijo más largo del subpatrón P[1..l], que también es un prefijo de P, los valores almacenados en la tabla de fallas están un paso más allá.
- Es decir, para cualquier tecla t en la tabla de fallas FT[][], los valores almacenados en FT[t] son una función de falla que satisface el carácter ‘t’ y FT[t][l] almacena la longitud de la el sufijo más largo de un subpatrón P[1..l] + t(‘+’ significa agregar), que también es un prefijo de P, para l de 0 a m-1.
- F[l] ya ha garantizado que P[0..F[l]-1] es el sufijo más largo del subpatrón P[1..l], por lo que tendremos que comprobar si P[F[l] ] es t.
- Si es cierto, entonces podemos asignar FT[t][l] para que sea F[l] + 1, ya que tenemos la garantía de que P[0..F[l]] es el sufijo más largo del subpatrón P[1 ..l] + t.
- Si es falso, eso indica que P[F[l]] no es t. Es decir, no logramos la coincidencia en el carácter P[F[l]] con el carácter t, pero P[0..F[l]-1] coincide con un sufijo de P[1..l].
- Al tomar prestada la idea del algoritmo KMP, tal como calculamos la función de falla en el algoritmo KMP original, si la discrepancia ocurre en P[F[l]] con el carácter t no coincidente, nos gustaría actualizar la siguiente coincidencia que comienza en FT[ t][F[l]-1].
- Es decir, usamos la idea del algoritmo KMP para calcular la tabla de fallas. Tenga en cuenta que F[l] – 1 siempre es menor que l, por lo que cuando estamos calculando FT[t][l], FT[t][F[l] – 1] ya está listo para nosotros.
- Un caso especial es que si F[l] es 0 y P[F[l]] no es t, F[l] – 1 tiene un valor de -1, en este caso actualizaremos FT[t][l ] a 0. (es decir, no existe un sufijo de P[1..l] + t tal que sea un prefijo de P.)
- Como conclusión de la construcción de la tabla de fallas, cuando estemos calculando FT[t][l], para cualquier clave t y l de 0 a m-1, verificaremos:
If P[F[l]] is t, if yes: FT[t][l] <- F[l] + 1; if no: check if F[l] is 0, if yes: FT[t][l] <- 0; if no: FT[t][l] <- FT[t][F[t] - 1]; - El nuevo paso de preprocesamiento tiene una complejidad de tiempo de ejecución de O(
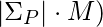 , donde
, donde 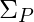 es el conjunto alfabético del patrón P, M es el tamaño de P.
es el conjunto alfabético del patrón P, M es el tamaño de P. - Todo el algoritmo KMP modificado tiene una complejidad de tiempo de ejecución de O(
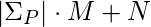 ). El uso del espacio auxiliar de O(
). El uso del espacio auxiliar de O( 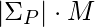 ).
). - El tiempo de ejecución y el uso del espacio parecen «peores» que el algoritmo KMP original. Sin embargo, si estamos buscando el mismo patrón en varios textos o el conjunto alfabético del patrón es pequeño, ya que el paso de preprocesamiento solo debe realizarse una vez y cada carácter del texto se comparará como máximo una vez (en tiempo real) . Por lo tanto, es más eficiente que el algoritmo KMP original y es bueno en la práctica.
Estos son los resultados deseados del ejemplo anterior, los resultados incluyen la tabla de fallas para una mejor ilustración.
Ejemplos:
Entrada: T = “cabababcababaca”, P = “ababaca”
Salida: Tabla de fallas:
Valor clave
‘a’ [1 1 1 3 1 1 1]
‘b’ [0 0 2 0 4 0 2]
‘c’ [0 0 0 0 0 0 0]
Patrón encontrado en el índice 8
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to implement a// real time optimized KMP// algorithm for pattern searching #include <iostream>#include <set>#include <string>#include <unordered_map> using std::string;using std::unordered_map;using std::set;using std::cout; // Function to print// an array of length lenvoid printArr(int* F, int len, char name){ cout << '(' << name << ')' << "contain: ["; // Loop to iterate through // and print the array for (int i = 0; i < len; i++) { cout << F[i] << " "; } cout << "]\n";} // Function to print a table.// len is the length of each array// in the map.void printTable( unordered_map<char, int*>& FT, int len){ cout << "Failure Table: {\n"; // Iterating through the table // and printing it for (auto& pair : FT) { printArr(pair.second, len, pair.first); } cout << "}\n";} // Function to construct// the failure function// corresponding to the patternvoid constructFailureFunction( string& P, int* F){ // P is the pattern, // F is the FailureFunction // assume F has length m, // where m is the size of P int len = P.size(); // F[0] must have the value 0 F[0] = 0; // The index, we are parsing P[1..j] int j = 1; int l = 0; // Loop to iterate through the // pattern while (j < len) { // Computing the failure function or // lps[] similar to KMP Algorithm if (P[j] == P[l]) { l++; F[j] = l; j++; } else if (l > 0) { l = F[l - 1]; } else { F[j] = 0; j++; } }} // Function to construct the failure table.// P is the pattern, F is the original// failure function. The table is stored in// FT[][]void constructFailureTable( string& P, set<char>& pattern_alphabet, int* F, unordered_map<char, int*>& FT){ int len = P.size(); // T is the char where we mismatched for (char t : pattern_alphabet) { // Allocate an array FT[t] = new int[len]; int l = 0; while (l < len) { if (P[F[l]] == t) // Old failure function gives // a good shifting FT[t][l] = F[l] + 1; else { // Move to the next char if // the entry in the failure // function is 0 if (F[l] == 0) FT[t][l] = 0; // Fill the table if F[l] > 0 else FT[t][l] = FT[t][F[l] - 1]; } l++; } }} // Function to implement the realtime// optimized KMP algorithm for// pattern searching. T is the text// we are searching on and// P is the pattern we are searching forvoid KMP(string& T, string& P, set<char>& pattern_alphabet){ // Size of the pattern int m = P.size(); // Size of the text int n = T.size(); // Initialize the Failure Function int F[m]; // Constructing the failure function // using KMP algorithm constructFailureFunction(P, F); printArr(F, m, 'F'); unordered_map<char, int*> FT; // Construct the failure table and // store it in FT[][] constructFailureTable( P, pattern_alphabet, F, FT); printTable(FT, m); // The starting index will be when // the first match occurs int found_index = -1; // Variable to iterate over the // indices in Text T int i = 0; // Variable to iterate over the // indices in Pattern P int j = 0; // Loop to iterate over the text while (i < n) { if (P[j] == T[i]) { // Matched the last character in P if (j == m - 1) { found_index = i - m + 1; break; } else { i++; j++; } } else { if (j > 0) { // T[i] is not in P's alphabet if (FT.find(T[i]) == FT.end()) // Begin a new // matching process j = 0; else j = FT[T[i]][j - 1]; // Update 'j' to be the length of // the longest suffix of P[1..j] // which is also a prefix of P i++; } else i++; } } // Printing the index at which // the pattern is found if (found_index != -1) cout << "Found at index " << found_index << '\n'; else cout << "Not Found \n"; for (char t : pattern_alphabet) // Deallocate the arrays in FT delete[] FT[t]; return;} // Driver codeint main(){ string T = "cabababcababaca"; string P = "ababaca"; set<char> pattern_alphabet = { 'a', 'b', 'c' }; KMP(T, P, pattern_alphabet);} |
(F)contain: [0 0 1 2 3 0 1 ]
Failure Table: {
(c)contain: [0 0 0 0 0 0 0 ]
(a)contain: [1 1 1 3 1 1 1 ]
(b)contain: [0 0 2 0 4 0 2 ]
}
Found at index 8
Nota: El código fuente anterior encontrará la primera aparición del patrón. Con una ligera modificación, se puede utilizar para encontrar todas las ocurrencias.
Complejidad del tiempo:
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA