Prerrequisitos: Algoritmo Minimax en Teoría de Juegos , Función de Evaluación en Teoría de Juegos
Combinemos lo que hemos aprendido hasta ahora sobre minimax y la función de evaluación para escribir una IA (Inteligencia Artificial) Tic-Tac-Toe adecuada que juegue un juego perfecto. Esta IA considerará todos los escenarios posibles y hará el movimiento más óptimo.
Encontrar el mejor movimiento:
Presentaremos una nueva función llamada findBestMove() . Esta función evalúa todos los movimientos disponibles usando minimax() y luego devuelve el mejor movimiento que puede hacer el maximizador. El pseudocódigo es el siguiente:
function findBestMove(board):
bestMove = NULL
for each move in board :
if current move is better than bestMove
bestMove = current move
return bestMove
minimax :
Para verificar si el movimiento actual es mejor o no que el mejor movimiento, tomamos la ayuda de la función minimax() que considerará todas las formas posibles en que puede ir el juego y devuelve el mejor valor para ese movimiento, asumiendo que el oponente también juega de manera óptima
El código para el maximizador y el minimizador en la función minimax() es similar a findBestMove() , la única diferencia es que, en lugar de devolver un movimiento, devolverá un valor. Aquí está el pseudocódigo:
function minimax(board, depth, isMaximizingPlayer):
if current board state is a terminal state :
return value of the board
if isMaximizingPlayer :
bestVal = -INFINITY
for each move in board :
value = minimax(board, depth+1, false)
bestVal = max( bestVal, value)
return bestVal
else :
bestVal = +INFINITY
for each move in board :
value = minimax(board, depth+1, true)
bestVal = min( bestVal, value)
return bestVal
Comprobando el estado de GameOver:
Para verificar si el juego ha terminado y para asegurarnos de que no quedan movimientos, usamos la función isMovesLeft() . Es una función simple y directa que verifica si un movimiento está disponible o no y devuelve verdadero o falso, respectivamente. El pseudocódigo es el siguiente:
function isMovesLeft(board):
for each cell in board:
if current cell is empty:
return true
return false
Haciendo nuestra IA más inteligente:
Un paso final es hacer que nuestra IA sea un poco más inteligente. A pesar de que la siguiente IA funciona perfectamente, puede optar por hacer un movimiento que resulte en una victoria más lenta o una derrota más rápida. Tomemos un ejemplo y expliquemos.
Suponga que hay 2 formas posibles para que X gane el juego desde un estado dado del tablero.
- Movimiento: X puede ganar en 2 movimientos
- Movimiento: X puede ganar en 4 movimientos
Nuestra función de evaluación devolverá un valor de +10 tanto para movimientos como para . Aunque el movimiento es mejor porque asegura una victoria más rápida, nuestra IA puede elegir a veces. Para superar este problema restamos el valor de profundidad de la puntuación evaluada. Esto significa que, en caso de victoria, elegirá la victoria que requiere la menor cantidad de movimientos y, en caso de pérdida, intentará prolongar el juego y jugar tantos movimientos como sea posible. Entonces el nuevo valor evaluado será
- Mover tendrá un valor de +10 – 2 = 8
- Mover tendrá un valor de +10 – 4 = 6
Ahora, dado que el movimiento tiene una puntuación más alta en comparación con el movimiento, nuestra IA elegirá mover sobre mover. Lo mismo debe aplicarse al minimizador. En lugar de restar la profundidad, sumamos el valor de profundidad como el minimizador siempre trata de obtener, un valor tan negativo como sea posible. Podemos restar la profundidad ya sea dentro de la función de evaluación o fuera de ella. Cualquier lugar está bien. He optado por hacerlo fuera de la función. La implementación del pseudocódigo es la siguiente.
if maximizer has won:
return WIN_SCORE – depth
else if minimizer has won:
return LOOSE_SCORE + depth
A continuación se muestra la implementación de la idea anterior.
C++
// C++ program to find the next optimal move for
// a player
#include<bits/stdc++.h>
using namespace std;
struct Move
{
int row, col;
};
char player = 'x', opponent = 'o';
// This function returns true if there are moves
// remaining on the board. It returns false if
// there are no moves left to play.
bool isMovesLeft(char board[3][3])
{
for (int i = 0; i<3; i++)
for (int j = 0; j<3; j++)
if (board[i][j]=='_')
return true;
return false;
}
// This is the evaluation function as discussed
// in the previous article ( http://goo.gl/sJgv68 )
int evaluate(char b[3][3])
{
// Checking for Rows for X or O victory.
for (int row = 0; row<3; row++)
{
if (b[row][0]==b[row][1] &&
b[row][1]==b[row][2])
{
if (b[row][0]==player)
return +10;
else if (b[row][0]==opponent)
return -10;
}
}
// Checking for Columns for X or O victory.
for (int col = 0; col<3; col++)
{
if (b[0][col]==b[1][col] &&
b[1][col]==b[2][col])
{
if (b[0][col]==player)
return +10;
else if (b[0][col]==opponent)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (b[0][0]==b[1][1] && b[1][1]==b[2][2])
{
if (b[0][0]==player)
return +10;
else if (b[0][0]==opponent)
return -10;
}
if (b[0][2]==b[1][1] && b[1][1]==b[2][0])
{
if (b[0][2]==player)
return +10;
else if (b[0][2]==opponent)
return -10;
}
// Else if none of them have won then return 0
return 0;
}
// This is the minimax function. It considers all
// the possible ways the game can go and returns
// the value of the board
int minimax(char board[3][3], int depth, bool isMax)
{
int score = evaluate(board);
// If Maximizer has won the game return his/her
// evaluated score
if (score == 10)
return score;
// If Minimizer has won the game return his/her
// evaluated score
if (score == -10)
return score;
// If there are no more moves and no winner then
// it is a tie
if (isMovesLeft(board)==false)
return 0;
// If this maximizer's move
if (isMax)
{
int best = -1000;
// Traverse all cells
for (int i = 0; i<3; i++)
{
for (int j = 0; j<3; j++)
{
// Check if cell is empty
if (board[i][j]=='_')
{
// Make the move
board[i][j] = player;
// Call minimax recursively and choose
// the maximum value
best = max( best,
minimax(board, depth+1, !isMax) );
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
// If this minimizer's move
else
{
int best = 1000;
// Traverse all cells
for (int i = 0; i<3; i++)
{
for (int j = 0; j<3; j++)
{
// Check if cell is empty
if (board[i][j]=='_')
{
// Make the move
board[i][j] = opponent;
// Call minimax recursively and choose
// the minimum value
best = min(best,
minimax(board, depth+1, !isMax));
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
}
// This will return the best possible move for the player
Move findBestMove(char board[3][3])
{
int bestVal = -1000;
Move bestMove;
bestMove.row = -1;
bestMove.col = -1;
// Traverse all cells, evaluate minimax function for
// all empty cells. And return the cell with optimal
// value.
for (int i = 0; i<3; i++)
{
for (int j = 0; j<3; j++)
{
// Check if cell is empty
if (board[i][j]=='_')
{
// Make the move
board[i][j] = player;
// compute evaluation function for this
// move.
int moveVal = minimax(board, 0, false);
// Undo the move
board[i][j] = '_';
// If the value of the current move is
// more than the best value, then update
// best/
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
printf("The value of the best Move is : %d\n\n",
bestVal);
return bestMove;
}
// Driver code
int main()
{
char board[3][3] =
{
{ 'x', 'o', 'x' },
{ 'o', 'o', 'x' },
{ '_', '_', '_' }
};
Move bestMove = findBestMove(board);
printf("The Optimal Move is :\n");
printf("ROW: %d COL: %d\n\n", bestMove.row,
bestMove.col );
return 0;
}
Java
// Java program to find the
// next optimal move for a player
class GFG
{
static class Move
{
int row, col;
};
static char player = 'x', opponent = 'o';
// This function returns true if there are moves
// remaining on the board. It returns false if
// there are no moves left to play.
static Boolean isMovesLeft(char board[][])
{
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
if (board[i][j] == '_')
return true;
return false;
}
// This is the evaluation function as discussed
// in the previous article ( http://goo.gl/sJgv68 )
static int evaluate(char b[][])
{
// Checking for Rows for X or O victory.
for (int row = 0; row < 3; row++)
{
if (b[row][0] == b[row][1] &&
b[row][1] == b[row][2])
{
if (b[row][0] == player)
return +10;
else if (b[row][0] == opponent)
return -10;
}
}
// Checking for Columns for X or O victory.
for (int col = 0; col < 3; col++)
{
if (b[0][col] == b[1][col] &&
b[1][col] == b[2][col])
{
if (b[0][col] == player)
return +10;
else if (b[0][col] == opponent)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (b[0][0] == b[1][1] && b[1][1] == b[2][2])
{
if (b[0][0] == player)
return +10;
else if (b[0][0] == opponent)
return -10;
}
if (b[0][2] == b[1][1] && b[1][1] == b[2][0])
{
if (b[0][2] == player)
return +10;
else if (b[0][2] == opponent)
return -10;
}
// Else if none of them have won then return 0
return 0;
}
// This is the minimax function. It considers all
// the possible ways the game can go and returns
// the value of the board
static int minimax(char board[][],
int depth, Boolean isMax)
{
int score = evaluate(board);
// If Maximizer has won the game
// return his/her evaluated score
if (score == 10)
return score;
// If Minimizer has won the game
// return his/her evaluated score
if (score == -10)
return score;
// If there are no more moves and
// no winner then it is a tie
if (isMovesLeft(board) == false)
return 0;
// If this maximizer's move
if (isMax)
{
int best = -1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j]=='_')
{
// Make the move
board[i][j] = player;
// Call minimax recursively and choose
// the maximum value
best = Math.max(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
// If this minimizer's move
else
{
int best = 1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == '_')
{
// Make the move
board[i][j] = opponent;
// Call minimax recursively and choose
// the minimum value
best = Math.min(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
}
// This will return the best possible
// move for the player
static Move findBestMove(char board[][])
{
int bestVal = -1000;
Move bestMove = new Move();
bestMove.row = -1;
bestMove.col = -1;
// Traverse all cells, evaluate minimax function
// for all empty cells. And return the cell
// with optimal value.
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == '_')
{
// Make the move
board[i][j] = player;
// compute evaluation function for this
// move.
int moveVal = minimax(board, 0, false);
// Undo the move
board[i][j] = '_';
// If the value of the current move is
// more than the best value, then update
// best/
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
System.out.printf("The value of the best Move " +
"is : %d\n\n", bestVal);
return bestMove;
}
// Driver code
public static void main(String[] args)
{
char board[][] = {{ 'x', 'o', 'x' },
{ 'o', 'o', 'x' },
{ '_', '_', '_' }};
Move bestMove = findBestMove(board);
System.out.printf("The Optimal Move is :\n");
System.out.printf("ROW: %d COL: %d\n\n",
bestMove.row, bestMove.col );
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 program to find the next optimal move for a player
player, opponent = 'x', 'o'
# This function returns true if there are moves
# remaining on the board. It returns false if
# there are no moves left to play.
def isMovesLeft(board) :
for i in range(3) :
for j in range(3) :
if (board[i][j] == '_') :
return True
return False
# This is the evaluation function as discussed
# in the previous article ( http://goo.gl/sJgv68 )
def evaluate(b) :
# Checking for Rows for X or O victory.
for row in range(3) :
if (b[row][0] == b[row][1] and b[row][1] == b[row][2]) :
if (b[row][0] == player) :
return 10
elif (b[row][0] == opponent) :
return -10
# Checking for Columns for X or O victory.
for col in range(3) :
if (b[0][col] == b[1][col] and b[1][col] == b[2][col]) :
if (b[0][col] == player) :
return 10
elif (b[0][col] == opponent) :
return -10
# Checking for Diagonals for X or O victory.
if (b[0][0] == b[1][1] and b[1][1] == b[2][2]) :
if (b[0][0] == player) :
return 10
elif (b[0][0] == opponent) :
return -10
if (b[0][2] == b[1][1] and b[1][1] == b[2][0]) :
if (b[0][2] == player) :
return 10
elif (b[0][2] == opponent) :
return -10
# Else if none of them have won then return 0
return 0
# This is the minimax function. It considers all
# the possible ways the game can go and returns
# the value of the board
def minimax(board, depth, isMax) :
score = evaluate(board)
# If Maximizer has won the game return his/her
# evaluated score
if (score == 10) :
return score
# If Minimizer has won the game return his/her
# evaluated score
if (score == -10) :
return score
# If there are no more moves and no winner then
# it is a tie
if (isMovesLeft(board) == False) :
return 0
# If this maximizer's move
if (isMax) :
best = -1000
# Traverse all cells
for i in range(3) :
for j in range(3) :
# Check if cell is empty
if (board[i][j]=='_') :
# Make the move
board[i][j] = player
# Call minimax recursively and choose
# the maximum value
best = max( best, minimax(board,
depth + 1,
not isMax) )
# Undo the move
board[i][j] = '_'
return best
# If this minimizer's move
else :
best = 1000
# Traverse all cells
for i in range(3) :
for j in range(3) :
# Check if cell is empty
if (board[i][j] == '_') :
# Make the move
board[i][j] = opponent
# Call minimax recursively and choose
# the minimum value
best = min(best, minimax(board, depth + 1, not isMax))
# Undo the move
board[i][j] = '_'
return best
# This will return the best possible move for the player
def findBestMove(board) :
bestVal = -1000
bestMove = (-1, -1)
# Traverse all cells, evaluate minimax function for
# all empty cells. And return the cell with optimal
# value.
for i in range(3) :
for j in range(3) :
# Check if cell is empty
if (board[i][j] == '_') :
# Make the move
board[i][j] = player
# compute evaluation function for this
# move.
moveVal = minimax(board, 0, False)
# Undo the move
board[i][j] = '_'
# If the value of the current move is
# more than the best value, then update
# best/
if (moveVal > bestVal) :
bestMove = (i, j)
bestVal = moveVal
print("The value of the best Move is :", bestVal)
print()
return bestMove
# Driver code
board = [
[ 'x', 'o', 'x' ],
[ 'o', 'o', 'x' ],
[ '_', '_', '_' ]
]
bestMove = findBestMove(board)
print("The Optimal Move is :")
print("ROW:", bestMove[0], " COL:", bestMove[1])
# This code is contributed by divyesh072019
C#
// C# program to find the
// next optimal move for a player
using System;
using System.Collections.Generic;
class GFG
{
class Move
{
public int row, col;
};
static char player = 'x', opponent = 'o';
// This function returns true if there are moves
// remaining on the board. It returns false if
// there are no moves left to play.
static Boolean isMovesLeft(char [,]board)
{
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
if (board[i, j] == '_')
return true;
return false;
}
// This is the evaluation function as discussed
// in the previous article ( http://goo.gl/sJgv68 )
static int evaluate(char [,]b)
{
// Checking for Rows for X or O victory.
for (int row = 0; row < 3; row++)
{
if (b[row, 0] == b[row, 1] &&
b[row, 1] == b[row, 2])
{
if (b[row, 0] == player)
return +10;
else if (b[row, 0] == opponent)
return -10;
}
}
// Checking for Columns for X or O victory.
for (int col = 0; col < 3; col++)
{
if (b[0, col] == b[1, col] &&
b[1, col] == b[2, col])
{
if (b[0, col] == player)
return +10;
else if (b[0, col] == opponent)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (b[0, 0] == b[1, 1] && b[1, 1] == b[2, 2])
{
if (b[0, 0] == player)
return +10;
else if (b[0, 0] == opponent)
return -10;
}
if (b[0, 2] == b[1, 1] && b[1, 1] == b[2, 0])
{
if (b[0, 2] == player)
return +10;
else if (b[0, 2] == opponent)
return -10;
}
// Else if none of them have won then return 0
return 0;
}
// This is the minimax function. It considers all
// the possible ways the game can go and returns
// the value of the board
static int minimax(char [,]board,
int depth, Boolean isMax)
{
int score = evaluate(board);
// If Maximizer has won the game
// return his/her evaluated score
if (score == 10)
return score;
// If Minimizer has won the game
// return his/her evaluated score
if (score == -10)
return score;
// If there are no more moves and
// no winner then it is a tie
if (isMovesLeft(board) == false)
return 0;
// If this maximizer's move
if (isMax)
{
int best = -1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i, j] == '_')
{
// Make the move
board[i, j] = player;
// Call minimax recursively and choose
// the maximum value
best = Math.Max(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i, j] = '_';
}
}
}
return best;
}
// If this minimizer's move
else
{
int best = 1000;
// Traverse all cells
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i, j] == '_')
{
// Make the move
board[i, j] = opponent;
// Call minimax recursively and choose
// the minimum value
best = Math.Min(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i, j] = '_';
}
}
}
return best;
}
}
// This will return the best possible
// move for the player
static Move findBestMove(char [,]board)
{
int bestVal = -1000;
Move bestMove = new Move();
bestMove.row = -1;
bestMove.col = -1;
// Traverse all cells, evaluate minimax function
// for all empty cells. And return the cell
// with optimal value.
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i, j] == '_')
{
// Make the move
board[i, j] = player;
// compute evaluation function for this
// move.
int moveVal = minimax(board, 0, false);
// Undo the move
board[i, j] = '_';
// If the value of the current move is
// more than the best value, then update
// best/
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
Console.Write("The value of the best Move " +
"is : {0}\n\n", bestVal);
return bestMove;
}
// Driver code
public static void Main(String[] args)
{
char [,]board = {{ 'x', 'o', 'x' },
{ 'o', 'o', 'x' },
{ '_', '_', '_' }};
Move bestMove = findBestMove(board);
Console.Write("The Optimal Move is :\n");
Console.Write("ROW: {0} COL: {1}\n\n",
bestMove.row, bestMove.col );
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to find the
// next optimal move for a player
class Move
{
constructor()
{
let row,col;
}
}
let player = 'x', opponent = 'o';
// This function returns true if there are moves
// remaining on the board. It returns false if
// there are no moves left to play.
function isMovesLeft(board)
{
for(let i = 0; i < 3; i++)
for(let j = 0; j < 3; j++)
if (board[i][j] == '_')
return true;
return false;
}
// This is the evaluation function as discussed
// in the previous article ( http://goo.gl/sJgv68 )
function evaluate(b)
{
// Checking for Rows for X or O victory.
for(let row = 0; row < 3; row++)
{
if (b[row][0] == b[row][1] &&
b[row][1] == b[row][2])
{
if (b[row][0] == player)
return +10;
else if (b[row][0] == opponent)
return -10;
}
}
// Checking for Columns for X or O victory.
for(let col = 0; col < 3; col++)
{
if (b[0][col] == b[1][col] &&
b[1][col] == b[2][col])
{
if (b[0][col] == player)
return +10;
else if (b[0][col] == opponent)
return -10;
}
}
// Checking for Diagonals for X or O victory.
if (b[0][0] == b[1][1] && b[1][1] == b[2][2])
{
if (b[0][0] == player)
return +10;
else if (b[0][0] == opponent)
return -10;
}
if (b[0][2] == b[1][1] &&
b[1][1] == b[2][0])
{
if (b[0][2] == player)
return +10;
else if (b[0][2] == opponent)
return -10;
}
// Else if none of them have
// won then return 0
return 0;
}
// This is the minimax function. It
// considers all the possible ways
// the game can go and returns the
// value of the board
function minimax(board, depth, isMax)
{
let score = evaluate(board);
// If Maximizer has won the game
// return his/her evaluated score
if (score == 10)
return score;
// If Minimizer has won the game
// return his/her evaluated score
if (score == -10)
return score;
// If there are no more moves and
// no winner then it is a tie
if (isMovesLeft(board) == false)
return 0;
// If this maximizer's move
if (isMax)
{
let best = -1000;
// Traverse all cells
for(let i = 0; i < 3; i++)
{
for(let j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j]=='_')
{
// Make the move
board[i][j] = player;
// Call minimax recursively
// and choose the maximum value
best = Math.max(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
// If this minimizer's move
else
{
let best = 1000;
// Traverse all cells
for(let i = 0; i < 3; i++)
{
for(let j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == '_')
{
// Make the move
board[i][j] = opponent;
// Call minimax recursively and
// choose the minimum value
best = Math.min(best, minimax(board,
depth + 1, !isMax));
// Undo the move
board[i][j] = '_';
}
}
}
return best;
}
}
// This will return the best possible
// move for the player
function findBestMove(board)
{
let bestVal = -1000;
let bestMove = new Move();
bestMove.row = -1;
bestMove.col = -1;
// Traverse all cells, evaluate
// minimax function for all empty
// cells. And return the cell
// with optimal value.
for(let i = 0; i < 3; i++)
{
for(let j = 0; j < 3; j++)
{
// Check if cell is empty
if (board[i][j] == '_')
{
// Make the move
board[i][j] = player;
// compute evaluation function
// for this move.
let moveVal = minimax(board, 0, false);
// Undo the move
board[i][j] = '_';
// If the value of the current move
// is more than the best value, then
// update best
if (moveVal > bestVal)
{
bestMove.row = i;
bestMove.col = j;
bestVal = moveVal;
}
}
}
}
document.write("The value of the best Move " +
"is : ", bestVal + "<br><br>");
return bestMove;
}
// Driver code
let board = [ [ 'x', 'o', 'x' ],
[ 'o', 'o', 'x' ],
[ '_', '_', '_' ] ];
let bestMove = findBestMove(board);
document.write("The Optimal Move is :<br>");
document.write("ROW: " + bestMove.row +
" COL: "+ bestMove.col + "<br>");
// This code is contributed by rag2127
</script>
Producción :
The value of the best Move is : 10 The Optimal Move is : ROW: 2 COL: 2
Explicación :
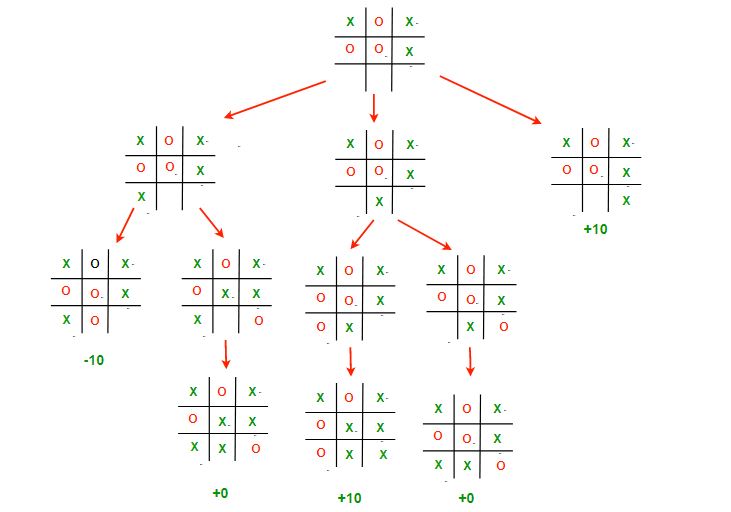
Esta imagen muestra todos los caminos posibles que el juego puede tomar desde el estado del tablero raíz. A menudo se le llama el Árbol del Juego .
Los 3 escenarios posibles en el ejemplo anterior son:
- Movimiento a la izquierda : si X juega [2,0]. Entonces O jugará [2,1] y ganará el juego. El valor de este movimiento es -10
- Movimiento medio : si X juega [2,1]. Entonces O jugará [2,2] que dibuja el juego. El valor de este movimiento es 0
- Movimiento a la derecha : si X juega [2,2]. Entonces él ganará el juego. El valor de este movimiento es +10;
Recuerde, aunque X tiene la posibilidad de ganar si juega el movimiento medio, O nunca dejará que eso suceda y elegirá tablas en su lugar.
Por lo tanto, la mejor opción para X es jugar [2,2], lo que le garantizará una victoria.
Alentamos a nuestros lectores a que intenten dar varios aportes y comprender por qué la IA elige realizar ese movimiento. Minimax puede confundir a los programadores, ya que piensa en varios movimientos por adelantado y, en ocasiones, es muy difícil de depurar. Recuerde que esta implementación del algoritmo minimax se puede aplicar a cualquier juego de mesa de 2 jugadores con algunos cambios menores en la estructura del tablero y en cómo iteramos a través de los movimientos. Además, a veces es imposible que minimax calcule todos los estados de juego posibles para juegos complejos como el ajedrez. Por lo tanto, solo calculamos hasta cierta profundidad y usamos la función de evaluación para calcular el valor del tablero.
Estén atentos al artículo de las próximas semanas en el que hablaremos sobre la poda alfa-beta que puede mejorar drásticamente el tiempo que tarda minimax en atravesar un árbol de juego.
Este artículo es una contribución de Akshay L Aradhya . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA