- Pregunta 1: ¿Cuál de los siguientes es el valor de T 3 (n) donde T 3 (n) se define como T 3 (n) = 5*T 3 (n-1) – 4*T 3 (n-2)
- C 1 * 5 norte + C 2 * 4 norte
- do 1 + do 2 *4 norte
- C 1 * 2 norte + C 2 * 4 norte
- C 1 * 5 norte + C 2 * (-4) norte
Respuesta: 2
Explicación: La función de recursión (ecuación) parece tener una forma extraña. Cambiemos la variable T 2 (n) para obtener una ecuación de forma familiar; entonces, hacemos A(n) = T 3 (n); entonces tenemos:
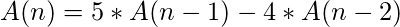
La ecuación característica de nuestra nueva ecuación diferencial sería:
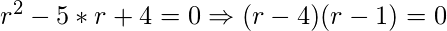
Entonces, la solución homogénea de esta ecuación será:
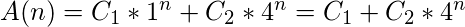
Como hemos definido A(n) = T 3 (n), la respuesta final es:
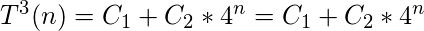
- Pregunta 2: ¡Determine el valor de la condición inicial F(1) de manera que podamos tener F(n) = (n+2)! como la solución a la siguiente función recursiva dada:
F(n) = (n+1) * F(n-1) + (n+1)!
- 3
- 4
- 6
- 2
Respuesta: 3
Explicación: Mediante el uso de la técnica de iteración para resolver la función recursiva dada, tendremos:
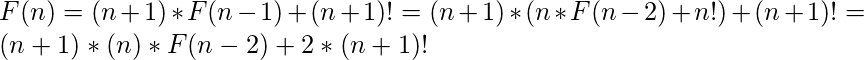
Si continuamos con estas derivaciones, podemos adivinar fácilmente que la respuesta debería ser de la siguiente forma:
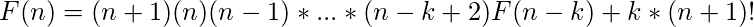
El último paso (punto de parada) en el método de iteración es cuando alcanzamos la condición inicial F(1); por lo tanto, hacemos k = n-1, y la forma no recursiva sería:

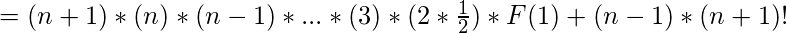
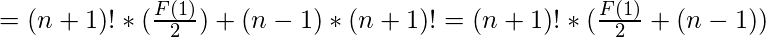
De acuerdo con la función dada F(n) en cuestión, y lo que hemos derivado hasta ahora:
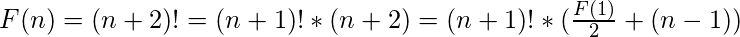
Finalmente, como veremos, el valor de F(1) es:
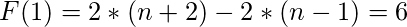
- Pregunta 3: ¿Cuál es la complejidad temporal de T(n) = 4* T(n/2) + n * log(n!).
- θ(n * registro n)
- θ(n 2 )
- θ(n 2 * log n)
- θ(n 2 * log 2 n)
Respuesta: 4
Explicación: Sabemos que log(n!) ∈ θ( norte * iniciar sesión norte ) .
Ahora, el problema equivalente es analizar el orden de la nueva función recursiva:
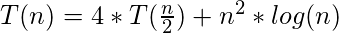
Podemos resolver esto por el teorema maestro . Para aplicar aquí el teorema maestro, tenemos f(n) = n 2 * log(n) , y los parámetros a (el número de subproblemas), b (el factor de reducción) y C igual a 4, 2 , y 2, respectivamente; entonces, θ( n log b a ), es de θ( n 2 ) que se encuentra en la misma clase de complejidad de θ( n C = 2 ); por lo tanto, la función recursiva dada pertenece al caso 2 del teorema maestro.
De acuerdo con el teorema del maestro, T(n) sería del siguiente orden:
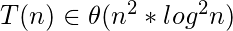
- Pregunta 4: ¿Cuál da la mejor estimación de la complejidad de T(n)?
T (n) =
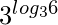 * T(n/2)+ n2 √.
* T(n/2)+ n2 √.- θ( n 2 * √ * log n )
- O( n 2 * √ * log n )
- θ(
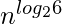 )
) - θ(
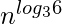 )
) - O( n 2 * √ ).
Respuesta: 3
Explicación: Sabemos que
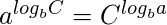 , y
, y 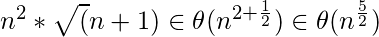 ; entonces, podemos simplificar la función de recursión de la siguiente manera:
; entonces, podemos simplificar la función de recursión de la siguiente manera: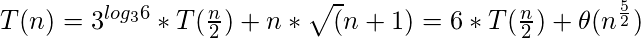
Pertenece al caso 3 del teorema maestro ; entonces, la complejidad asintótica de T(n) es:
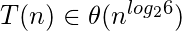
- Pregunta 5: ¿Qué límite asintótico no es correcto para T (n) = T (n/4) + T (3n/4) + n?
- O( n log 4/3 2 )
- Ω( n )
- O( n * log(n) )
- Ninguna de las anteriores
Respuesta: 4
Explicación: Por el teorema maestro , podemos especificar los mismos límites que se indican en las dos primeras opciones (A) y (B):
Podemos averiguar la corrección de la tercera opción mediante el método del árbol de recurrencia . Dibujamos un árbol y podemos adivinar fácilmente un límite apropiado para T(n) :

La longitud de las ramas del árbol de recurrencia no puede ser inferior a h r , ni tampoco puede ser superior a h L ; por lo que se pueden inferir las siguientes estimaciones:
De acuerdo con los dos límites mencionados anteriormente, también tenemos T(n) ∈ θ( n*log(n) ) .
Sabemos que si T(n) ∈ O(n * log(n)) , debe ser también de O(n log 4/3 n ) ; por lo tanto, si evaluamos primero la tercera opción, en realidad también habríamos inferido la corrección de la opción (A). Sin embargo, los árboles de recurrencia solo dan una idea de cómo adivinar un límite apropiado. Como alguien puede dar una suposición equivocada, este método también necesita verificación o prueba de que no violará la definición de las notaciones en uso. Esta verificación (prueba) puede obtenerse inductivamente mediante sustituciones iterativas en T(n), considerando las definiciones de la notación.