Búsqueda primero en amplitud sin utilizar la cola

La búsqueda en amplitud es un algoritmo de recorrido de gráfico que atraviesa un gráfico o un árbol nivel por nivel. En este artículo, BFS para un gráfico se implementa mediante la lista de adyacencia sin utilizar una cola .
Ejemplos: 

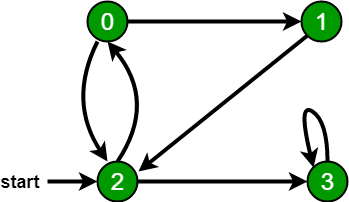
Aporte: 

Salida: recorrido BFS = 2, 0, 3, 1 
Explicación: 
en el siguiente gráfico, comenzamos el recorrido desde el vértice 2. Cuando llegamos al vértice 0, buscamos todos los vértices adyacentes. 2 también es un vértice adyacente de 0. Si no marcamos los vértices visitados, entonces 2 se procesará nuevamente y se convertirá en un proceso sin terminación. Por lo tanto, un recorrido primero en amplitud del siguiente gráfico es 2, 0, 3, 1. 
 

Enfoque: Este problema se puede resolver utilizando un simple recorrido transversal desde una fuente dada. La implementación utiliza la representación de listas de adyacencia de gráficos . 
Aquí: 
 

• El contenedor STL Vector se usa para almacenar listas de Nodes adyacentes y la cola de Nodes necesarios para el recorrido de BFS. 
   
• Se utiliza una array DP para almacenar la distancia de los Nodes desde la fuente. Cada vez que nos movemos de un Node a otro, la distancia aumenta en 1. Si la distancia para llegar a los Nodes se vuelve menor que la distancia anterior, actualizamos el valor almacenado en el DP[Node].

A continuación se muestra la implementación del enfoque anterior:

// C++ implementation to demonstrate
// the above mentioned approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the distance
// from the source to other nodes
void BFS(int curr, int N, vector<bool>& vis,
         vector<int>& dp, vector<int>& v,
         vector<vector<int> >& adj)
{
 
    while (curr <= N) {
 
        // Current node
        int node = v[curr - 1];
        cout << node << ", ";
 
        for (int i = 0; i < adj[node].size(); i++) {
 
            // Adjacent node
            int next = adj[node][i];
 
            if ((!vis[next])
                && (dp[next] < dp[node] + 1)) {
 
                // Stores the adjacent node
                v.push_back(next);
 
                // Increases the distance
                dp[next] = dp[node] + 1;
 
                // Mark it as visited
                vis[next] = true;
            }
        }
        curr += 1;
    }
}
 
// Function to print the distance
// from source to other nodes
void bfsTraversal(
    vector<vector<int> >& adj,
    int N, int source)
{
    // Initially mark all nodes as false
    vector<bool> vis(N + 1, false);
 
    // Initialize distance array with 0
    vector<int> dp(N + 1, 0), v;
 
    v.push_back(source);
 
    // Initially mark the starting
    // source as 0 and visited as true
    dp = 0;
    vis = true;
 
    // Call the BFS function
    BFS(1, N, vis, dp, v, adj);
}
 
// Driver code
int main()
{
    // No. of nodes in graph
    int N = 4;
 
    // Creating adjacency list
    // for representing graph
    vector<vector<int> > adj(N + 1);
    adj[0].push_back(1);
    adj[0].push_back(2);
    adj[1].push_back(2);
    adj[2].push_back(0);
    adj[2].push_back(3);
    adj[3].push_back(3);
 
    // Following is BFS Traversal
    // starting from vertex 2
    bfsTraversal(adj, N, 2);
 
    return 0;
}

# C++ implementation to demonstrate
# the above mentioned approach
from queue import Queue
 
# Function to find the distance
# from the source to other nodes
def BFS(curr, N, vis,          dp,  v, adj):
 
    while (curr <= N) :
 
        # Current node
        node = v[curr - 1]
        print(node,end=  ", ")
 
        for i in range(len(adj[node])) :
 
            # Adjacent node
            next = adj[node][i]
 
            if ((not vis[next]) and (dp[next] < dp[node] + 1)) :
 
                # Stores the adjacent node
                v.append(next)
 
                # Increases the distance
                dp[next] = dp[node] + 1
 
                # Mark it as visited
                vis[next] = True
             
         
        curr += 1
     
 
 
# Function to print the distance
# from source to other nodes
def bfsTraversal(adj,    N, source):
    # Initially mark all nodes as false
    vis=[False]*(N + 1)
 
    # Initialize distance array with 0
    dp=[0]*(N + 1); v=[]
 
    v.append(source)
 
    # Initially mark the starting
    # source as 0 and visited as true
    dp = 0
    vis = True
 
    # Call the BFS function
    BFS(1, N, vis, dp, v, adj)
 
 
# Driver code
if __name__ == '__main__':
    # No. of nodes in graph
    N = 4
 
    # Creating adjacency list
    # for representing graph
    adj=[[] for _ in range(N+1)]
    adj[0].append(1)
    adj[0].append(2)
    adj[1].append(2)
    adj[2].append(0)
    adj[2].append(3)
    adj[3].append(3)
 
    # Following is BFS Traversal
    # starting from vertex 2
    bfsTraversal(adj, N, 2)

2, 0, 3, 1, 

Complejidad temporal: O(V + E), donde V es el número de vértices y E es el número de aristas.
Espacio Auxiliar: O(V)