Análisis de datos con SciPy

Posted on by Rudeus Greyrat

SciPy es una biblioteca de Python que es útil para resolver muchas ecuaciones y algoritmos matemáticos. Está diseñado en la parte superior de la biblioteca Numpy que brinda una mayor extensión para encontrar fórmulas matemáticas científicas como Matrix Rank, Inverse, ecuaciones polinómicas, descomposición LU, etc. El uso de sus funciones de alto nivel reducirá significativamente la complejidad del código y ayuda a analizar mejor los datos. SciPy es una sesión interactiva de Python que se utiliza como una biblioteca de procesamiento de datos que está diseñada para competir con sus rivales, como MATLAB, Octave, R-Lab, etc. Tiene muchas funciones fáciles de usar, eficientes y fáciles de usar que ayudan a resolver problemas como integración numérica, interpolación, optimización, álgebra lineal y estadísticas.

El beneficio de usar la biblioteca SciPy en Python mientras se crean modelos ML es que también pone a disposición un lenguaje de programación sólido para usar en el desarrollo de programas y aplicaciones menos complejos.

# import numpy library
import numpy as np
A = np.array([[1,2,3],[4,5,6],[7,8,8]])

Álgebra lineal

  1. Determinante de una array

    # importing linalg function from scipy
    from scipy import linalg
      
    # Compute the determinant of a matrix
    linalg.det(A)
    		 
    Output :
2.999999999999997
  2. Calcular la descomposición LU pivotada de una array
    La descomposición LU es un método que reduce la array en partes constituyentes que ayuda a calcular con mayor facilidad operaciones complejas con arrays. Los métodos de descomposición también se denominan métodos de factorización de arrays, son base del álgebra lineal en computadoras, incluso para operaciones básicas como resolver sistemas de ecuaciones lineales, calcular la inversa y calcular el determinante de una array.
    La descomposición es:
    A = PLU
    donde P es una array de permutación, L triangular inferior con elementos diagonales unitarios y U triangular superior.

    P, L, U = linalg.lu(A)
    print(P)
    print(L)
    print(U)
    # print LU decomposition
    print(np.dot(L,U))
    		 
    Output :
array([[ 0.,  1.,  0.],
       [ 0.,  0.,  1.],
       [ 1.,  0.,  0.]])

array([[ 1.        ,  0.        ,  0.        ],
       [ 0.14285714,  1.        ,  0.        ],
       [ 0.57142857,  0.5       ,  1.        ]])

array([[ 7.        ,  8.        ,  8.        ],
       [ 0.        ,  0.85714286,  1.85714286],
       [ 0.        ,  0.        ,  0.5       ]])

array([[ 7.,  8.,  8.],
       [ 1.,  2.,  3.],
       [ 4.,  5.,  6.]])
  3. Valores propios y vectores propios de esta array

    eigen_values, eigen_vectors = linalg.eig(A)
    print(eigen_values)
    print(eigen_vectors)
    		 
    Output :
array([ 15.55528261+0.j,  -1.41940876+0.j,  -0.13587385+0.j])

array([[-0.24043423, -0.67468642,  0.51853459],
       [-0.54694322, -0.23391616, -0.78895962],
       [-0.80190056,  0.70005819,  0.32964312]])
  4. También se pueden resolver sistemas de ecuaciones lineales

    v = np.array([[2],[3],[5]])
    print(v)
    s = linalg.solve(A,v)
    print(s)
    		 
    Output :
array([[2],
       [3],
       [5]])

array([[-2.33333333],
       [ 3.66666667],
       [-1.        ]])

Álgebra lineal dispersa

SciPy tiene algunas rutinas para computar con arrays dispersas y potencialmente muy grandes. Las herramientas necesarias están en el submódulo scipy.sparse.
Veamos cómo construir una array dispersa grande:

# import necessary modules
from scipy import sparse
# Row-based linked list sparse matrix
A = sparse.lil_matrix((1000, 1000))
print(A)
  
A[0,:100] = np.random.rand(100)
A[1,100:200] = A[0,:100]
A.setdiag(np.random.rand(1000))
print(A)

Output :
<1000x1000 sparse matrix of type ''
    with 0 stored elements in LInked List format>

<1000x1000 sparse matrix of type ''
    with 1199 stored elements in LInked List format>
  1. Álgebra lineal para arrays dispersas

    from scipy.sparse import linalg
      
    # Convert this matrix to Compressed Sparse Row format.
    A.tocsr()
      
    A = A.tocsr()
    b = np.random.rand(1000)
    ans = linalg.spsolve(A, b)
    # it will print ans array of 1000 size
    print(ans)
    		 
    Output :
array([-2.53380006e+03, -1.25513773e+03,  9.14885544e-01,  2.74521543e+00,
        5.99942835e-01,  4.57778093e-01,  1.87104209e-01,  2.15228367e+00,
        8.78588432e-01,  1.85105721e+03,  1.00842538e+00,  4.33970632e+00,
        5.26601699e+00,  2.17572231e-01,  1.79869079e+00,  3.83800946e-01,
        2.57817130e-01,  5.18025462e-01,  1.68672669e+00,  3.07971950e+00,
        6.20604437e-01,  1.41365890e-01,  3.18167429e-01,  2.06457302e-01,
        8.94813817e-01,  5.06084834e+00,  5.00913942e-01,  1.37391305e+00,
        2.32081425e+00,  4.98093749e+00,  1.75492222e+00,  3.17278127e-01,
        8.50013844e-01,  1.17524493e+00,  1.70173722e+00,  .............))

Integración

Cuando una función es muy difícil de integrar analíticamente, uno simplemente encuentra una solución a través de métodos de integración numérica. SciPy también tiene la capacidad de realizar integración numérica. Scipy tiene métodos de integración en el módulo scipy.integrate .

  1. Integrales simples
    La rutina Quad es la función importante de las funciones de integración de SciPy. Si la integración en la función f(x) donde x varía de a a b, entonces la integral se ve así.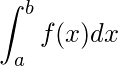
    \displaystyle\int_{a}^{b} f(x) dx
    Los parámetros de quad son scipy.integrate.quad(f, a, b), donde ‘f’ es la función a integrar. Mientras que ‘a’ y ‘b’ son los rangos inferior y superior del límite x. Veamos un ejemplo de integración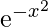 $e^{-x^2}$en el rango de 0 y 1 con respecto a dx .
    Primero definiremos la función f(x)=e^(-x^2), esto se hace usando una expresión lambda y luego usamos la rutina cuádruple.

    import scipy.integrate
    f= lambda x:np.exp(-x**2)
    # print results
    i = scipy.integrate.quad(f, 0, 1)
    print(i)
    		 
    (0.7468241328124271, 8.291413475940725e-15)

    La función cuádruple devuelve los dos valores, en los que el primer número es el valor de la integral y el segundo valor es el error probable en el valor de la integral.

  2. Integrales dobles
    Los parámetros de la función dblquad son scipy.integrate.dblquad(f, a, b, g, h) . Donde, ‘f’ es la función a integrar, ‘a’ y ‘b’ son los rangos inferior y superior de la variable x, respectivamente, mientras que ‘g’ y ‘h’ son las funciones que indican los límites inferior y superior de y variable.
    Como ejemplo, realicemos la integral doble de x*y^2 sobre el rango de x de 0 a 2 y el rango de y de 0 a 1.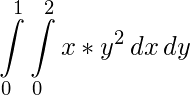
    \newcommand{\Int}{\int\limits} \displaystyle \Int_{0}^{1} \Int_{0}^{2} x*y^2 \,dx\,dy
    Definimos las funciones f, g y h usando las expresiones lambda. Tenga en cuenta que incluso si g y h son constantes, como pueden serlo en muchos casos, deben definirse como funciones, como lo hemos hecho aquí para el límite inferior.

    from scipy import integrate
    f = lambda y, x: x*y**2
    i = integrate.dblquad(f, 0, 2, lambda x: 0, lambda x: 1)
    # print the results
    print(i)
    		 
    Output :
 (0.6666666666666667, 7.401486830834377e-15)

Hay mucho más de lo que SciPy es capaz, como transformadas de Fourier, funciones de Bessel, etc.
¡Puede consultar la documentación para obtener más detalles!

Publicación traducida automáticamente

Artículo escrito por tyagikartik4282 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *