Análisis del valor de frontera: problema del triángulo

El análisis de valor límite (BVA) es una técnica de prueba de software de caja negra en la que los casos de prueba se diseñan utilizando valores límite. BVA se basa en la suposición de falla única , también conocida como suposición de falla crítica, que establece que las fallas rara vez son el producto de dos o más fallas simultáneas. Por lo tanto, mientras diseñamos los casos de prueba para BVA, mantenemos todas las variables menos una en el valor nominal y permitimos que la variable restante tome el valor extremo. 

Diseño de casos de prueba para BVA: 
Mientras diseñamos los casos de prueba para BVA, primero determinamos el número de variables de entrada en el problema. Para cada variable de entrada, determinamos el rango de valores que puede tomar. Luego determinamos los valores extremos y el valor nominal para cada variable de entrada. 

Considere una variable de entrada t que toma valores en el rango [l, r]. Los valores extremos para t son: 
 

t = l
t = l+1
t = r-1
t = r 

El valor nominal de la variable puede ser cualquier valor en el rango (l, r). 
En la mayoría de las implementaciones de BVA, se toma como el valor medio del rango (r+l)/2. 
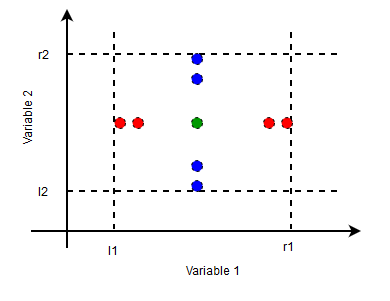
La figura de la derecha muestra los valores nominales y extremos para el valor límite del análisis de un problema de dos variables. 

Bajo el supuesto de falla única, el número total de casos de prueba en BVA para un problema con n entradas es 4n+1. 
Los 4n casos corresponden a los casos de prueba con los cuatro valores extremos de cada variable manteniendo la otra n-1 variable en valor nominal. El único caso adicional es cuando todas las variables se mantienen en un valor nominal. 

Uno de los problemas comunes para el diseño de casos de prueba utilizando BVA es el problema del triángulo que se analiza a continuación: 

Triangle Problem acepta tres números enteros: a, b, c como tres lados del triángulo. También definimos un rango para los lados del triángulo como [l, r] donde l>0. Devuelve el tipo de triángulo (Escaleno, Isósceles, Equilátero, No Triángulo) formado por a, b, c. 

Para que a, b, c formen un triángulo, se deben cumplir las siguientes condiciones: 

a < b+c
b < a+c
c < a+b 

Si se viola alguna de estas condiciones, el resultado es No es un triángulo.  

• Para Triángulo Equilátero todos los lados son iguales.
• Para el Triángulo Isósceles exactamente un par de lados es igual.
• Para el Triángulo Escaleno todos los lados son diferentes.

La tabla muestra el diseño de casos de prueba para el problema del triángulo. El valor del rango [l, r] se toma como [1, 100] y el valor nominal se toma como 50. 

El total de casos de prueba es,  

4n+1 = 4*3+1 = 13 

ID de caso de prueba	a	b	C	Rendimiento esperado
T1	1	50	50	Isósceles
T2	2	50	50	Isósceles
T3	99	50	50	Isósceles
T4	100	50	50	no es un triangulo
T5	50	50	50	Equilátero
T6	50	1	50	Isósceles
T7	50	2	50	Isósceles
T8	50	99	50	Isósceles
T9	50	100	50	no es un triangulo
T10	50	50	1	Isósceles
T11	50	50	2	Isósceles
T12	50	50	99	Isósceles
T13	50	50	100	no es un triangulo