Análisis Discriminante Regularizado
El análisis Discriminante Lineal y QDA funcionan directamente para los casos en los que un número de observaciones es mucho mayor que el número de predictores n>p. En estas situaciones, ofrece muchas ventajas como la facilidad de aplicación (ya que no tenemos que calcular la covarianza para cada clase) y la robustez a las desviaciones de los supuestos del modelo.
Sin embargo, el uso de LDA se convierte en un desafío serio cuando, por ejemplo, el número de observaciones es menor que los predictores, como la configuración de microarrays, porque aquí hay dos desafíos.
- La array de covarianza de la muestra es singular y no se puede invertir.
- La alta dimensionalidad hace que la operación matricial directa sea formidable, lo que dificulta la aplicabilidad de este método.
Por lo tanto, haremos algunos cambios en LDA y QDA, es decir, formaremos una nueva array de covarianza que combina la array de covarianza de LDA ( ![]() ) y QDA (
) y QDA ( ![]() ) usando un parámetro de ajuste
) usando un parámetro de ajuste ![]()
![]()
Sin embargo, alguna versión del análisis discriminante regularizado usa otro parámetro ( ![]() ) con la siguiente ecuación:
) con la siguiente ecuación:
![]()
RDA limita la covarianza separada de QDA hacia la covarianza común de LDA. Esto mejora las estimaciones de la array de covarianza en situaciones en las que el número de predictores es mayor que el número de muestras en los datos de entrenamiento, lo que conduce a una mejora en la precisión del modelo.
En la ecuación anterior, la ecuación \gamma y \lambda ambas tienen valores b/w 0 y 1. Ahora, para los cuatro valores límite, produce un caso de ecuación especial para cada uno. Veamos estos casos especiales:
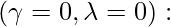 la covarianza de QDA, es decir, la covarianza individual de cada grupo.
la covarianza de QDA, es decir, la covarianza individual de cada grupo.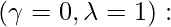 la covarianza de LDA, es decir, una array de covarianza común.
la covarianza de LDA, es decir, una array de covarianza común.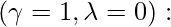 varianza independiente condicional.
varianza independiente condicional.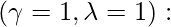 la
la
Implementación
- En esta implementación, realizaremos un análisis discriminante regularizado. Usaremos la biblioteca klaR y la función rda en ella. También utilizamos el conjunto de datos del iris.
R
# imports
library(tidyverse)
library(MASS)
library(klaR)
data('iris')
# model
# divide the data into train and test
train_test.samples <- iris$Species %>% createDataPartition(p = 0.8, list = FALSE)
train.data <- iris[train_test.samples, ]
test.data <- iris[-train_test.samples, ]
# Data preprocessing
# Normalize the different parameters of dataset and categorical
# variables also includes
preproc.param <- train.data %>%
preProcess(method = c("center", "scale"))
# Transform the data using the estimated parameters
train.transformed <- preproc.param %>% predict(train.data)
test.transformed <- preproc.param %>% predict(test.data)
# define rda models
model = rda(Species ~. , data= train.transformed)
model
# run the model on test data and generate the prediction
predictions <- model %>% predict(test.transformed)
# calculate model accuracy
mean(predictions$class==test.transformed$Species)
Producción:
Call:
rda(formula = Species ~ ., data = train.transformed)
Regularization parameters:
gamma lambda
0.002619109 0.222244278
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Misclassification rate:
apparent: 1.667 %
cross-validated: 1.667 %
### accuracy
0.9666667