Ángulo entre un par de líneas en 3D

Posted on by Rudeus Greyrat

Dadas las coordenadas de tres puntos A(x1, y1, z1), B(x2, y2, z2) y C(x3, y3, z3) en un plano 3D, donde B es el punto de intersección de la línea AB y BC , el tarea es encontrar el ángulo entre las líneas AB y BC .
 

Ejemplos: 
 

Entrada: x1 = 1, y1 = 3, z1 = 3; x2 = 3, y2 = 4, z2 = 5; x3 = 5, y3 = 6, z3 = 9; 
Salida: 54,6065
Entrada: x1 = 10, y1 = 10, z1 = 10; x2 = 0, y2 = 0, z2 = 0; x3 = 15, y3 = 10, z3 = 15; 
Salida: 56.4496  

Acercarse:
 

1. Encuentra la ecuación de las líneas AB y BC con las coordenadas dadas en términos de relaciones de dirección como: 
 

AB = (x1 – x2)i + (y1 – y2)j + (z1 – z2)k 
BC = (x3 – x2)i + (y3 – y2)j + (z3 – z2)k 
 

2. Usa la fórmula para cos Θ para las dos razones de dirección de las líneas AB y BC para encontrar el coseno del ángulo entre las líneas AB y BC como: 
 

donde, 
AB.BC es el producto escalar de las relaciones de dirección AB y BC. 
|AB| es la magnitud de la línea AB 
|BC| es la magnitud de la línea BC 

3. Supongamos que hay dos razones de dirección: 
 

A = ai + bj + ck
B = xi + yj + zk

 después 

Producto punto (AB) = a*x + b*y + c*z 
magnitud de A = |A| =  \sqrt{a^{2} + b^{2} + c^{2}}
magnitud de B = |B| =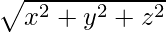 \sqrt{x^{2} + y^{2} + z^{2}}  

4. El coseno del ángulo calculado da el valor del coseno en radianes. Para encontrar el ángulo, multiplique el valor del coseno por (180/ Π ) .

A continuación se muestra la implementación del enfoque anterior:
 

C++

// C++ program for the above approach
 
#include "bits/stdc++.h"
#define PI 3.14
using namespace std;
 
// Function to find the angle between
// the two lines
void calculateAngle(
    int x1, int y1, int z1,
    int x2, int y2, int z2,
    int x3, int y3, int z3)
{
    // Find direction ratio of line AB
    int ABx = x1 - x2;
    int ABy = y1 - y2;
    int ABz = z1 - z2;
 
    // Find direction ratio of line BC
    int BCx = x3 - x2;
    int BCy = y3 - y2;
    int BCz = z3 - z2;
 
    // Find the dotProduct
    // of lines AB & BC
    double dotProduct
        = ABx * BCx
          + ABy * BCy
          + ABz * BCz;
 
    // Find magnitude of
    // line AB and BC
    double magnitudeAB
        = ABx * ABx
          + ABy * ABy
          + ABz * ABz;
    double magnitudeBC
        = BCx * BCx
          + BCy * BCy
          + BCz * BCz;
 
    // Find the cosine of
    // the angle formed
    // by line AB and BC
    double angle = dotProduct;
    angle /= sqrt(
        magnitudeAB * magnitudeBC);
 
    // Find angle in radian
    angle = (angle * 180) / PI;
 
    // Print the angle
    cout << abs(angle) << endl;
}
 
// Driver Code
int main()
{
 
    // Given coordinates
    // Points A
    int x1 = 1, y1 = 3, z1 = 3;
 
    // Points B
    int x2 = 3, y2 = 4, z2 = 5;
 
    // Points C
    int x3 = 5, y3 = 6, z3 = 9;
 
    // Function Call
    calculateAngle(x1, y1, z1,
                   x2, y2, z2,
                   x3, y3, z3);
 
    return 0;
}

Java

// Java program for the above approach
import java.util.*;
 
class GFG{
     
// Function to find the angle
// between the two lines
static void calculateAngle(int x1, int y1, int z1,
                           int x2, int y2, int z2,
                           int x3, int y3, int z3)
{
     
    // Find direction ratio of line AB
    int ABx = x1 - x2;
    int ABy = y1 - y2;
    int ABz = z1 - z2;
 
    // Find direction ratio of line BC
    int BCx = x3 - x2;
    int BCy = y3 - y2;
    int BCz = z3 - z2;
 
    // Find the dotProduct
    // of lines AB & BC
    double dotProduct = ABx * BCx +
                        ABy * BCy +
                        ABz * BCz;
 
    // Find magnitude of
    // line AB and BC
    double magnitudeAB = ABx * ABx +
                         ABy * ABy +
                         ABz * ABz;
    double magnitudeBC = BCx * BCx +
                         BCy * BCy +
                         BCz * BCz;
 
    // Find the cosine of the
    // angle formed by line
    // AB and BC
    double angle = dotProduct;
    angle /= Math.sqrt(magnitudeAB * magnitudeBC);
 
    // Find angle in radian
    angle = (angle * 180) / 3.14;
 
    // Print the angle
    System.out.printf("%.4f", Math.abs(angle));
}
 
// Driver code
public static void main(String[] args)
{
 
    // Given coordinates
    // Points A
    int x1 = 1, y1 = 3, z1 = 3;
 
    // Points B
    int x2 = 3, y2 = 4, z2 = 5;
 
    // Points C
    int x3 = 5, y3 = 6, z3 = 9;
 
    // Function Call
    calculateAngle(x1, y1, z1,
                   x2, y2, z2,
                   x3, y3, z3);
}
}
 
// This code is contributed by offbeat

Python3

# Python3 program for the above approach
import math
 
# Function to find the angle
# between the two lines
def calculateAngle(x1, y1, z1,
                   x2, y2, z2,
                   x3, y3, z3):
                        
    # Find direction ratio of line AB
    ABx = x1 - x2;
    ABy = y1 - y2;
    ABz = z1 - z2;
 
    # Find direction ratio of line BC
    BCx = x3 - x2;
    BCy = y3 - y2;
    BCz = z3 - z2;
 
    # Find the dotProduct
    # of lines AB & BC
    dotProduct = (ABx * BCx +
                  ABy * BCy +
                  ABz * BCz);
 
    # Find magnitude of
    # line AB and BC
    magnitudeAB = (ABx * ABx +
                   ABy * ABy +
                   ABz * ABz);
    magnitudeBC = (BCx * BCx +
                   BCy * BCy +
                   BCz * BCz);
 
    # Find the cosine of
    # the angle formed
    # by line AB and BC
    angle = dotProduct;
    angle /= math.sqrt(magnitudeAB *
                       magnitudeBC);
 
    # Find angle in radian
    angle = (angle * 180) / 3.14;
 
    # Print angle
    print(round(abs(angle), 4))
 
# Driver Code
if __name__=='__main__':
 
    # Given coordinates
    # Points A
    x1, y1, z1 = 1, 3, 3;
 
    # Points B
    x2, y2, z2 = 3, 4, 5;
 
    # Points C
    x3, y3, z3 = 5, 6, 9;
  
    # Function Call
    calculateAngle(x1, y1, z1,
                   x2, y2, z2,
                   x3, y3, z3);
 
# This code is contributed by AbhiThakur

C#

// C# program for the above approach
using System;
class GFG{
     
// Function to find the angle
// between the two lines
static void calculateAngle(int x1, int y1,
                           int z1, int x2,
                           int y2, int z2,
                           int x3, int y3,
                           int z3)
{
     
    // Find direction ratio of line AB
    int ABx = x1 - x2;
    int ABy = y1 - y2;
    int ABz = z1 - z2;
 
    // Find direction ratio of line BC
    int BCx = x3 - x2;
    int BCy = y3 - y2;
    int BCz = z3 - z2;
 
    // Find the dotProduct
    // of lines AB & BC
    double dotProduct = ABx * BCx +
                        ABy * BCy +
                        ABz * BCz;
 
    // Find magnitude of
    // line AB and BC
    double magnitudeAB = ABx * ABx +
                         ABy * ABy +
                         ABz * ABz;
    double magnitudeBC = BCx * BCx +
                         BCy * BCy +
                         BCz * BCz;
 
    // Find the cosine of the
    // angle formed by line
    // AB and BC
    double angle = dotProduct;
    angle /= Math.Sqrt(magnitudeAB *
                       magnitudeBC);
 
    // Find angle in radian
    angle = (angle * 180) / 3.14;
 
    // Print the angle
    Console.Write(String.Format("{0:F4}", Math.Abs(angle)));
}
 
// Driver code
public static void Main()
{
 
    // Given coordinates
    // Points A
    int x1 = 1, y1 = 3, z1 = 3;
 
    // Points B
    int x2 = 3, y2 = 4, z2 = 5;
 
    // Points C
    int x3 = 5, y3 = 6, z3 = 9;
 
    // Function Call
    calculateAngle(x1, y1, z1,
                   x2, y2, z2,
                   x3, y3, z3);
}
}
 
// This code is contributed by Code_Mech

Javascript

<script>
 
 
// Javascript program for the above approach
 
var PI = 3.14;
 
// Function to find the angle between
// the two lines
function calculateAngle(
    x1, y1, z1,
    x2, y2, z2,
    x3, y3, z3)
{
    // Find direction ratio of line AB
    var ABx = x1 - x2;
    var ABy = y1 - y2;
    var ABz = z1 - z2;
 
    // Find direction ratio of line BC
    var BCx = x3 - x2;
    var BCy = y3 - y2;
    var BCz = z3 - z2;
 
    // Find the dotProduct
    // of lines AB & BC
    var dotProduct
        = ABx * BCx
          + ABy * BCy
          + ABz * BCz;
 
    // Find magnitude of
    // line AB and BC
    var magnitudeAB
        = ABx * ABx
          + ABy * ABy
          + ABz * ABz;
    var magnitudeBC
        = BCx * BCx
          + BCy * BCy
          + BCz * BCz;
 
    // Find the cosine of
    // the angle formed
    // by line AB and BC
    var angle = dotProduct;
    angle /= Math.sqrt(
        magnitudeAB * magnitudeBC);
 
    // Find angle in radian
    angle = (angle * 180) / PI;
 
    // Print the angle
    document.write(Math.abs(angle).toFixed(4));
}
 
// Driver Code
// Given coordinates
// Points A
var x1 = 1, y1 = 3, z1 = 3;
// Points B
var x2 = 3, y2 = 4, z2 = 5;
// Points C
var x3 = 5, y3 = 6, z3 = 9;
// Function Call
calculateAngle(x1, y1, z1,
               x2, y2, z2,
               x3, y3, z3);
 
 
</script>
Producción: 

54.6065

 

Publicación traducida automáticamente

Artículo escrito por Yogesh Shukla 1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *