Las líneas rectas en el espacio 3D generalmente se representan en dos formas: forma cartesiana y forma vectorial . Por lo tanto, los ángulos entre dos líneas rectas cualesquiera en el espacio 3D también se definen en términos de ambas formas de las líneas rectas. Analicemos los métodos para encontrar el ángulo entre dos líneas rectas en ambas formas, una por una.
Forma cartesiana
L 1 : (x – x 1 ) / a 1 = (y – y 1 ) / b 1 = (z – z 1 ) / c 1
L 2 : (x – x 2 ) / a 2 = (y – y 2 ) / b 2 = (z – z 2 ) / c 2
Aquí L 1 y L 2 representan las dos líneas rectas que pasan por los puntos (x 1 , y 1 , z 1 ) y (x 2 , y 2 , z 2 ) respectivamente en el espacio 3D en forma cartesiana.
- Las razones de dirección de la línea L 1 son a 1 , b 1 , c 1 luego un vector paralelo a L 1 es
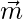 1 = a 1 i + b 1 j + c 1 k
1 = a 1 i + b 1 j + c 1 k - Las relaciones de dirección de la línea L 2 son a 2 , b 2 , c 2 luego un vector paralelo a L 2 es
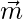 2 = a 2 i + b 2 j + c 2 k
2 = a 2 i + b 2 j + c 2 k
Entonces el ángulo ∅ entre L 1 y L 2 viene dado por:
∅ = cos -1 {(
1 .
2 ) / (|
1 | × |
2 |)}
Ejemplos
Ejemplo 1: (x – 1) / 1 = (2y + 3) / 3 = (z + 5) / 2 y (x – 2) / 3 = (y + 1) / -2 = (z – 2) / 0 son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
Solución:
1 = 1 yo + (3 / 2) j + 2 k
2 = 3 yo – 2 j + 0 k
|
1 | = √(1 2 + (3/2) 2 + 2 2 ) = √(29 / 2)
|
2 | = √(3 2 + 2 2 + 0 2 ) = √(13)
∅ = cos -1 {(1×3 + (3/2)×(-2) + (2)×0 ) / ((√(29) / 2) × √(13))}
∅ = cos -1 {0 / ((√(29) / 2) × √(13))}
∅ = cos -1 (0)
∅ = π / 2
Ejemplo 2: encuentre los ángulos entre las dos líneas en el espacio 3D cuyas únicas proporciones de dirección son 2, 1, 2 y 2, 3, 1. En la pregunta, no se dan las ecuaciones de las 2 líneas, solo se dan sus DR. Entonces el ángulo ∅ entre las 2 rectas viene dado por:
Solución:
1 = Vector paralelo a la línea que tiene DRs 2, 1, 2 = (2 i + j + 2 k )
|
1 | = √(2 2 + 1 2 + 2 2 ) = √9 = 3
2 = Vector paralelo a la línea que tiene DRs 2, 3, 1 = (2 i + 3 j + k )
|
2 | = √(2 2 + 3 2 + 1 2 ) = √(14)
∅ = cos -1 {(2×2 + 1×3 + 2×1) / (3 × √(14))}
∅ = cos -1 {(4 + 3 + 2) / (3 × √(14))}
∅ = cos -1 {9 / (3 × √(14))}
∅ = cos -1 (3 / √(14))
Ejemplo 3: (x – 1) / 2 = (y – 2) / 1 = (z – 3) / 2 y (x – 2) / 2 = (y – 1) / 2 = (z – 3) / 1 son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
Solución:
1 = 2 yo + j + 2 k
|
1 | = √(2 2 + 1 2 + 2 2 ) = √9 = 3
2 = 2 yo + 2 j + k
|
2 | = √(2 2 + 2 2 + 1 2 ) = √9 = 3
∅ = cos -1 {(2×2 + 1×2 + 2×1 ) / (3 × 3)}
∅ = cos -1 {(4 + 2 + 2) / 9}
∅ = cos -1 (8 / 9)
Forma vectorial
L 1 : ![]() =
= ![]() 1 + t .
1 + t . ![]() 1
1
L 2 : ![]() =
= ![]() 2 + tu .
2 + tu . ![]() 2
2
Aquí L 1 y L 2 representan las dos líneas rectas que pasan por los puntos cuyos vectores de posición son 1 y 2 respectivamente en el espacio 3D en forma vectorial. 1 y 2 son los dos vectores paralelos a L 1 y L 2 respectivamente y t y u son los parámetros. Entonces el ángulo ∅ entre los vectores 1 y 2 es igual al ángulo entre L 1 y L 2 viene dado por: ![]()
![]()
![]()
![]()
![]()
![]()
∅ = cos -1 {(
1 .
2 ) / (|
1 | × |
2 |)}
Ejemplos
Ejemplo 1: ![]() = (i + j + k) + t × {(-√3 – 1) i + (√3 – 1) j + 4 k} y
= (i + j + k) + t × {(-√3 – 1) i + (√3 – 1) j + 4 k} y ![]() = (i + j + k) + u × (i + j + 2 k) son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
= (i + j + k) + u × (i + j + 2 k) son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
Solución:
1 = (-√3 – 1) yo + (√3 – 1) j + 4k
|
1 | = √{(-√3 – 1) 2 + (√3 – 1) 2 + 4 2 )} = √(24)
2 = yo + j + 2k
|
2 | = √(1 2 + 1 2 + 2 2 ) = √6
∅ = cos -1 {(-√3 – 1)×1 + (√3 – 1)×1 + 4×2 ) / (√(24) × √6)}
∅ = cos -1 {6 / (√(24) × √6)}
∅ = cos -1 (½)
∅ = π / 3
Ejemplo 2: (i + 2 j + 2 k) y (3 i + 2 j + 6 k) son los dos vectores paralelos a las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellos está dado por:
Solución:
1 = yo + 2j + 2k
|
1 | = √(1 2 + 2 2 + 2 2 )} = √9 = 3
2 = 3 yo + 2 j + 6 k
|
2 | = √(3 2 + 2 2 + 6 2 ) = √(49) = 7
∅ = cos -1 {(1×3 + 2×2 + 2×6) / (7 × 3)}
∅ = cos -1 {(3 + 4 + 12) / 21}
∅ = cos -1 (19 / 21)
Ejemplo 3: ![]() = (3 i + 5 j + 7 k) + s × {(i + 2 j – 2 k} y
= (3 i + 5 j + 7 k) + s × {(i + 2 j – 2 k} y ![]() = (4 i + 3 j + k) + t × (2 i + 4 j – 4 k ) son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
= (4 i + 3 j + k) + t × (2 i + 4 j – 4 k ) son las dos líneas en el espacio 3D, entonces el ángulo ∅ entre ellas viene dado por:
Solución:
1 = yo + 2 j – 2 k
|
1 | = √(1 2 + 2 2 + (-2) 2 )} = √9 = 3
2 = 2 yo + 4 j – 4 k
|
2 | = √(2 2 + 4 2 + (-4) 2 ) = √(36) = 6
∅ = cos -1 {(1×2 + 2×4 + (-2)×(-4)) / (3 × 6)}
∅ = cos -1 {(2 + 8 + 8) / 18}
∅ = cos -1 (18 / 18)
∅ = cos -1 (1) = 0