Requisito previo: ANN | Red neuronal autoorganizada (SONN)
En la red neuronal autoorganizada (SONN), el aprendizaje se realiza cambiando los pesos de las conexiones inactivas a las activas. Las neuronas que se ganaron se seleccionan para aprender junto con sus neuronas vecinas. Si una neurona no responde a un patrón de entrada específico, entonces el aprendizaje no se realizará en esa neurona en particular.
Algoritmo de aprendizaje de red neuronal autoorganizado:
Paso 0:
- Inicialice los pesos sinápticos
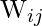 a valores aleatorios en un intervalo específico como [-1, 1] o [0, 1].
a valores aleatorios en un intervalo específico como [-1, 1] o [0, 1]. - Asigne parámetros topológicos de vecindad.
- Defina la tasa de aprendizaje
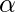 (por ejemplo, 0,1).
(por ejemplo, 0,1).
Paso 1: Hasta que se alcance la condición de terminación, hacer un ciclo: Pasos 2-8
![Rendered by QuickLaTeX.com \[$D(j) = \left\|\mathbf{X}-\mathbf{W}_{j}\right\|=\left[\sum_{i=1}^{n}\left(x_{i}-w_{i j}\right)^{2}\right]^{1 / 2}$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5353339f6bb7ba4ae8dce38720e91306_l3.png)
Este es un criterio para encontrar similitud entre dos conjuntos de muestras. Se evalúan los Nodes (neuronas) de la red para determinar el vector de entrada más probable según sus pesos
![Rendered by QuickLaTeX.com \[$j_{\mathbf{X}}(p)=\min _{j}\left\|\mathbf{X}-\mathbf{W}_{j}(p)\right\|=\left\{\sum_{i=1}^{n}\left[x_{i}-w_{i j}(p)\right]^{2}\right\}^{1 / 2}$\\ $j = 1, 2, \ldots, m$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e2886bdb0d302d173c057d298aa7265_l3.png)
Donde: ![]() es el número de neuronas en la capa de entrada,
es el número de neuronas en la capa de entrada, ![]() es el número de neuronas en la capa de Kohonen.
es el número de neuronas en la capa de Kohonen.
El Node ganador generalmente se denomina como la mejor unidad de coincidencia (BMU).
![]()
¿Dónde ![]() está la corrección de peso en la iteración
está la corrección de peso en la iteración ![]() ?
?
Este proceso de actualización de peso se basa en la regla de aprendizaje competitivo:
![Rendered by QuickLaTeX.com \[$\Delta w_{i j}(p) = \left\{\begin{array}{cl}\alpha\left(x_{i}-w_{i j}(p)\right), & \text { if neuron } j \text { wins the competition } \\ 0, & \text { if neuron } j \text { loses the competition }\end{array}\right.$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bfaebc32cfb926180e389e30a56205ae_l3.png)
¿Dónde ![]() está la tasa de aprendizaje?
está la tasa de aprendizaje?
Aquí, la función de vecindad se centró en la neurona ganadora se lo lleva todo ![]() en la iteración
en la iteración ![]() . Cualquier neurona dentro del radio de la BMU se modifica para hacerla más similar al vector de entrada.
. Cualquier neurona dentro del radio de la BMU se modifica para hacerla más similar al vector de entrada.
![]()
Ejemplo con iteraciones:
Tome un vector de entrada de 2 – Dimensión:![Rendered by QuickLaTeX.com $\mathbf{X}=\left[\begin{array}{l}0.52 \\ 0.12\end{array}\right]$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83264773ba5e96101d0e6da600da3ec2_l3.png)
- Los vectores de pesos iniciales,
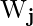 , están dados por
, están dados por - Encontramos la neurona ganadora (mejor coincidencia)
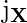 que satisface el criterio euclidiano de distancia mínima:
que satisface el criterio euclidiano de distancia mínima: - La neurona 3 es la ganadora y su vector de pesos
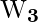 se actualiza siguiendo la regla de aprendizaje competitivo.
se actualiza siguiendo la regla de aprendizaje competitivo. - El vector de peso actualizado
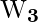 en la iteración
en la iteración 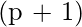 se calcula como:
se calcula como: - El vector de peso
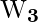 de la neurona ganadora 3 se vuelve más cercano al vector de entrada
de la neurona ganadora 3 se vuelve más cercano al vector de entrada  en cada iteración.
en cada iteración.
![Rendered by QuickLaTeX.com \[$\mathbf{W}_{1}=\left[\begin{array}{l}0.27 \\ 0.81\end{array}\right] \quad \mathbf{W}_{2}=\left[\begin{array}{l}0.42 \\ 0.70\end{array}\right] \quad \mathbf{W}_{3}=\left[\begin{array}{l}0.43 \\ 0.21\end{array}\right]$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-df7740484bc5e6abcc34d5d07cb7f5b1_l3.png)
![Rendered by QuickLaTeX.com \[$d_{1}=\sqrt{\left(x_{1}-w_{11}\right)^{2}+\left(x_{2}-w_{21}\right)^{2}}=\sqrt{(0.52-0.27)^{2}+(0.12-0.81)^{2}}=0.73$\\ $d_{2}=\sqrt{\left(x_{1}-w_{12}\right)^{2}+\left(x_{2}-w_{22}\right)^{2}}=\sqrt{(0.52-0.42)^{2}+(0.12-0.70)^{2}}=0.59$\\ $d_{3}=\sqrt{\left(x_{1}-w_{13}\right)^{2}+\left(x_{2}-w_{23}\right)^{2}}=\sqrt{(0.52-0.43)^{2}+(0.12-0.21)^{2}}=0.13$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4cf9252846f5f2bfa605ee3ae528a989_l3.png)
![Rendered by QuickLaTeX.com \[$\Delta w_{13}=\alpha\left(x_{1}-w_{13}\right)=0.1(0.52-0.43)=0.01$\\ $\Delta w_{23}=\alpha\left(x_{2}-w_{23}\right)=0.1(0.12-0.21)=-0.01$\]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a2fa9951bb31a163be4c815f36091e6_l3.png)
![Rendered by QuickLaTeX.com \[$\mathbf{W}_{3}(p+1)=\mathbf{W}_{3}(p)+\Delta \mathbf{W}_{3}(p)=\left[\begin{array}{l}0.43 \\ 0.21\end{array}\right]+\left[\begin{array}{r}0.01 \\ -0.01\end{array}\right]=\left[\begin{array}{l}0.44 \\ 0.20\end{array}\right]\]$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2b990505ad27e7b0e40e3b736367859d_l3.png)
Publicación traducida automáticamente
Artículo escrito por goodday451999 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA