Requisitos previos: Q-Learning .
En las siguientes derivaciones, se utilizarán los símbolos definidos en el artículo de requisitos previos.
La técnica Q-learning se basa en la Ecuación de Bellman .
![]()
where,
E : Expectation
t+1 : next state![]() : discount factor
: discount factor
Reformulando la ecuación anterior en forma de Q-Value:-
![]()
![]()
El valor Q óptimo viene dado por
![]()
Iteración de políticas: es el proceso de determinar la política óptima para el modelo y consta de los siguientes dos pasos:-
- Evaluación de políticas: este proceso estima el valor de la función de recompensa a largo plazo con la política codiciosa obtenida del último paso de mejora de políticas.
- Mejora de la política: este proceso actualiza la política con la acción que maximiza V para cada estado. Este proceso se repite hasta que se logra la convergencia.
Pasos involucrados: –
- Inicialización:
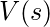 = cualquier número aleatorio real
= cualquier número aleatorio real  = cualquier A(s) elegido arbitrariamente
= cualquier A(s) elegido arbitrariamente - Evaluación de políticas:
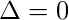 while(
while(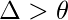 )
{
for each s in S
{
)
{
for each s in S
{
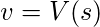

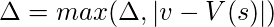 }
}
}
}
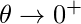
- Mejora de la política:
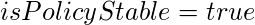 while(true)
for each s in S
{
while(true)
for each s in S
{
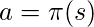
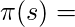 if(
if(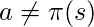 )
)
 if(
if(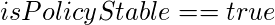 )
break from both loops
}
return V,
)
break from both loops
}
return V,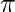
- Iteración de valor: este proceso actualiza la función V de acuerdo con la ecuación óptima de Bellman .
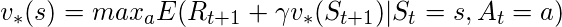
Pasos de trabajo:
- Inicialización: Inicialice la array V por cualquier número real aleatorio.
- Cálculo del valor óptimo:
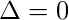 while(
while(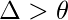 )
{
for each s in S
{
)
{
for each s in S
{

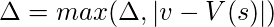 }
}
}
}
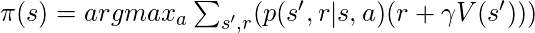 return
return 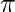
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA