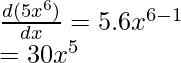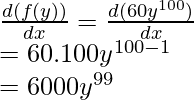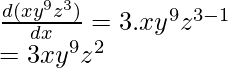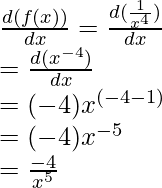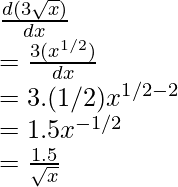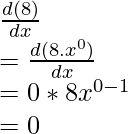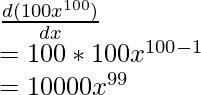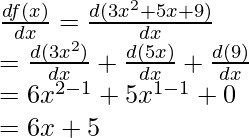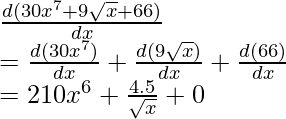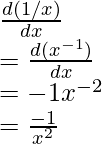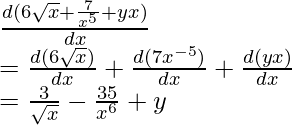La diferenciación de una función consiste en dividir la función en una versión más pequeña y mucho más simple de sí misma. Derivada de cualquier función es diferenciarla con respecto a la variable presente en ella, en palabras más sencillas, las derivadas son la tasa de cambio de cualquier función con respecto a la variable presente en ella. Por ejemplo, cuando se conduce un automóvil demasiado rápido, la policía toma medidas, pero ¿cómo saben que se ha sobrepasado el límite de velocidad? ¿Qué es la velocidad? La velocidad no es más que la derivada de la distancia con respecto al tiempo, si un automóvil es demasiado rápido, está recorriendo más distancia por unidad de tiempo y, por lo tanto, tiene más velocidad.
Este es el ejemplo más básico de cómo funcionan los derivados. Una función puede ser realmente compleja y por lo tanto, se definen algunas reglas para ella, una de esas reglas es la regla de la potencia, veámosla con más detalle.
Regla de poder
La regla de la potencia, como sugiere el nombre, se define para funciones con exponentes presentes, como el cuadrado de la variable o el cubo de la función, etc. funciones complejas también.
Para usar la regla de la potencia, toma el exponente y multiplícalo por el coeficiente de la variable y disminuye el exponente en 1.
La función dada es, ax n
La derivada de esta función usando la regla de la potencia será,
Veamos diferentes tipos de funciones y veamos cómo funciona la regla de la potencia en cada una de ellas, tenga en cuenta que la regla sigue siendo la misma en todas ellas,
Diferenciar polinomios
La fórmula general anterior se define para un polinomio y cualquier polinomio (monomio, binomio, etc.) se puede diferenciar con una regla de potencia.
Ejemplo: Encuentra la derivada de las funciones dadas a continuación,
- f(x) = 5x 6
- f(y) = 60y 100
- f(z) = xy 9 z 3
Solución:
(yo) f(x)= 5x 6
Diferenciando f(x) con x,
(ii) f(y)= 60y 100
Diferenciando f(y) con y,
(iii) f(z)= xy 9 z 3
Diferenciando f(z) con z, aquí una cosa importante a tener en cuenta es que la función tiene z como variable, por lo tanto, xey se tratan como una constante.
Nota: la regla de la potencia se puede aplicar para cualquier función con alguna potencia, por lo general se ve como x n donde n es la potencia o el exponente. Una función en forma de ax n se conoce como funciones de potencia.
¿Se puede aplicar la regla de Poder a las funciones donde el poder no es visible?
SÍ. Cada variable tiene alguna potencia, incluso en ausencia de variables, se puede agregar una variable con una potencia 0 y luego se aplica la regla de la potencia.
Comprendamos el concepto de aplicar la regla de potencia a tales funciones con más detalle,
Diferenciar números negativos
Supongamos que una función tiene potencia negativa o la función se da en forma de fracción (básicamente, la potencia negativa está presente en la función, en tal caso,
- Convierta la fracción en la forma de potencia respectiva.
- Deriva la función usando la regla de la potencia.
- Conviértelo de nuevo a la forma de fracción.
Ejemplo: Encuentra la derivada de la función, f(x) = 1/x 4 .
Solución:
f(x) = 1/x 4
Diferenciando radicales y potencias fraccionarias
Para diferenciar Radicales o potencias fraccionarias, sigue los pasos,
- Convierte radicales en forma de potencia.
- Aplicar la derivada.
- Convertir de nuevo en forma radical.
Ejemplo: Encuentra la derivada de la función, f(x) = 3√x
Solución:
f(x) = 3√x
Diferenciando f(x) con x,
Diferenciar una constante
La derivada de una constante es 0. Incluso una constante se puede diferenciar con la ayuda de la regla de la potencia, ya que agregar una variable con una potencia de 0 no afectará la función/constante. Luego, con la ayuda de la misma variable, usa la regla de la potencia para diferenciar la función.
Ejemplo: Encuentra la derivada de la función, f(x) = 8.
Solución:
f(x) = 8
Problemas de muestra
Pregunta 1: Encuentra la derivada de la función con respecto a x, f(x) = 100x 100
Solución:
f(x) = 100×100
Diferenciando wrt x,
Pregunta 2: Encuentra la derivada de la función dada a continuación,
f(x)= 3x 2 + 5x+ 9
Solución:
f(x)= 3x 2 + 5x+ 9
Diferenciando wrt x,
Pregunta 3: Encuentra la derivada de la función,
f(x)= 30x 7 + 9√x+ 66
Solución:
f(x)= 30x 7 +9√x+66
Diferenciando wrt x,
Pregunta 4: Encuentra la derivada de las funciones dadas,
- f(x)=9
- f(x)=x
- f(x)=z
- f(x)=1/x
- f(x)=√x
Solución:
- f(x)=9
- f(x)=x
- f(x)=z
- f(x)=1/x
Pregunta 5: Encuentra la derivada de la función dada a continuación,
f(x)= 6√x+ 7/x 5 + yx
Solución:
f(x)= 6√x+ 7/x 5 + yx
Diferenciando wrt x,
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA