Apotema de un polígono regular de n lados

Dada aquí la longitud del lado a de un polígono regular de n lados, la tarea es encontrar la longitud de su apotema. 
Apotema es la línea trazada desde el centro del polígono que es perpendicular a uno de sus lados. 
Ejemplos: 
 

Input a = 9, n = 6
Output: 7.79424

Input: a = 8, n = 7
Output: 8.30609

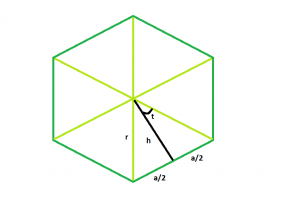
Enfoque : 
 

En la figura vemos que el polígono se puede dividir en n triángulos iguales. 
Mirando uno de los triángulos, vemos que el ángulo completo en el centro se puede dividir en = 360/n 
Entonces, el ángulo t = 180/n 
ahora, tan t = a/2h 
Entonces, h = a/(2*tan t ) 
aquí, h es la apotema, 
entonces, apotema = a/(2*tan(180/n))

A continuación se muestra la implementación del enfoque anterior.
 

// C++ Program to find the apothem
// of a regular polygon with given side length
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the apothem
// of a regular polygon
float polyapothem(float n, float a)
{
 
    // Side and side length cannot be negative
    if (a < 0 && n < 0)
        return -1;
 
    // Degree converted to radians
    return a / (2 * tan((180 / n) * 3.14159 / 180));
}
 
// Driver code
int main()
{
    float a = 9, n = 6;
    cout << polyapothem(n, a) << endl;
 
    return 0;
}

// Java Program to find the apothem of a
// regular polygon with given side length
import java.util.*;
 
class GFG
{
 
    // Function to find the apothem
    // of a regular polygon
    double polyapothem(double n, double a)
    {
 
        // Side and side length cannot be negative
        if (a < 0 && n < 0)
            return -1;
 
        // Degree converted to radians
        return (a / (2 * java.lang.Math.tan((180 / n)
                * 3.14159 / 180)));
    }
 
// Driver code
public static void main(String args[])
{
    double a = 9, n = 6;
    GFG g=new GFG();
    System.out.println(g.polyapothem(n, a));
}
 
}
//This code is contributed by Shivi_Aggarwal

# Python 3 Program to find the apothem
# of a regular polygon with given side
# length
from math import tan
 
# Function to find the apothem
# of a regular polygon
def polyapothem(n, a):
     
    # Side and side length cannot be negative
    if (a < 0 and n < 0):
        return -1
 
    # Degree converted to radians
    return a / (2 * tan((180 / n) *
                   3.14159 / 180))
 
# Driver code
if __name__ == '__main__':
    a = 9
    n = 6
    print('{0:.6}'.format(polyapothem(n, a)))
     
# This code is contributed by
# Sahil_Shelangia

// C# Program to find the apothem of a
// regular polygon with given side length
using System;
 
class GFG
{
 
// Function to find the apothem
// of a regular polygon
static double polyapothem(double n,
                          double a)
{
 
    // Side and side length cannot
    // be negative
    if (a < 0 && n < 0)
        return -1;
 
    // Degree converted to radians
    return (a / (2 * Math.Tan((180 / n) *
                       3.14159 / 180)));
}
 
// Driver code
public static void Main()
{
    double a = 9, n = 6;
    Console.WriteLine(Math.Round(polyapothem(n, a), 4));
}
}
 
// This code is contributed by Ryuga

<?php
// PHP Program to find the apothem of a
// regular polygon with given side length
 
// Function to find the apothem
// of a regular polygon
function polyapothem($n, $a)
{
 
    // Side and side length cannot
    // be negative
    if ($a < 0 && $n < 0)
        return -1;
 
    // Degree converted to radians
    return $a / (2 * tan((180 / $n) *
                    3.14159 / 180));
}
 
// Driver code
$a = 9; $n = 6;
echo polyapothem($n, $a) . "\n";
 
// This code is contributed
// by Akanksha Rai
?>

<script>
// javascript Program to find the apothem of a
// regular polygon with given side length
 
// Function to find the apothem
// of a regular polygon
function polyapothem(n , a)
{
 
    // Side and side length cannot be negative
    if (a < 0 && n < 0)
        return -1;
 
    // Degree converted to radians
    return (a / (2 * Math.tan((180 / n)
            * 3.14159 / 180)));
}
 
// Driver code
 
var a = 9, n = 6;
 
document.write(polyapothem(n, a).toFixed(5));
 
 
// This code contributed by Princi Singh
</script>

7.79424

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)