Cuantificación de vectores de aprendizaje

Learning Vector Quantization (o LVQ) es un tipo de red neuronal artificial que también se inspira en modelos biológicos de sistemas neuronales. Se basa en un prototipo de algoritmo de clasificación de aprendizaje supervisado y entrenó su red a través de un algoritmo de aprendizaje competitivo similar a Self Organizing Map. También puede tratar el problema de clasificación multiclase. LVQ tiene dos capas, una es la capa de Entrada y la otra es la capa de Salida. La arquitectura de la cuantificación del vector de aprendizaje con el número de clases en los datos de entrada y el número n de características de entrada para cualquier muestra se muestra a continuación: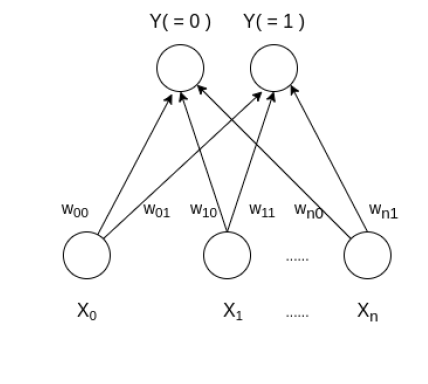

¿Cómo funciona la cuantificación del vector de aprendizaje?

Digamos que una entrada de datos de tamaño ( m, n ) donde m es el número de ejemplos de entrenamiento y n es el número de funciones en cada ejemplo y un vector de etiqueta de tamaño ( m, 1 ). Primero, inicializa los pesos de tamaño ( n, c ) del primer número c de muestras de entrenamiento con diferentes etiquetas y debe descartarse de todas las muestras de entrenamiento. Aquí, c es el número de clases. Luego itere sobre los datos de entrada restantes, para cada ejemplo de entrenamiento, actualiza el vector ganador (vector de peso con la distancia más corta (por ejemplo, distancia euclidiana) del ejemplo de entrenamiento). 

La regla de actualización del peso viene dada por:

if correctly_classified:
wij(new) = wij(old) + alpha(t) * (xik - wij(old))
else:
wij(new) = wij(old) - alpha(t) * (xik - wij(old))

donde alfa es una tasa de aprendizaje en el tiempo t, j denota el vector ganador, i denota la i ^-ésima característica del ejemplo de entrenamiento yk denota el k ^-ésimo ejemplo de entrenamiento de los datos de entrada. Después de entrenar la red LVQ, los pesos entrenados se utilizan para clasificar nuevos ejemplos. Un nuevo ejemplo está etiquetado con la clase del vector ganador.

Algoritmo

Los pasos involucrados son:

• Inicialización de peso
• Para 1 a N número de épocas
• Seleccione un ejemplo de entrenamiento
• Calcule el vector ganador
• Actualizar el vector ganador
• Repita los pasos 3, 4, 5 para todos los ejemplos de entrenamiento.
• Clasificar muestra de prueba

A continuación se muestra la implementación. 

import math
 
 
class LVQ :
     
    # Function here computes the winning vector
    # by Euclidean distance
    def winner( self, weights, sample ) :
         
        D0 = 0
        D1 = 0
         
        for i  in range( len( sample ) ) :
            D0 = D0 + math.pow( ( sample[i] - weights[0][i] ), 2 )
            D1 = D1 + math.pow( ( sample[i] - weights[1][i] ), 2 )
             
        if D0 > D1 :
            return 0
        else :
            return 1
 
    # Function here updates the winning vector    
    def update( self, weights, sample, J, alpha, actual ) :
          if actual -- j:
            for i in range(len(weights)) :
                weights[J][i] = weights[J][i] + alpha * ( sample[i] - weights[J][i] )
        else:
            for i in range(len(weights)) :
                weights[J][i] = weights[J][i] - alpha * ( sample[i] - weights[J][i] )
 
# Driver code
def main() :
 
    # Training Samples ( m, n ) with their class vector
    X =  [[ 0, 0, 1, 1 ],  [ 1, 0, 0, 0 ],
          [ 0, 0, 0, 1 ], [ 0, 1, 1, 0 ],
          [ 1, 1, 0, 0 ], [ 1, 1, 1, 0 ],]
 
    Y = [ 0, 1, 0, 1, 1, 1 ]
    m, n = len( X ), len( X[0] )
     
    # weight initialization ( n, c )
    weights = []
    weights.append( X.pop( 0 ) )
    weights.append( X.pop( 0 ) )
 
    # Samples used in weight initialization will
    # not use in training
    m = m - 2
    Y.pop(0)
    Y.pop(0)
     
    # training
    ob = LVQ()
    epochs = 3
    alpha = 0.1
     
    for i in range( epochs ) :
        for j in range( m ) :
             
            # Sample selection
            T = X[j]
             
            # Compute winner
            J = ob.winner( weights, T )
         
            # Update weights
            ob.update( weights, T, J, alpha , Y[j])
             
    # classify new input sample
    T = [ 0, 0, 1, 0 ]
    J = ob.winner( weights, T )
    print( "Sample T belongs to class : ", J )
    print( "Trained weights : ", weights )
     
if __name__ == "__main__":
    main()