Área de un pentagrama regular

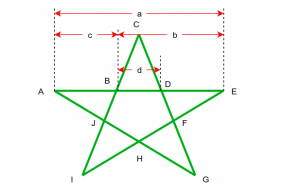
Dado un pentagrama y la longitud de su lado interno (d). La tarea es averiguar el área de Pentagram. El Pentagrama es una estrella de cinco puntas que se forma dibujando una línea continua en cinco segmentos rectos.

Ejemplos: 

Entrada: d = 5 
Salida: Área = 139,187 
Área del pentagrama regular = 139,187 

Entrada: d = 7 
Salida: Área = 272.807 
 

La idea es utilizar la proporción áurea entre a/b, b/c y c/d, que equivale aproximadamente a 1,618. 
La longitud del lado interior d se da, por lo que 
c = 1,618 * d 
b = 1,618 * c 
a = 1,618 * b
AB, BC y CD son iguales (ambos lados del pentagrama regular) 
Entonces AB = BC = CD = c y BD está dada por d.

Área del pentagrama = Área del Pentágono BDFHJ + 5 * (Área del triángulo BCD) 
Área del Pentágono BDFHJ = (d^2 * 5)/ (4* tan 36) 
Área del triángulo BCD = [s(sd)(sc)( sc)]^(1/2) {Fórmula de Heron} 
donde 
s = (d + c + c)/2 
 

A continuación se muestra la implementación del enfoque anterior: 

// C++ implementation of the approach
#include <bits/stdc++.h>
#define PI 3.14159
using namespace std;
 
// Function to return the area of triangle BCD
double areaOfTriangle(float d)
{
    // Using Golden ratio
    float c = 1.618 * d;
    float s = (d + c + c) / 2;
 
    // Calculate area of triangle BCD
    double area = sqrt(s * (s - c) *
                          (s - c) * (s - d));
 
    // Return area of all 5 triangle are same
    return 5 * area;
}
 
// Function to return the area of regular pentagon
double areaOfRegPentagon(float d)
{
    // Calculate the area of regular
    // pentagon using above formula
    double cal = 4 * tan(PI / 5);
    double area = (5 * d * d) / cal;
 
    // Return area of regular pentagon
    return area;
}
 
// Function to return the area of pentagram
double areaOfPentagram(float d)
{
    // Area of a pentagram is equal to the
    // area of regular  pentagon and five times
    // the area of Triangle
    return areaOfRegPentagon(d) +
                             areaOfTriangle(d);
}
 
// Driver code
int main()
{
    float d = 5;
    cout << areaOfPentagram(d) << endl;
 
    return 0;
}

// Java implementation of above approach
public class GFG
{
 
    static double PI = 3.14159;
 
    // Function to return the area of triangle BCD
    static double areaOfTriangle(float d)
    {
        // Using Golden ratio
        float c = (float) (1.618 * d);
        float s = (d + c + c) / 2;
 
        // Calculate area of triangle BCD
        double area = Math.sqrt(s * (s - c)
                * (s - c) * (s - d));
 
        // Return area of all 5 triangle are same
        return 5 * area;
    }
 
    // Function to return the area of regular pentagon
    static double areaOfRegPentagon(float d)
    {
        // Calculate the area of regular
        // pentagon using above formula
        double cal = 4 * Math.tan(PI / 5);
        double area = (5 * d * d) / cal;
 
        // Return area of regular pentagon
        return area;
    }
 
    // Function to return the area of pentagram
    static double areaOfPentagram(float d)
    {
        // Area of a pentagram is equal to the
        // area of regular pentagon and five times
        // the area of Triangle
        return areaOfRegPentagon(d)
                + areaOfTriangle(d);
    }
 
    // Driver code
    public static void main(String[] args)
    {
        float d = 5;
        System.out.println(areaOfPentagram(d));
    }
}
 
// This code has been contributed by 29AjayKumar

# Python3 implementation of the approach
 
import math
 
PI = 3.14159
 
# Function to return the area of triangle BCD
def areaOfTriangle(d) :
 
    # Using Golden ratio
    c = 1.618 * d
    s = (d + c + c) / 2
 
    # Calculate area of triangle BCD
    area = math.sqrt(s * (s - c) *
                        (s - c) * (s - d))
 
    # Return area of all 5 triangles are the same
    return 5 * area
 
 
# Function to return the area of regular pentagon
def areaOfRegPentagon(d) :
     
    global PI
    # Calculate the area of regular
    # pentagon using above formula
    cal = 4 * math.tan(PI / 5)
    area = (5 * d * d) / cal
     
    # Return area of regular pentagon
    return area
 
 
# Function to return the area of pentagram
def areaOfPentagram(d) :
 
    # Area of a pentagram is equal to the
    # area of regular pentagon and five times
    # the area of Triangle
    return areaOfRegPentagon(d) + areaOfTriangle(d)
 
 
# Driver code
 
d = 5
print(areaOfPentagram(d))
 
     
# This code is contributed by ihritik

// C# implementation of the above approach
using System;
 
class GFG
{
 
    static double PI = 3.14159;
 
    // Function to return the area of triangle BCD
    static double areaOfTriangle(float d)
    {
        // Using Golden ratio
        float c = (float) (1.618 * d);
        float s = (d + c + c) / 2;
 
        // Calculate area of triangle BCD
        double area = Math.Sqrt(s * (s - c)
                * (s - c) * (s - d));
 
        // Return area of all 5 triangle are same
        return 5 * area;
    }
 
    // Function to return the area of regular pentagon
    static double areaOfRegPentagon(float d)
    {
        // Calculate the area of regular
        // pentagon using above formula
        double cal = 4 * Math.Tan(PI / 5);
        double area = (5 * d * d) / cal;
 
        // Return area of regular pentagon
        return area;
    }
 
    // Function to return the area of pentagram
    static double areaOfPentagram(float d)
    {
        // Area of a pentagram is equal to the
        // area of regular pentagon and five times
        // the area of Triangle
        return areaOfRegPentagon(d)
                + areaOfTriangle(d);
    }
 
    // Driver code
    public static void Main()
    {
        float d = 5;
        Console.WriteLine(areaOfPentagram(d));
    }
}
 
// This code has been contributed by ihritik

<script>
// Javascript implementation of the approach
var PI = 3.14159
 
// Function to return the area of triangle BCD
function areaOfTriangle(d)
{
    // Using Golden ratio
    var c = 1.618 * d;
    var s = (d + c + c) / 2;
 
    // Calculate area of triangle BCD
    var area = Math.sqrt(s * (s - c) *
                          (s - c) * (s - d));
 
    // Return area of all 5 triangle are same
    return 5 * area;
}
 
// Function to return the area of regular pentagon
function areaOfRegPentagon( d)
{
    // Calculate the area of regular
    // pentagon using above formula
    var cal = 4 * Math.tan(PI / 5);
    var area = (5 * d * d) / cal;
 
    // Return area of regular pentagon
    return area;
}
 
// Function to return the area of pentagram
function areaOfPentagram(d)
{
    // Area of a pentagram is equal to the
    // area of regular  pentagon and five times
    // the area of Triangle
    return areaOfRegPentagon(d) +
                             areaOfTriangle(d);
}
 
// Driver code
var d = 5;
document.write(areaOfPentagram(d).toFixed(3));
 
// This code is contributed by ShubhamSingh10
</script>

139.187

Complejidad de tiempo : O(1)

Espacio Auxiliar: O(1)