Área de un polígono con n vértices ordenados dados

Posted on by Rudeus Greyrat

Dadas las coordenadas ordenadas de un polígono de n vértices. Encuentra el área del polígono. Aquí ordenado significa que las coordenadas se dan en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj desde el primer vértice hasta el último.
Ejemplos: 

Input :  X[] = {0, 4, 4, 0}, Y[] = {0, 0, 4, 4};
Output : 16

Input : X[] = {0, 4, 2}, Y[] = {0, 0, 4}
Output : 8

Podemos calcular el área de un polígono usando la fórmula Shoelace .  

Área

=\frac{1}{2}\left | \sum_{i=1}^{n-1}x_iy_(_i+_1_)+x_ny1-\sum_{i=1}^{n-1}x_(_i+_1_)y_i-x_1y_n \right |

= | 1/2 [ (x 1 y 2 + x 2 y 3 + … + x n-1 y n + x n y 1 ) –

(x 2 y 1 + x 3 y 2 + … + x n y n-1 + x 1 y n ) ] |

La fórmula anterior se obtiene siguiendo el producto cruzado de los vértices para obtener el área de los triángulos formados en el polígono. 
A continuación se muestra una implementación de la fórmula anterior. 

CPP

// C++ program to evaluate area of a polygon using
// shoelace formula
#include <bits/stdc++.h>
using namespace std;
 
// (X[i], Y[i]) are coordinates of i'th point.
double polygonArea(double X[], double Y[], int n)
{
    // Initialize area
    double area = 0.0;
 
    // Calculate value of shoelace formula
    int j = n - 1;
    for (int i = 0; i < n; i++)
    {
        area += (X[j] + X[i]) * (Y[j] - Y[i]);
        j = i;  // j is previous vertex to i
    }
 
    // Return absolute value
    return abs(area / 2.0);
}
 
// Driver program to test above function
int main()
{
    double X[] = {0, 2, 4};
    double Y[] = {1, 3, 7};
 
    int n = sizeof(X)/sizeof(X[0]);
 
    cout << polygonArea(X, Y, n);
}

Java

// Java program to evaluate area
// of a polygon using shoelace formula
import java.io.*;
 
class GFG
{
    // (X[i], Y[i]) are coordinates of i'th point.
    public static double polygonArea(double X[], double Y[],
                                                       int n)
    {
        // Initialize area
        double area = 0.0;
     
        // Calculate value of shoelace formula
        int j = n - 1;
        for (int i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);
             
            // j is previous vertex to i
            j = i;
        }
     
        // Return absolute value
        return Math.abs(area / 2.0);
    }
 
    // Driver program
    public static void main (String[] args)
    {
        double X[] = {0, 2, 4};
        double Y[] = {1, 3, 7};
     
        int n = 3;
        System.out.println(polygonArea(X, Y, n));
    }
 
}
// This code is contributed by Sunnnysingh

Python3

# python3 program to evaluate
# area of a polygon using
# shoelace formula
 
# (X[i], Y[i]) are coordinates of i'th point.
def polygonArea(X, Y, n):
 
    # Initialize area
    area = 0.0
 
    # Calculate value of shoelace formula
    j = n - 1
    for i in range(0,n):
        area += (X[j] + X[i]) * (Y[j] - Y[i])
        j = i   # j is previous vertex to i
     
 
    # Return absolute value
    return int(abs(area / 2.0))
 
# Driver program to test above function
X = [0, 2, 4]
Y = [1, 3, 7]
n = len(X)
print(polygonArea(X, Y, n))
 
# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# program to evaluate area
// of a polygon using shoelace formula
using System;
 
class GFG {
     
    // (X[i], Y[i]) are coordinates of i'th point.
    public static double polygonArea(double[] X,
                               double[] Y, int n)
    {
         
        // Initialize area
        double area = 0.0;
 
        // Calculate value of shoelace formula
        int j = n - 1;
         
        for (int i = 0; i < n; i++) {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);
 
            // j is previous vertex to i
            j = i;
        }
 
        // Return absolute value
        return Math.Abs(area / 2.0);
    }
 
    // Driver program
    public static void Main()
    {
        double[] X = { 0, 2, 4 };
        double[] Y = { 1, 3, 7 };
 
        int n = 3;
        Console.WriteLine(polygonArea(X, Y, n));
    }
}
 
// This code is contributed by vt_m.

PHP

<?php
// PHP program to evaluate area of
// a polygon using shoelace formula
 
// (X[i], Y[i]) are
// coordinates of i'th point.
function polygonArea($X, $Y, $n)
{
    // Initialize area
    $area = 0.0;
 
    // Calculate value of
    // shoelace formula
    $j = $n - 1;
    for ($i = 0; $i < $n; $i++)
    {
        $area += ($X[$j] + $X[$i]) *
                 ($Y[$j] - $Y[$i]);
                  
        // j is previous vertex to i        
        $j = $i;
    }
 
    // Return absolute value
    return abs($area / 2.0);
}
 
// Driver Code
$X = array(0, 2, 4);
$Y = array(1, 3, 7);
 
$n = sizeof($X);
 
echo polygonArea($X, $Y, $n);
 
// This code is contributed by ajit
?>

Javascript

<script>
 
// JavaScript program to evaluate area
// of a polygon using shoelace formula
  
    // (X[i], Y[i]) are coordinates of i'th point.
    function polygonArea(X, Y, n)
    {
        // Initialize area
        let area = 0.0;
      
        // Calculate value of shoelace formula
        let j = n - 1;
        for (let i = 0; i < n; i++)
        {
            area += (X[j] + X[i]) * (Y[j] - Y[i]);
              
            // j is previous vertex to i
            j = i;
        }
      
        // Return absolute value
        return Math.abs(area / 2.0);
    }
 
// Driver Code
 
        let X = [0, 2, 4];
        let Y = [1, 3, 7];
      
        let n = 3;
        document.write(polygonArea(X, Y, n));
     
// This code is contributed by target_2.   
</script>

Producción : 

2

Complejidad Temporal: O(n) 
Espacio Auxiliar: O(1), ya que no se ha tomado ningún espacio extra.

¿Por qué se llama Shoelace Formula?  
La fórmula se llama así por la forma en que la evaluamos. 
Ejemplo : 

Let the input vertices be
 (0, 1), (2, 3), and (4, 7). 

Evaluation procedure matches with process of tying
shoelaces.

We write vertices as below
  0    1
  2    3
  4    7
  0    1  [written twice]

we evaluate positive terms as below
  0  \  1
  2  \  3
  4  \  7
  0     1  
i.e., 0*3 + 2*7 + 4*1 = 18 

we evaluate negative terms as below
  0     1
  2  /  3
  4  /  7
  0  /  1  
i.e., 0*7 + 4*3 + 2*1 = 14

Area = 1/2 (18 - 14) = 2 

See this for a clearer image.

¿Como funciona esto?  
Siempre podemos dividir un polígono en triángulos. La fórmula del área se obtiene tomando cada arista AB y calculando el área (con signo) del triángulo ABO con un vértice en el origen O, tomando el producto vectorial (que da el área de un paralelogramo) y dividiendo por 2. Como uno envuelve el polígono, estos triángulos con áreas positivas y negativas se superpondrán, y las áreas entre el origen y el polígono se cancelarán y sumarán 0, mientras que solo permanecerá el área dentro del triángulo de referencia. [Fuente: wiki ] 

Para una mejor comprensión, observe los siguientes diagramas:

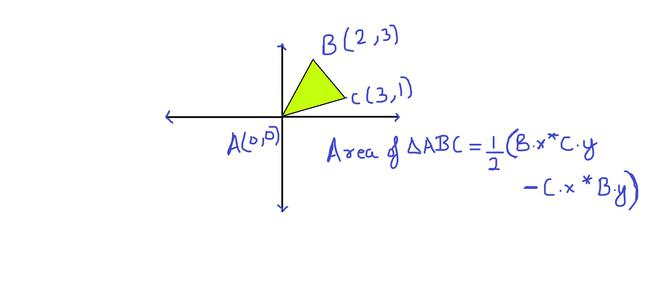
Area Of Triangle Using Cross Product

área de triángulo usando producto cruzado

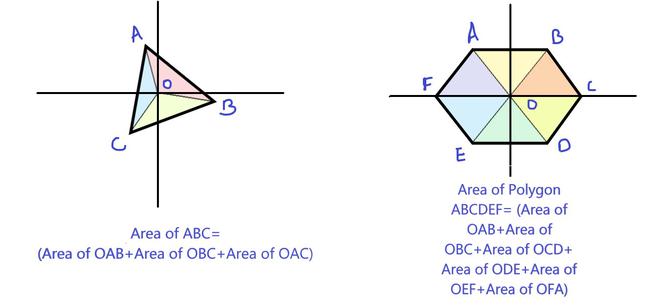
Dividing Polygons into Smaller Triangles to compute Area

Dividir polígonos en triángulos más pequeños para calcular el área

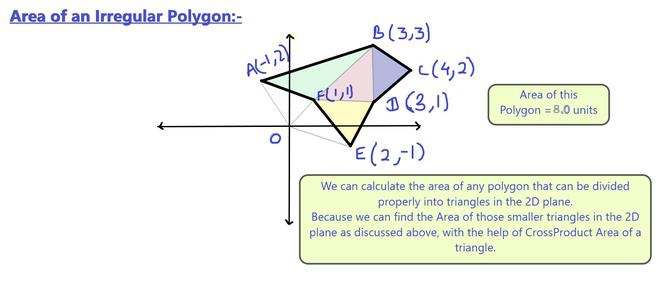
for Irregular Polygons, we can form triangles to compute the Area

De manera similar, para polígonos irregulares, podemos formar triángulos para calcular el área

Artículos relacionados: 
Triangulación de polígonos de costo mínimo  
Encuentra una ruta cerrada simple para un conjunto dado de puntos
Este artículo es una contribución de Aarti_Rathi y Utkarsh Trivedi. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *