Área entre dos curvas – Barcelona Geeks

La integración es un proceso de calcular el área de una región particular en muchas tiras pequeñas y luego calcular su área y sumarlas. Conocemos las fórmulas para calcular las áreas de algunas formas estándar, la integración nos permite calcular el área de cualquier región arbitraria dada la ecuación de sus límites. A veces, en escenarios más complejos, necesitamos encontrar las áreas entre las intersecciones de algunas curvas. Así que tenemos que aprender a calcular el área entre dos curvas. Veamos cómo resolver tales problemas,

Fórmula para el área entre curvas

Digamos que tenemos dos curvas dadas en la siguiente figura por f(x) y g(x) . Sabemos que f(x) ≥ g(x) en el intervalo [a, b]. Nuestro objetivo es encontrar el área delimitada entre dos curvas en el intervalo dado. Primero, encontramos los puntos de intersección entre dos curvas. Los puntos de intersección son x = a y x = b. En la siguiente figura, la región sombreada representa el área delimitada entre dos curvas. Suponemos una franja elemental entre las curvas, la longitud de esta franja es f(x) – g(x), y el ancho es dx. Entonces, el área acotada entre dos curvas será,

$A = \int^{b}_a[f(x) - g(x)]dx$

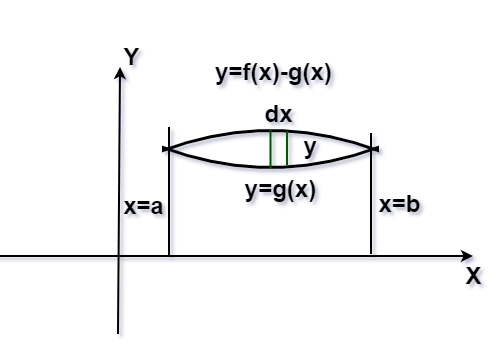
En la formulación anterior asumimos que f(x) ≥ g(x) en el intervalo [a, b]. Pero no siempre es así, consideremos otro caso, f(x) ≥ g(x) en [a, c] y f(x) ≤ g(x) en [c, b], aquí a < c < b . Entonces, el área delimitada en esta región se da en la siguiente figura,

Área Total = Área de PRQS + Área de QACB

= $\int^{c}_{a}[f(x) - g(x)]dx + \int^{b}_{c}[g(x) - f(x)]dx$

Problemas de muestra

Pregunta 1: Encuentra el área delimitada entre dos rectas f(x) = 5x y g(x) = 3x de x =0 a x = 3.

Solución:

La siguiente figura muestra ambas líneas,

Figura

Área = $\int^{b}_a[f(x) - g(x)]dx$

= $\int^{3}_0[f(x) - g(x)]dx$

= $\int^{3}_0[5x - 3x]dx$

= $\int^{3}_0[2x]dx$

= $[x^2]^3_0$

= 9

Pregunta 2: Encuentra el área acotada entre dos curvas f(x) = x ³ y g(x) = x ² entre 0 y 1.

Solución:

La siguiente figura muestra ambas curvas, para encontrar la región acotada, primero necesitamos encontrar las intersecciones.

f(x) = g(x)

⇒ x ³ = x ²

⇒x ² (x-1) = 0

⇒ x = 0 y 1

Figura

Área = $\int^{b}_a[f(x) - g(x)]dx$

= $\int^{1}_0[f(x) - g(x)]dx$

= $\int^{3}_0[x^2 - x^3]dx$

= $\int^{1}_{0}x^2dx - \int^1_0x^3dx$

= $[\frac{x^3}{3}]^1_0 - [\frac{x^4}{4}]^1_0$

= $\frac{1}{3} - \frac{1}{4}$

= $\frac{1}{12}$

Pregunta 3: Encuentra el área delimitada entre la parábola y ² = 4x y x ² + y ² = 9.

Solución:

La siguiente figura muestra ambas curvas, para encontrar la región acotada, primero necesitamos encontrar las intersecciones.

x2 + ^y2⁼ 12

Figura

Área = $\int^{b}_a[f(x) - g(x)]dx$

= $\int^{1}_0[f(x) - g(x)]dx$

= $\int^{1}_0[x - x^2]dx$

= $\int^{1}_{0}xdx - \int^1_0x^2dx$

= $[\frac{x^2}{2}]^1_0 - [\frac{x^3}{3}]^1_0$

= $\frac{1}{2} - \frac{1}{3}$

= $\frac{1}{6}$

Pregunta 4: Encuentra el área delimitada entre la parábola y ² = 4x, y su lado recto.

Solución:

La siguiente figura muestra la parábola y su lado recto. Latus rectum es la línea x = 1. Necesitamos encontrar las intersecciones,

y ² = 4

y = 2 y -2

Area = 2(Área de la región delimitada por la parábola y x = 1 y eje x en el primer cuadrante)

= 2( $\int^1_0ydx$

= 2 $\int^1_0\sqrt{4x}dx$

= 4 $\int^1_0\sqrt{x}dx$

= 4 $\int^1_0[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}]dx$

= $\frac{8}{3}[x^{\frac{3}{2}}]^1_0$

= $\frac{8}{3}$

Pregunta 5: La siguiente figura muestra una elipse 9x ² + y ² = 36 y una cuerda PQ. Encuentra el área encerrada entre la cuerda y la elipse en el primer cuadrante.

Solución:

La ecuación de la elipse es,

$\frac{x^2}{4} + \frac{y^2}{36} = 1$

= $\frac{x^2}{2^2} + \frac{y^2}{6^2} = 1$

Entonces, ahora la ecuación de la cuerda se convierte en,

$\frac{x}{2} + \frac{y}{6} = 1$

⇒ 3x + y = 6

⇒ y = 6 – 3x

Entonces, ahora será el área requerida.

un = $3\int^{2}_0 \sqrt{4 - x^2}dx - \int^{2}_{0}(6 - 3x)dx$

= $3[\frac{x}{2}\sqrt{4 - x^2} + 2sin^{-1}\frac{x}{2}]^2_0 - [6x - \frac{3x^2}{2}]^2_0$

= $6sin^{-1}(1) - 6$

= $3\pi - 6$