Dados dos enteros positivos h y w que representan la altura h y el ancho w que forma un rectángulo. Además, hay dos arrays de enteros horizontalCuts y verticalCuts donde horizontalCuts[i] es la distancia desde la parte superior del rectángulo hasta el i-ésimo corte horizontal y, de manera similar, verticalCuts[j] es la distancia desde la izquierda del rectángulo hasta la j-ésima vertical Corte. La tarea es encontrar el área máxima del rectángulo después de cortar en cada posición horizontal y vertical provista en las arrays cortes horizontales y cortes verticales . Dado que la respuesta puede ser un número enorme, devuelve este módulo 10^9 + 7.
Ejemplos:
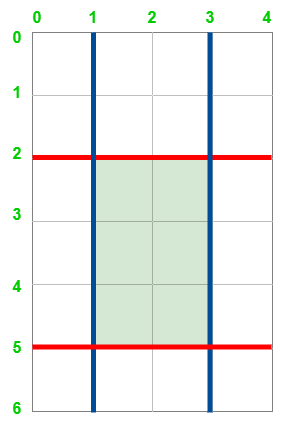
área máxima = 6
Entrada: h = 6, w = 4, cortes horizontales = [2, 5], cortes verticales = [1, 3]
Salida: 6
Explicación: La figura de arriba representa el rectángulo dado. Las líneas rojas son los cortes horizontales y las líneas azules son los cortes verticales. Después de cortar el rectángulo, la parte verde del rectángulo tiene el área máxima.Entrada: h = 5, w = 4, cortes horizontales = [3, 1], cortes verticales = [1]
Salida: 9
Enfoque: El problema se puede resolver observando que-
- Los cortes horizontales son perpendiculares a cualquier corte vertical, entonces todos los cortes verticales cruzan todos los cortes horizontales.
- A continuación, el área máxima del rectángulo debe estar delimitada por al menos un corte vertical y uno horizontal.
De la observación anterior, está claro que necesitamos encontrar la distancia máxima entre dos cortes horizontales y dos cortes verticales respectivamente, y multiplicarlos para encontrar el área del rectángulo. Siga los pasos a continuación para resolver el problema:
- Ordene la array tanto horizontalCuts como verticalCuts .
- Inicialice dos variables, digamos MaxHorizontal y MaxVertical como horizontalCuts[0] y verticalCuts[0] respectivamente, para considerar los rectángulos más cercanos hacia el eje tanto horizontal como verticalmente, lo que almacenará las longitudes máximas horizontal y vertical del rectángulo respectivamente.
- Iterar en el rango [1, horizontalCuts.size()-1] usando la variable i y realizar los siguientes pasos:
- Modifique el valor de MaxHorizontal como max(MaxHorizontal, horizontalCuts[i] – horizontalCuts[i-1]) .
- Modifique el valor de MaxVertical como max(MaxVertical, verticalCuts[i] – verticalCuts[i-1]) .
- Imprima MaxHorizontal*MaxVertical como respuesta.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ Program for the above approach
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
class Solution {
public:
// Returns the maximum area of rectangle
// after Horizontal and Vertical Cuts
int maxArea(int h, int w, vector<int>& horizontalCuts,
vector<int>& verticalCuts)
{
// Sort the two arrays
sort(horizontalCuts.begin(), horizontalCuts.end());
sort(verticalCuts.begin(), verticalCuts.end());
// Insert the right bound h and w
// in their respective vectors
horizontalCuts.push_back(h);
verticalCuts.push_back(w);
//Initialising both by first indexs,
//to consider first rectangle formed by
//respective horizontal and vertical cuts
int maxHorizontal = horizontalCuts[0];
int maxVertical = verticalCuts[0];
// Find the maximum Horizontal Length possible
for (int i = 1; i < horizontalCuts.size(); i++) {
int diff
= horizontalCuts[i] - horizontalCuts[i - 1];
maxHorizontal = max(maxHorizontal, diff);
}
// Find the maximum vertical Length possible
for (int i = 1; i < verticalCuts.size(); i++) {
int diff
= verticalCuts[i] - verticalCuts[i - 1];
maxVertical = max(maxVertical, diff);
}
// Return the maximum area of rectangle
return (int)((long)maxHorizontal * maxVertical
% mod);
}
};
// Driver Code
int main()
{
// Class Call
Solution ob;
// Given Input
vector<int> hc = { 2, 5 }, vc = { 1, 3 };
int h = 6, v = 4;
// Function Call
cout << (ob.maxArea(6, 4, hc, vc));
return 0;
}
Java
// Java program for above approach
import java.awt.*;
import java.util.*;
class GFG{
final int mod = (int) (1e9 + 7);
// Returns the maximum area of rectangle
// after Horizontal and Vertical Cuts
int maxArea(int h, int w, ArrayList<Integer> horizontalCuts,
ArrayList<Integer> verticalCuts)
{
// Sort the two arrays
Collections.sort(horizontalCuts);
Collections.sort(verticalCuts);
// Insert the right bound h and w
// in their respective vectors
horizontalCuts.add(h);
verticalCuts.add(w);
int maxHorizontal = 0;
int maxVertical = 0;
// Find the maximum Horizontal Length possible
for (int i = 1; i < horizontalCuts.size(); i++) {
int diff
= horizontalCuts.get(i) - horizontalCuts.get(i-1);
maxHorizontal = Math.max(maxHorizontal, diff);
}
// Find the maximum vertical Length possible
for (int i = 1; i < verticalCuts.size(); i++) {
int diff
= verticalCuts.get(i) - verticalCuts.get(i - 1);
maxVertical = Math.max(maxVertical, diff);
}
// Return the maximum area of rectangle
return (int)((long)maxHorizontal * maxVertical
% mod);
}
// Driver Code
public static void main(String[] args)
{
// Class Call
GFG ob = new GFG();
// Given Input
ArrayList<Integer> hc = new ArrayList<>();
hc.add(2);
hc.add(5);
ArrayList<Integer> vc = new ArrayList<>();
vc.add(1);
vc.add(3);
int h = 6, v = 4;
// Function Call
System.out.println(ob.maxArea(6, 4, hc, vc));
}
}
//This code is contributed by hritikrommie.
Python3
# python 3 Program for the above approach mod = 1000000007 # Returns the maximum area of rectangle # after Horizontal and Vertical Cuts def maxArea(h, w, horizontalCuts, verticalCuts): # Sort the two arrays horizontalCuts.sort() verticalCuts.sort() # Insert the right bound h and w # in their respective vectors horizontalCuts.append(h) verticalCuts.append(w) maxHorizontal = 0 maxVertical = 0 # Find the maximum Horizontal Length possible for i in range(1, len(horizontalCuts)): diff = horizontalCuts[i] - horizontalCuts[i - 1] maxHorizontal = max(maxHorizontal, diff) # Find the maximum vertical Length possible for i in range(1, len(verticalCuts)): diff = verticalCuts[i] - verticalCuts[i - 1] maxVertical = max(maxVertical, diff) # Return the maximum area of rectangle return (int)(maxHorizontal * maxVertical % mod) # Driver Code if __name__ == "__main__": # Given Input hc = [2, 5] vc = [1, 3] h = 6 v = 4 # Function Call print(maxArea(6, 4, hc, vc)) # This code is contributed by ukasp.
C#
// C# Program for the above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG
{
static int mod = 1000000007;
// Returns the maximum area of rectangle
// after Horizontal and Vertical Cuts
static int maxArea(int h, int w, List<int> horizontalCuts, List<int> verticalCuts)
{
// Sort the two arrays
horizontalCuts.Sort();
verticalCuts.Sort();
// Insert the right bound h and w
// in their respective vectors
horizontalCuts.Add(h);
verticalCuts.Add(w);
int maxHorizontal = 0;
int maxVertical = 0;
// Find the maximum Horizontal Length possible
for(int i = 1; i < horizontalCuts.Count; i++)
{
int diff = horizontalCuts[i] - horizontalCuts[i - 1];
maxHorizontal = Math.Max(maxHorizontal, diff);
}
// Find the maximum vertical Length possible
for(int i = 1; i < verticalCuts.Count; i++)
{
int diff = verticalCuts[i] - verticalCuts[i - 1];
maxVertical = Math.Max(maxVertical, diff);
}
// Return the maximum area of rectangle
return (int)(maxHorizontal * maxVertical % mod);
}
static void Main ()
{
// Given Input
List<int> hc = new List<int>(new int[]{ 2, 5 });
List<int> vc = new List<int>(new int[]{ 1, 3 });
// Function Call
Console.WriteLine(maxArea(6, 4, hc, vc));
}
}
// This code is contributed by suresh07.
Javascript
<script>
// JavaScript program for the above approach
const mod = 1e9 + 7;
class Solution {
// Returns the maximum area of rectangle
// after Horizontal and Vertical Cuts
maxArea(h, w, horizontalCuts, verticalCuts) {
// Sort the two arrays
horizontalCuts.sort(function (a, b) { return a - b; })
verticalCuts.sort(function (a, b) { return a - b; })
// Insert the right bound h and w
// in their respective vectors
horizontalCuts.push(h);
verticalCuts.push(w);
let maxHorizontal = 0;
let maxVertical = 0;
// Find the maximum Horizontal Length possible
for (let i = 1; i < horizontalCuts.length; i++) {
let diff
= horizontalCuts[i] - horizontalCuts[i - 1];
maxHorizontal = Math.max(maxHorizontal, diff);
}
// Find the maximum vertical Length possible
for (let i = 1; i < verticalCuts.length; i++) {
let diff
= verticalCuts[i] - verticalCuts[i - 1];
maxVertical = Math.max(maxVertical, diff);
}
// Return the maximum area of rectangle
return parseInt(maxHorizontal * maxVertical
% mod);
}
}
// Driver Code
// Class Call
let ob = new Solution();
// Given Input
let hc = [2, 5], vc = [1, 3];
let h = 6, v = 4;
// Function Call
document.write(ob.maxArea(6, 4, hc, vc));
// This code is contributed by Potta Lokesh
</script>
6
Complejidad temporal: O(NlogN)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por nityavedanta3 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA