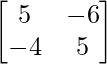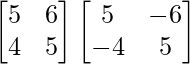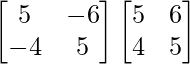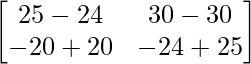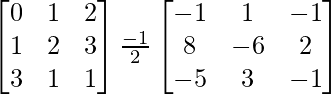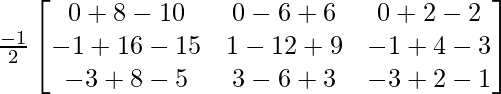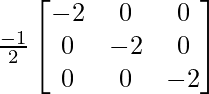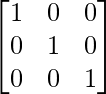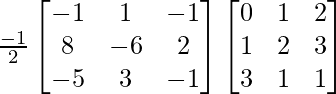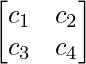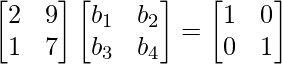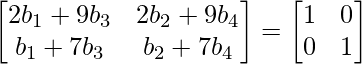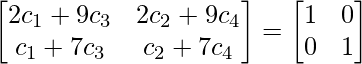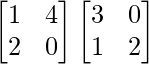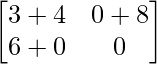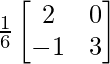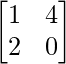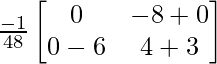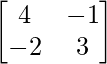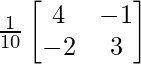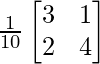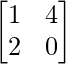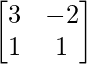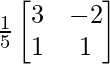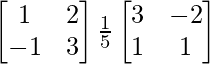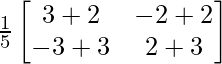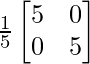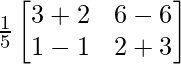Arrays Invertibles – Barcelona Geeks

Una array es una representación de elementos, en forma de arreglo rectangular. Una array consta de filas y columnas. Las líneas horizontales se conocen como filas y las líneas verticales se conocen como columnas. El orden de una array se define como número de filas × número de columnas. Si el número de filas en una array es «m» y el número de columnas es «n», entonces el orden de la array se representa como «m × n».

La inversa de una array

Supongamos que ‘A’ es una array cuadrada, ahora esta array ‘A’ se conoce como solo en una condición si existe otra array ‘B’ de la misma dimensión, tal que, AB = BA = I _n donde I _n se conoce como array identidad del mismo orden y la array ‘B’ se conoce como la inversa de la array ‘A’. La inversa de una array se puede representar como A ^-1 . También se conoce como

Por ejemplo:

un = $\begin{bmatrix} 5 &6 \\ 4&5 \end{bmatrix}$

y B = $\begin{bmatrix} 5 &-6 \\ -4&5 \end{bmatrix}$

Al multiplicar A y B se obtiene,

AB = $\begin{bmatrix} 5 &6 \\ 4&5 \end{bmatrix} \begin{bmatrix} 5&-6 \\ -4&5 \end{bmatrix}$

AB = $\begin{bmatrix} 25-24 &-30+30 \\ 20-20&-24+25 \end{bmatrix}$

AB = $\begin{bmatrix}1 &0 \\ 0&1 \end{bmatrix}$

AB = Yo ………. (1)

De manera similar, puede obtener BA multiplicando la array B y la array A.

AB = $\begin{bmatrix} 5 &-6 \\ -4&5 \end{bmatrix} \begin{bmatrix} 5 &6 \\ 4&5 \end{bmatrix}$

AB = $\begin{bmatrix} 25-24 &30-30 \\ -20+20&-24+25 \end{bmatrix}$

AB = $\begin{bmatrix} 1 &0 \\ 0&1 \end{bmatrix}$

BA = Yo………… (2)

De (1) y (2), puedes ver que AB = BA = I _n

Por lo tanto, A es una array invertible y la inversa de la array A es la array B. Esto se puede escribir como A ^-1 = B.

Si B es la array inversa de A, entonces también A es la array inversa de B. Entonces, puedes escribir B ^-1 = A.

Nota: La condición necesaria y suficiente para que una array cuadrada A posea la inversa es que la array no sea singular. Una array se llama array singular, si el determinante de la array es cero, es decir, |A| = 0. Entonces |A| ≠ 0 para una array A que es invertible.

Aplicación de array invertible:

La aplicación de la array invertible es:

Mínimos cuadrados o regresión
Simulaciones
Comunicaciones inalámbricas MIMO

Métodos de inversión de arrays:

Usando los siguientes métodos, puede encontrar la otra array, digamos la array ‘B’, que es la inversa de la array ‘A’:

Eliminación gaussiana
Método de Newton
Método Cayley-Hamilton
Método de descomposición de Eigen

Ejemplo: Comprobar si la array A= 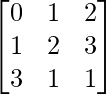$\begin{bmatrix} 0 &1 &2 \\ 1&2 &3 \\ 3& 1 & 1 \end{bmatrix}$ es invertible o no. Y si A es invertible, compruebe si la array B = 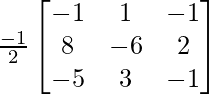$\frac{-1}{2}\begin{bmatrix} -1 &1 &-1 \\ 8&-6 &2 \\ -5& 3 & -1 \end{bmatrix}$ es inversa de la array A o no.

Solución:

Primero comprobamos si la array A es invertible o no.

|A| = 0×(2-3) – 1×(1-2) + 3×(3-4)

|A| = 0+1-3

|A| = -2 ≠0

Por eso. la array A es invertible.

Ahora, comprueba si AB=BA=I _n o no

AB = $\begin{bmatrix} 0 &1 &2 \\ 1&2 &3 \\ 3& 1 & 1 \end{bmatrix}\frac{-1}{2}\begin{bmatrix} -1 &1 &-1 \\ 8&-6 &2 \\ -5& 3 & -1 \end{bmatrix}$

AB = $\frac{-1}{2} \begin{bmatrix} 0 &1 &2\\ 1&2 &3 \\ 3& 1& 1 \end{bmatrix} \begin{bmatrix} -1 &1 &-1 \\ 8&-6 &2 \\ -5& 3 & -1 \end{bmatrix}$

AB = $\frac{-1}{2}\begin{bmatrix} 0+8-10 &0-6+6 &0+2-2 \\ -1+16-15&1-12+9 &-1+4-3 \\ -3+8-5& 3-6+3 & -3+2-1 \end{bmatrix}$

AB = $\frac{-1}{2} \begin{bmatrix} -2&0 &0\\ 0&-2 &0 \\ 0& 0& -2 \end{bmatrix}$

AB = $\begin{bmatrix} 1&0 &0\\ 0&1 &0 \\ 0& 0& 1 \end{bmatrix}$

AB = yo

AB = $\frac{-1}{2}\begin{bmatrix} -1 &1 &-1 \\ 8&-6 &2 \\ -5& 3 & -1 \end{bmatrix} \begin{bmatrix} 0 &1 &2 \\ 1&2 &3 \\ 3& 1 & 1 \end{bmatrix}$

AB = $\frac{-1}{2}\begin{bmatrix} -1 &1 &-1 \\ 8&-6 &2 \\ -5& 3 & -1 \end{bmatrix} \begin{bmatrix} 0 &1 &2\\ 1&2 &3 \\ 3& 1& 1 \end{bmatrix}$

AB = $\frac{-1}{2}\begin{bmatrix} 0+1-3 &-1+2-1 &-2+3-1 \\ 0-6+6&8-12+2 &16-18+2 \\ 0+3-3& -5+6-1 & -10+9-1 \end{bmatrix}$

AB = $\frac{-1}{2} \begin{bmatrix} -2&0 &0\\ 0&-2 &0 \\ 0& 0& -2 \end{bmatrix}$

AB = $\begin{bmatrix} 1&0 &0\\ 0&1 &0 \\ 0& 0& 1 \end{bmatrix}$

BA = yo

Puedes ver, AB = BA = I

Por lo tanto, la array B es inversa de la array A.

Teoremas de la array invertible

Teorema 1: Toda array invertible posee una única inversa.

Prueba:

Sea ‘A’ una array invertible n×n.

Consideremos que B y C son dos inversas de A.

Entonces, AB = BA = I …….(1)

y AC = CA = I …….. (2)

De (1) tienes

C(AB) = C(yo _norte ) = C ……..(3)

De (2) tienes

(CA)B = yo _norte (B) = B ……. (4)

Ya que, C(AB) = (CA)B [Ley de Asociatividad]

Entonces, C = B

Por lo tanto, está probado.

Ejemplo:

Sean A = $\begin{bmatrix} 2 &9 \\ 1& 7 \end{bmatrix}$ , B = $\begin{bmatrix} b_{1} &b_{2} \\ b_{3}& b_{4} \end{bmatrix}$ y C = $\begin{bmatrix} c_{1} &c_{2} \\ c_{3}& c_{4} \end{bmatrix}$

Si ambas arrays B y C son inversas de la array A entonces,

AB = BA = yo y

CA = CA = yo

Tomando AB = I

$\begin{bmatrix} 2 &9 \\ 1& 7 \end{bmatrix} \begin{bmatrix} b_{1} &b_{2} \\ b_{3}& b_{4} \end{bmatrix} = \begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix}$

$\begin{bmatrix} 2b_{1}+9b_{3} &2b_{2}+9b_{4} \\ b_{1}+7b_{3}& b_{2}+7b_{4} \end{bmatrix} = \begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix}$

Desde arriba, obtienes 4 ecuaciones.

2 b1 + 9 b3 = 1 ………. (1)

b1 + 7 b3 = 0 …………….(2)

2 b2 + 9 b4 = 0 …………..(3)

b2 + 7 b4 = 1 ……………….(4)

después de resolver estas 4 ecuaciones, obtendrás

b1 = 7/5

b2 = -9/5

b3 = -1/5

b4 = 2/5

Entonces array B = $\begin{bmatrix} \frac{7}{5} &\frac{-9}{5} \\ \frac{-1}{5}& \frac{2}{5} \end{bmatrix}$ ………… (5)

Ahora, considere AC = I

$\begin{bmatrix} 2 &9 \\ 1& 7 \end{bmatrix} \begin{bmatrix} c_{1} &c_{2} \\ c_{3}& c_{4} \end{bmatrix} = \begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix}$

$\begin{bmatrix} 2c_{1}+9c_{3} &2c_{2}+9c_{4} \\ c_{1}+7c_{3}& c_{2}+7c_{4} \end{bmatrix} = \begin{bmatrix} 1 &0 \\ 0& 1 \end{bmatrix}$

Desde arriba, obtienes 4 ecuaciones.

2 b1 + 9 b3 = 1 ………. (6)

b1 + 7 b3 = 0 …………….(7)

2 b2 + 9 b4 = 0 …………..(8)

b2 + 7 b4 = 1 ……………….(9)

Después de resolver estas 4 ecuaciones, obtendrás

b1 = 7/5

b2 = -9/5

b3 = -1/5

b4 = 2/5

Entonces array B = $\begin{bmatrix} \frac{7}{5} &\frac{-9}{5} \\ \frac{-1}{5}& \frac{2}{5} \end{bmatrix}$ ………..(10)

De (9) y (10) puede ver que las arrays B y C son iguales.

Por lo tanto, se demuestra que toda array invertible posee inversa única.

Teorema 2: Si A, B son dos arrays no singulares de n filas, entonces AB también es no singular y (AB) ^-1 = B ^-1 A ^-1

Prueba:

|A| ≠0, |B| ≠0

Entonces, |AB| ≠0

Sea una array C = B ^-1 A ^-1

(AB)C = (AB)B ^-1 A ^-1

(AB)C = A(BB ^-1 )A ^-1

(AB)C = IA _n A ^-1

(AB)C = AA- ¹

(AB)C = yo _norte

C(AB) = B- ¹ A – ¹ (AB)

C(AB) = B ^-1 A ^-1 AB

C(AB) = B ^-1 B

C(AB) = yo _norte

Dado que (AB)C = C(AB) = I _n

Por lo tanto, C es inversa de (AB)

Entonces (AB) ^-1 = B ^-1 A ^-1

Ejemplo:

Sean A = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix}$ y B = $\begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

AB = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix} \begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

AB = $\begin{bmatrix} 3+4 &0+8 \\ 6+0& 0 \end{bmatrix}$

AB = $\begin{bmatrix} 7 &8 \\ 6& 0 \end{bmatrix}$

(AB) ^-1 = \frac{-1}{48}\begin{bmatrix} 0 &-8 \\ -6& 7 \end{bmatrix} ………. (1)

La inversa de una array se puede obtener mediante la fórmula dada

A ^-1 = adjunto de la array A/ |A|

B = $\begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

B – ¹ = $\frac{1}{6}\begin{bmatrix} 2 &0 \\ -1& 3 \end{bmatrix}$

un = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix}$

A – ¹ = $\frac{1}{-8}\begin{bmatrix} 0 &-4 \\ -2& 1 \end{bmatrix}$

B – ¹ A – ¹ = $\frac{1}{6}\begin{bmatrix} 2 &0 \\ -1& 3 \end{bmatrix} \frac{1}{-8}\begin{bmatrix} 0 &-4 \\ -2& 1 \end{bmatrix}$

B – ¹ A – ¹ = $\frac{-1}{48}\begin{bmatrix} 0 &-8+0 \\ 0-6& 4+3 \end{bmatrix}$

B ^-1 A ^-1 = $\frac{-1}{48}\begin{bmatrix} 0 &-8 \\ -6& 7 \end{bmatrix}$ …….. (2)

De (1) y (2), puedes ver que (AB) ^-1 = B ^-1 A ^-1

Por lo tanto, se demuestra que (AB) ^-1 = B ^-1 A ^-1

Propiedades de la inversa de una array cuadrada

1. (A ^-1 ) ^-1 = A

Prueba:

Si A es una array invertible entonces

AA – ¹ = yo

Tomando inversa en ambos lados

(AA ^-1 ) ^-1 = I ^-1

(A ^-1 ) ^-1 A ^-1 = I [del teorema 2 (AB) ^-1 = B ^-1 A ^-1 ]

Multiplicando por A en ambos lados

(A ^-1 ) ^-1 A ^-1 A = IA

(A ^-1 ) ^-1 I = A

(A ^-1 ) ^-1 = A

Por lo tanto, se prueba que (A ^-1 ) ^-1 = A

Ejemplo:

Sea A = $\begin{bmatrix} 3 &1 \\ 2 & 4 \end{bmatrix}$

|A| = 12 – 2 = 10

adj A = $\begin{bmatrix} 4 &-1 \\ -2 & 3 \end{bmatrix}$

A ^-1 = adj A /|A|

A – ¹ = $\frac{1}{10}\begin{bmatrix} 4 &-1 \\ -2 & 3 \end{bmatrix}$

(A ^-1 ) ^-1 = adj (A ^-1 ) / |A ^-1 |

adj(A ^-1 ) = $\frac{1}{10}\begin{bmatrix} 3 &1 \\ 2 & 4 \end{bmatrix}$

|A ^-1 | = (12 – 10)/100

|A ^-1 | = 1/10

(A ^-1 ) ^-1 = $10*\frac{1}{10}\begin{bmatrix} 3 &1 \\ 2 & 4 \end{bmatrix}$

(A ^-1 ) ^-1 = $\begin{bmatrix} 3 &1 \\ 2 & 4 \end{bmatrix}$

Desde arriba puedes ver que (A ^-1 ) ^-1 = A

2. (A ₁ A ₂ A ₃ ………..A _n ) ^-1 = A _n^-1 A _n-1^-1 ……….A ₂^-1 A ₁^-1

También puedes escribirlo:

(AB) ^-1 = A ^-1 B ^-1

(ABC) ^-1 = A ^-1 B ^-1 C ^-1

Prueba:

Esto se puede demostrar por inducción matemática.

para n = 2

(A ₁ A ₂ ) ^-1 = A ₂^-1 A ₁^-1 ……….(1)

Esta declaración es verdadera. [por el teorema 2]

Sea esto cierto para n = k

(A ₁ A ₂ A ₃ ……….A _k ) ^-1 = A _k^-1 …………A ₂^-1 A ₁^-1 ……..(2)

Para n = k+1, tienes que probar esto.

(A ₁ A ₂ A ₃ ……….A _k A _k+1 ) ^-1

=((A ₁ A ₂ A ₃ ………A _k )A _k+1 ) ^-1

=((A _k^-1 …………A ₂^-1 A ₁^-1 )A _k+1 ) ^-1

=(A _k+1 ) ^-1 (A _k^-1 …………A ₂^-1 A ₁^-1 ) [usando el teorema 2]

= Ak ₊₁^-1_Ak^-1 ………….A ₂^-1 A ₁^-1

Por lo tanto, está probado.

Ejemplo:

Supongamos que hay dos arrays A y B,

Sea A = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix}$

y B = $\begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

AB = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix} \begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

AB = $\begin{bmatrix} 3+4 &0+8 \\ 6+0& 0 \end{bmatrix}$

AB = $\begin{bmatrix} 7 &8 \\ 6& 0 \end{bmatrix}$

(AB) ^-1 = $\frac{-1}{48}\begin{bmatrix} 0 &-8 \\ -6& 7 \end{bmatrix}$ ………. (1)

La inversa de una array se puede obtener mediante la fórmula dada

A ^-1 = adjunto de la array A/ |A|

B = $\begin{bmatrix} 3 &0 \\ 1& 2 \end{bmatrix}$

B – ¹ = $\frac{1}{6}\begin{bmatrix} 2 &0 \\ -1& 3 \end{bmatrix}$

un = $\begin{bmatrix} 1 &4 \\ 2& 0 \end{bmatrix}$

A – ¹ = $\frac{1}{-8}\begin{bmatrix} 0 &-4 \\ -2& 1 \end{bmatrix}$

B – ¹ A – ¹ = $\frac{1}{6}\begin{bmatrix} 2 &0 \\ -1& 3 \end{bmatrix} \frac{1}{-8}\begin{bmatrix} 0 &-4 \\ -2& 1 \end{bmatrix}$

B – ¹ A – ¹ = $\frac{-1}{48}\begin{bmatrix} 0 &-8+0 \\ 0-6& 4+3 \end{bmatrix}$

B ^-1 A ^-1 = $\frac{-1}{48}\begin{bmatrix} 0 &-8 \\ -6& 7 \end{bmatrix}$ …….. (2)

De (1) y (2), puedes ver que (AB) ^-1 = B ^-1 A ^-1

Por lo tanto, se demuestra que (AB) ^-1 = B ^-1 A ^-1

3. AA ^-1 = A ^-1 A = Yo _norte

Prueba:

Una array es invertible si AA ^-1 = I

Multiplicar por A en ambos lados

AAA ^-1 = IA

IA = A

Multiplicando por A ^-1 en ambos lados

A ^-1 AI = A ^-1 A

yo = A ^-1 A

Por lo tanto, se prueba que AA ^-1 = I = A ^-1 A

Ejemplo:

Sea A = $\begin{bmatrix} 1 &2 \\ -1 &3 \end{bmatrix}$

|A| = 3 + 2 = 5

adj A = $\begin{bmatrix} 3 &-2 \\ 1 &1 \end{bmatrix}$

A ^-1 = adj A \|A|

A – ¹ = $\frac{1}{5}\begin{bmatrix} 3 &-2 \\ 1 &1 \end{bmatrix}$

Ahora para probar AA ^-1 = A ^-1 A = I

Tomando el lado izquierdo

AA ^-1

$\begin{bmatrix} 1 &2 \\ -1 &3 \end{bmatrix}\frac{1}{5}\begin{bmatrix} 3 &-2 \\ 1 &1 \end{bmatrix}$

$\frac{1}{5}\begin{bmatrix} 3 +2 &-2 +2\\ -3+3 &2+3 \end{bmatrix}$

$\frac{1}{5}\begin{bmatrix} 5 & 0\\ 0&5 \end{bmatrix}$

$\begin{bmatrix} 1 & 0\\ 0&1 \end{bmatrix}$

La array anterior es igual a la array identidad.

Ahora tomando el lado derecho

A ^-1 A

$\frac{1}{5} \begin{bmatrix} 3 &-2 \\ 1 &1 \end{bmatrix} \begin{bmatrix} 1 &2 \\ -1 &3 \end{bmatrix}$

$\frac{1}{5}\begin{bmatrix} 3+2 & 6-6\\ 1-1&2+3 \end{bmatrix}$

$\frac{1}{5}\begin{bmatrix} 5 & 0\\ 0&5 \end{bmatrix}$

$\begin{bmatrix} 1 & 0\\ 0&1 \end{bmatrix}$

La array anterior es igual a la array identidad.

Por lo tanto, se prueba que AA ^-1 = A ^-1 A = I