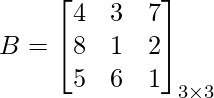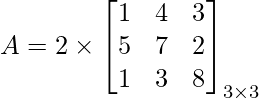Arrays y sus Tipos | Clase 12 Matemáticas

Una array de estructura rectangular con entradas se conoce como Matrix. Una array tiene uno o más de un número de filas y columnas. Cada entrada en la array puede contener números, letras, símbolos, etc. Las entradas en líneas horizontales se conocen como filas y las entradas en líneas verticales se conocen como columnas. Cada entrada pertenece a una fila y una columna. Una array está representada por [A] _m×n donde m es el número de filas y n es el número de columnas presentes en una array. y un elemento de la array se puede representar como un _ij donde i y j son la i-ésima fila y la j-ésima columna a la que pertenece un elemento. elementos donde i y j son iguales (es decir, el número de fila y el número de columna son iguales) se conoce como elemento diagonal. La array A se puede escribir como:

$\begin{bmatrix} a_{11}& a_{11} & a_{11} &. & . &. & a_{11}\\ a_{11} & a_{11} & a_{11} & . &. &. & a_{11} \\ a_{11}& a_{11} & a_{11} & . &. &. & a_{11} \\ .&. &. &. &. &. &. \\ . &. &. &. &. &. &. \\ . &. &. &. &. &. &. \\ . & . &. &. &. &. &. \\ a_{11}& a_{11} & a_{11} &. &. &. & a_{11} \end{bmatrix}_{m\times n}$

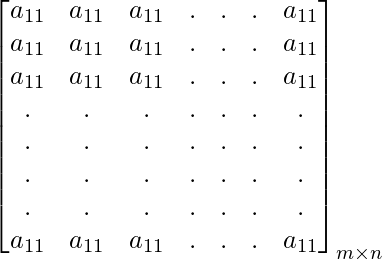
Ejemplo de una array

$\begin{bmatrix} 1& 5 &8 &5 \\ 3& 4 &0 & 12 \\ 7& 2 &3 & 10 \\ \end{bmatrix}_{3\times 4}$

Tipos de M atrix

Hay muchos tipos de array. Hablaremos uno por uno:

Array de filas

Una array que contiene solo una fila y cualquier número de columnas se conoce como array fila.

Ejemplo:

$\begin{bmatrix} 1& 3&7 \end{bmatrix}_{1\times 3}$

Array de columnas

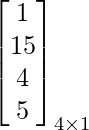
Una array que contiene solo una columna y cualquier número de filas se conoce como array columna.

Ejemplo:

$\begin{bmatrix} 1\\ 15 \\ 4\\ 5 \\ \end{bmatrix}_{4\times 1}$

Array Singleton

Una array que tiene un solo elemento se conoce como array singleton. En este tipo de array el número de columnas y el número de filas es igual a 1.

Ejemplo:

$\begin{bmatrix} 5 \end{bmatrix}_{1\times 1}$

array rectangular

Una array que no tiene el mismo número de filas y columnas se conoce como array rectangular. Una array rectangular se puede representar como [A] _m×n

Ejemplo:

$\begin{bmatrix} 1& 3 &7 &15 \\ 3& 4 &6 & 11 \\ 5& 2 &9 & 8 \\ \end{bmatrix}_{3\times 4}$

Array cuadrada

Una array que tiene el mismo número de filas y el mismo número de columnas se conoce como array cuadrada. Generalmente, la representación utilizada para la array cuadrada es [A] _n×n .

Ejemplo:

$\begin{bmatrix} 8& 3 &2 \\ 6& 4 &6 \\ 5& 7 &9 \\ \end{bmatrix}_{3\times 3}$

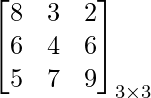
array nula

Una array que tiene todos los elementos como 0 se conoce como array nula.

Ejemplo:

$\begin{bmatrix} 0& 0 &0 \\ 0& 0 &0 \\ 0& 0 &0 \\ \end{bmatrix}_{3\times 3}$

Array diagonal

Una array que tiene todos los elementos como 0 excepto los elementos diagonales se conoce como array diagonal.

Ejemplo:

$\begin{bmatrix} 8& 0 &0 \\ 0& 4 &0 \\ 0& 0 &9 \\ \end{bmatrix}_{3\times 3}$

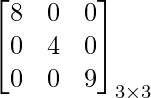
array escalar

Una array que tiene todos los elementos como 0 excepto los elementos diagonales y todos los elementos diagonales son iguales se conoce como array escalar. Es una especie de array diagonal donde todos los elementos diagonales son iguales.

Ejemplo:

$\begin{bmatrix} 4& 0 &0 \\ 0& 4 &0 \\ 0& 0 &4 \\ \end{bmatrix}_{3\times 3}$

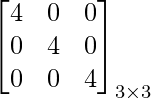
Array de identidad

Es una especie de array escalar donde todos los elementos diagonales son 1 y todos los elementos no diagonales son 0. La array identidad siempre tiene el mismo número de filas y columnas.

Ejemplo:

$\begin{bmatrix} 1& 0 &0 \\ 0& 1 &0 \\ 0& 0 &1 \\ \end{bmatrix}_{3\times 3}$

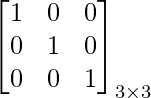
Array triangular superior

Esta array es una especie de array cuadrada que tiene todos los elementos como 0 debajo de la diagonal.

Ejemplo:

$\begin{bmatrix} 8& 5 &6 \\ 0& 4 &7 \\ 0& 0 &9 \\ \end{bmatrix}_{3\times 3}$

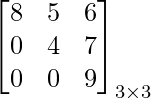
Array triangular inferior

Esta array es una especie de array cuadrada en la que todos los elementos por encima de la diagonal son 0.

Ejemplo:

$\begin{bmatrix} 8& 0 &0 \\ 6& 4 &0 \\ 5& 7 &9 \\ \end{bmatrix}_{3\times 3}$

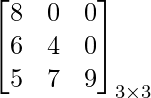
Rastro de una array

La suma de los elementos de la diagonal de una array se conoce como la traza de una array. La traza de una array A se puede representar como tr(A). La traza de una array se puede calcular solo para una array cuadrada.

Ejemplo:

$A= \begin{bmatrix} 15& 12 &9 \\ 4& 6 &11 \\ 5& 9 &0 \\ \end{bmatrix}_{3\times 3}$

tr(A) = 15 + 6 + 0 = 21

Propiedades de una traza de array

i) La traza de la suma de dos arrays es igual a la suma de la traza de la array individual.

Explicación:

Matemáticamente se puede escribir como tr(A+B) = tr(A) + tr(B)

$A= \begin{bmatrix} 15& 12 &9 \\ 4& 6 &11 \\ 5& 9 &0 \\ \end{bmatrix}_{3\times 3}$

tr(A) = 15 + 6 + 0 = 21

$B= \begin{bmatrix} 4& 3 &7 \\ 8& 1 &2 \\ 5& 6 &1 \\ \end{bmatrix}_{3\times 3}$

tr(B) = 4 + 1 + 1 = 6

Ahora, tr(A)+tr(B) = 21+6 = 27

$A+B= \begin{bmatrix} 19& 15&16 \\ 12& 7 &13 \\ 10& 15 &1 \\ \end{bmatrix}_{3\times 3}$

tr(A + B) = 19 + 7 + 1 = 27

Puedes ver, tr(A) + tr(B) = tr(A + tr(B)

Del mismo modo, tr(A – B) = tr(A) – tr(B)

ii) La traza de una array que se multiplica por algún escalar es igual a la multiplicación de la traza de la array y el escalar.

Explicación:

Matemáticamente se puede representar como tr(kA) = k tr(A)

$A=2\times \begin{bmatrix} 1& 4 &3 \\ 5& 7 &2 \\ 1& 3 &8 \\ \end{bmatrix}_{3\times 3}$

tr(2 × A) = 2 + 14 + 16 = 32

$2\times A= \begin{bmatrix} 2& 8 &6 \\ 10& 14 &4 \\ 2& 6 &16 \\ \end{bmatrix}_{3\times 3}$

2 × tr(A) = 2 * (1 + 7 + 8)

= 32

Puedes ver tr(2 × A) = 2 × tr(A)

Publicación traducida automáticamente

Artículo escrito por ntptiwari y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ejemplo de una array

Tipos de M atrix

Array de filas

Array de columnas

Array Singleton

array rectangular

Array cuadrada

array nula

Array diagonal

array escalar

Array de identidad

Array triangular superior

Array triangular inferior

Rastro de una array

Propiedades de una traza de array

Deja una respuesta Cancelar la respuesta