Borde máximo ponderado en la ruta entre dos Nodes en un árbol N-ario usando elevación binaria

Posted on by Rudeus Greyrat

Dado un árbol N-ario con borde ponderado y consultas Q donde cada consulta contiene dos Nodes del árbol. La tarea es encontrar el borde ponderado máximo en el camino simple entre estos dos Nodes.
Ejemplos: 
 

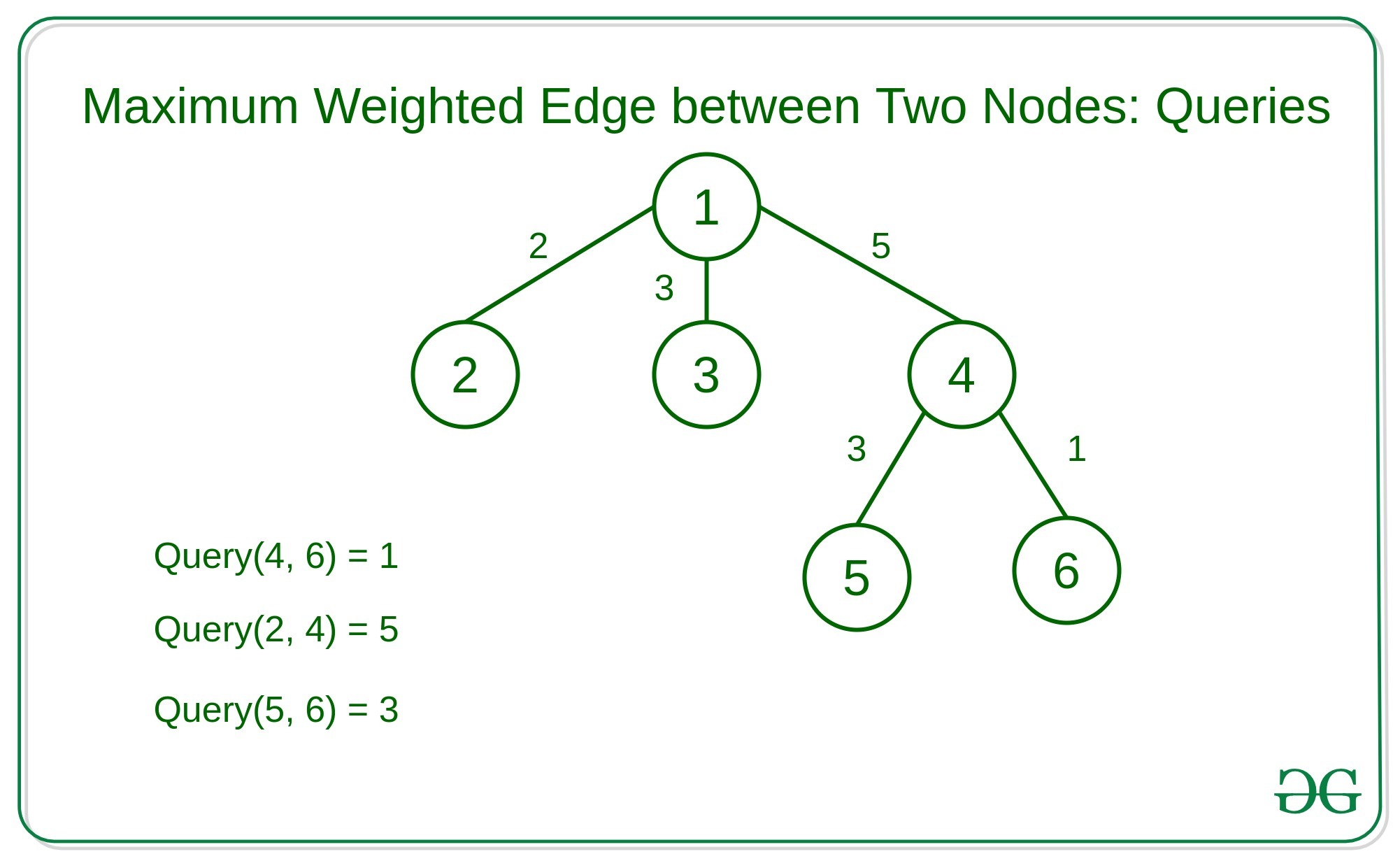
Enfoque ingenuo: una solución simple es recorrer todo el árbol para cada consulta y encontrar la ruta entre los dos Nodes.
Enfoque eficiente: la idea es utilizar la elevación binaria para precalcular el borde ponderado máximo de cada Node a todos los demás Nodes a una distancia de algunos 

2^{i}

. Guardaremos el borde ponderado máximo hasta 
2^{i}

nivel. 

dp[i][j] = dp[i - 1][dp[i - 1][j]]  

y 

mx[i][j] = max(mx[i - 1][j], mx[i - 1][dp[i - 1][j]])

dónde 

  • j es el Node y
  • yo es la distancia de

2^{i}

  • dp[i][j] almacena el padre de j en

2^{i}

  • distancia si está presente, de lo contrario almacenará 0
  • mx[i][j] almacena el borde máximo del Node j al padre de este Node en

2^{i}

  • distancia.

Haremos una búsqueda profunda para encontrar a todos los padres en 
2^{0}

distancia y su peso y luego precalcular los padres y los bordes máximos en cada 
2^{i}

distancia.
A continuación se muestra la implementación del enfoque anterior:

C++

// C++ implementation to find the
// maximum weighted edge in the simple
// path between two nodes in N-ary Tree
 
#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 100005;
 
// Depths of Nodes
vector<int> level(N);
const int LG = 20;
 
// Parent at every 2^i level
vector<vector<int> > dp(LG, vector<int>(N));
 
// Maximum node at every 2^i level
vector<vector<int> > mx(LG, vector<int>(N));
 
// Graph that stores destinations
// and its weight
vector<vector<pair<int, int> > > v(N);
int n;
 
// Function to traverse the nodes
// using the Depth-First Search Traversal
void dfs_lca(int a, int par, int lev)
{
    dp[0][a] = par;
    level[a] = lev;
    for (auto i : v[a]) {
 
        // Condition to check if its
        // equal to its parent then skip
        if (i.first == par)
            continue;
        mx[0][i.first] = i.second;
 
        // DFS Recursive Call
        dfs_lca(i.first, a, lev + 1);
    }
}
 
// Function to find the ancestor
void find_ancestor()
{
 
    // Loop to set every 2^i distance
    for (int i = 1; i < LG; i++) {
        // Loop to calculate for
        // each node in the N-ary tree
        for (int j = 1; j <= n; j++) {
            dp[i][j]
                = dp[i - 1][dp[i - 1][j]];
 
            // Storing maximum edge
            mx[i][j]
                = max(mx[i - 1][j],
                      mx[i - 1][dp[i - 1][j]]);
        }
    }
}
 
int getMax(int a, int b)
{
    // Swaping if node a is at more depth
    // than node b because we will
    // always take at more depth
    if (level[b] < level[a])
        swap(a, b);
 
    int ans = 0;
 
    // Difference between the depth of
    // the two given nodes
    int diff = level[b] - level[a];
    while (diff > 0) {
        int log = log2(diff);
        ans = max(ans, mx[log][b]);
 
        // Changing Node B to its
        // parent at 2 ^ i distance
        b = dp[log][b];
 
        // Subtracting distance by 2^i
        diff -= (1 << log);
    }
 
    // Take both a, b to its
    // lca and find maximum
    while (a != b) {
        int i = log2(level[a]);
 
        // Loop to find the 2^ith
        // parent that is different
        // for both a and b i.e below the lca
        while (i > 0
               && dp[i][a] == dp[i][b])
            i--;
 
        // Updating ans
        ans = max(ans, mx[i][a]);
        ans = max(ans, mx[i][b]);
 
        // Changing value to its parent
        a = dp[i][a];
        b = dp[i][b];
    }
    return ans;
}
 
// Function to compute the Least
// common Ancestor
void compute_lca()
{
    dfs_lca(1, 0, 0);
    find_ancestor();
}
 
// Driver Code
int main()
{
    // Undirected tree
    n = 5;
    v[1].push_back(make_pair(2, 2));
    v[2].push_back(make_pair(1, 2));
    v[1].push_back(make_pair(3, 5));
    v[3].push_back(make_pair(1, 5));
    v[3].push_back(make_pair(4, 3));
    v[4].push_back(make_pair(3, 4));
    v[3].push_back(make_pair(5, 1));
    v[5].push_back(make_pair(3, 1));
 
    // Computing LCA
    compute_lca();
 
    int queries[][2]
        = { { 3, 5 },
            { 2, 3 },
            { 2, 4 } };
    int q = 3;
 
    for (int i = 0; i < q; i++) {
        int max_edge = getMax(queries[i][0],
                              queries[i][1]);
        cout << max_edge << endl;
    }
    return 0;
}

Java

// Java implementation to find the
// maximum weighted edge in the simple
// path between two nodes in N-ary Tree
import java.util.*;
import java.awt.Point;
public class Main
{
    static int N = 100005;
     
    // Depths of Nodes
    static int[] level = new int[N];
    static int LG = 20;
   
    // Parent at every 2^i level
    static int[][] dp = new int[LG][N];
   
    // Maximum node at every 2^i level
    static int[][] mx = new int[LG][N];
   
    // Graph that stores destinations
    // and its weight
    static Vector<Vector<Point>> v = new Vector<Vector<Point>>();
      
    static int n = 0;
   
    // Function to traverse the
    // nodes using the Depth-First
    // Search Traversal
    static void dfs_lca(int a, int par, int lev)
    {
        dp[0][a] = par;
        level[a] = lev;
        for(int i = 0; i < v.get(a).size(); i++)
        {
            // Condition to check
            // if its equal to its
            // parent then skip
            if (v.get(a).get(i).x == par)
                continue;
            mx[0][v.get(a).get(i).x] = v.get(a).get(i).y;
   
            // DFS Recursive Call
            dfs_lca(v.get(a).get(i).x, a, lev + 1);
        }
    }
   
    // Function to find the ancestor
    static void find_ancestor()
    {
        // Loop to set every 2^i distance
        for(int i = 1; i < 16; i++)
        {
            // Loop to calculate for
            // each node in the N-ary tree
            for(int j = 1; j < n + 1; j++)
            {
                dp[i][j] = dp[i - 1][dp[i - 1][j]];
   
                // Storing maximum edge
                mx[i][j] = Math.max(mx[i - 1][j], mx[i - 1][dp[i - 1][j]]);
            }
        }
    }
   
    static int getMax(int a, int b)
    {
        // Swaping if node a is at more depth
        // than node b because we will
        // always take at more depth
        if (level[b] < level[a])
        {
            int temp = a;
            a = b;
            b = temp;
        }
   
        int ans = 0;
   
        // Difference between the
        // depth of the two given
        // nodes
        int diff = level[b] - level[a];
   
        while (diff > 0)
        {
            int log = (int)(Math.log(diff) / Math.log(2));
            ans = Math.max(ans, mx[log][b]);
   
            // Changing Node B to its
            // parent at 2 ^ i distance
            b = dp[log][b];
   
            // Subtracting distance by 2^i
            diff -= (1 << log);
        }
   
        // Take both a, b to its
        // lca and find maximum
        while (a != b)
        {
            int i = (int)(Math.log(level[a]) / Math.log(2));
   
            // Loop to find the maximum 2^ith
            // parent the is different
            // for both a and b
            while (i > 0 && dp[i][a] == dp[i][b])
            {
                i-=1;
            }
   
            // Updating ans
            ans = Math.max(ans, mx[i][a]);
            ans = Math.max(ans, mx[i][b]);
   
            // Changing value to
            // its parent
            a = dp[i][a];
            b = dp[i][b];
        }
   
        return ans;
    }
   
    // Function to compute the Least
    // common Ancestor
    static void compute_lca()
    {
        dfs_lca(1, 0, 0);
        find_ancestor();
    }
     
    public static void main(String[] args) {
        for(int i = 0; i < LG; i++)
        {
            for(int j = 0; j < N; j++)
            {
                dp[i][j] = 0;
                mx[i][j] = 0;
            }
        }
          
        for(int i = 0; i < N; i++)
        {
            v.add(new Vector<Point>());
        }
          
        // Undirected tree
        v.get(1).add(new Point(2, 2));
        v.get(2).add(new Point(1, 2));
        v.get(1).add(new Point(3, 5));
        v.get(3).add(new Point(1, 5));
        v.get(3).add(new Point(4, 3));
        v.get(4).add(new Point(3, 4));
        v.get(3).add(new Point(5, 1));
        v.get(5).add(new Point(3, 1));
       
        // Computing LCA
        compute_lca();
       
        int[][] queries
            = { { 3, 5 },
                { 2, 3 },
                { 2, 4 } };
        int q = 3;
       
        for (int i = 0; i < q; i++) {
            int max_edge = getMax(queries[i][0],
                                  queries[i][1]);
            System.out.println(max_edge);
        }
    }
}
 
// This code is contributed by decode2207.

Python3

# Python3 implementation to
# find the maximum weighted
# edge in the simple path
# between two nodes in N-ary Tree
import math
N = 100005;
  
# Depths of Nodes
level = [0 for i in range(N)]
LG = 20;
  
# Parent at every 2^i level
dp = [[0 for j in range(N)]
         for i in range(LG)]
  
# Maximum node at every 2^i level
mx = [[0 for j in range(N)]
         for i in range(LG)]
  
# Graph that stores destinations
# and its weight
v = [[] for i in range(N)]
n = 0
  
# Function to traverse the
# nodes using the Depth-First
# Search Traversal
def dfs_lca(a, par, lev):
 
    dp[0][a] = par;
    level[a] = lev;
     
    for i in v[a]:
  
        # Condition to check
        # if its equal to its
        # parent then skip
        if (i[0] == par):
            continue;
        mx[0][i[0]] = i[1];
  
        # DFS Recursive Call
        dfs_lca(i[0], a, lev + 1);
 
# Function to find the ancestor
def find_ancestor():
  
    # Loop to set every 2^i distance
    for i in range(1, 16):
     
        # Loop to calculate for
        # each node in the N-ary tree
        for j in range(1, n + 1):
         
            dp[i][j] = dp[i - 1][dp[i - 1][j]];
  
            # Storing maximum edge
            mx[i][j] = max(mx[i - 1][j],
                           mx[i - 1][dp[i - 1][j]]);
 
def getMax(a, b):
 
    # Swaping if node a is at more depth
    # than node b because we will
    # always take at more depth
    if (level[b] < level[a]):
        a, b = b, a
  
    ans = 0;
  
    # Difference between the
    # depth of the two given
    # nodes
    diff = level[b] - level[a];
     
    while (diff > 0):
        log = int(math.log2(diff));
        ans = max(ans, mx[log][b]);
  
        # Changing Node B to its
        # parent at 2 ^ i distance
        b = dp[log][b];
  
        # Subtracting distance by 2^i
        diff -= (1 << log);
      
    # Take both a, b to its
    # lca and find maximum
    while (a != b):
        i = int(math.log2(level[a]));
  
        # Loop to find the maximum 2^ith
        # parent the is different
        # for both a and b
        while (i > 0 and
               dp[i][a] == dp[i][b]):
            i-=1
  
        # Updating ans
        ans = max(ans, mx[i][a]);
        ans = max(ans, mx[i][b]);
  
        # Changing value to
        # its parent
        a = dp[i][a];
        b = dp[i][b];
     
    return ans;
  
# Function to compute the Least
# common Ancestor
def compute_lca():
     
    dfs_lca(1, 0, 0);
    find_ancestor();
 
# Driver code
if __name__=="__main__":
     
    # Undirected tree
    n = 5;
    v[1].append([2, 2]);
    v[2].append([1, 2]);
    v[1].append([3, 5]);
    v[3].append([1, 5]);
    v[3].append([4, 3]);
    v[4].append([3, 4]);
    v[3].append([5, 1]);
    v[5].append([3, 1]);
  
    # Computing LCA
    compute_lca();
  
    queries= [[3, 5], [2, 3], [2,4]]
    q = 3;
     
    for i in range(q):
        max_edge = getMax(queries[i][0],
                          queries[i][1]);
        print(max_edge)
         
# This code is contributed by Rutvik_56

C#

// C# implementation to find the
// maximum weighted edge in the simple
// path between two nodes in N-ary Tree
using System;
using System.Collections.Generic;
class GFG {
     
    static int N = 100005;
    
    // Depths of Nodes
    static int[] level = new int[N];
    static int LG = 20;
  
    // Parent at every 2^i level
    static int[,] dp = new int[LG, N];
  
    // Maximum node at every 2^i level
    static int[,] mx = new int[LG, N];
  
    // Graph that stores destinations
    // and its weight
    static List<List<Tuple<int,int>>> v = new List<List<Tuple<int,int>>>();
     
    static int n = 0;
  
    // Function to traverse the
    // nodes using the Depth-First
    // Search Traversal
    static void dfs_lca(int a, int par, int lev)
    {
        dp[0,a] = par;
        level[a] = lev;
        for(int i = 0; i < v[a].Count; i++)
        {
            // Condition to check
            // if its equal to its
            // parent then skip
            if (v[a][i].Item1 == par)
                continue;
            mx[0,v[a][i].Item1] = v[a][i].Item2;
  
            // DFS Recursive Call
            dfs_lca(v[a][i].Item1, a, lev + 1);
        }
    }
  
    // Function to find the ancestor
    static void find_ancestor()
    {
        // Loop to set every 2^i distance
        for(int i = 1; i < 16; i++)
        {
            // Loop to calculate for
            // each node in the N-ary tree
            for(int j = 1; j < n + 1; j++)
            {
                dp[i,j] = dp[i - 1,dp[i - 1,j]];
  
                // Storing maximum edge
                mx[i,j] = Math.Max(mx[i - 1,j], mx[i - 1,dp[i - 1,j]]);
            }
        }
    }
  
    static int getMax(int a, int b)
    {
        // Swaping if node a is at more depth
        // than node b because we will
        // always take at more depth
        if (level[b] < level[a])
        {
            int temp = a;
            a = b;
            b = temp;
        }
  
        int ans = 0;
  
        // Difference between the
        // depth of the two given
        // nodes
        int diff = level[b] - level[a];
  
        while (diff > 0)
        {
            int log = (int)(Math.Log(diff) / Math.Log(2));
            ans = Math.Max(ans, mx[log,b]);
  
            // Changing Node B to its
            // parent at 2 ^ i distance
            b = dp[log,b];
  
            // Subtracting distance by 2^i
            diff -= (1 << log);
        }
  
        // Take both a, b to its
        // lca and find maximum
        while (a != b)
        {
            int i = (int)(Math.Log(level[a]) / Math.Log(2));
  
            // Loop to find the maximum 2^ith
            // parent the is different
            // for both a and b
            while (i > 0 && dp[i,a] == dp[i,b])
            {
                i-=1;
            }
  
            // Updating ans
            ans = Math.Max(ans, mx[i,a]);
            ans = Math.Max(ans, mx[i,b]);
  
            // Changing value to
            // its parent
            a = dp[i,a];
            b = dp[i,b];
        }
  
        return ans;
    }
  
    // Function to compute the Least
    // common Ancestor
    static void compute_lca()
    {
        dfs_lca(1, 0, 0);
        find_ancestor();
    }
 
  static void Main() {
       
    for(int i = 0; i < LG; i++)
    {
        for(int j = 0; j < N; j++)
        {
            dp[i,j] = 0;
            mx[i,j] = 0;
        }
    }
     
    for(int i = 0; i < N; i++)
    {
        v.Add(new List<Tuple<int,int>>());
    }
     
    // Undirected tree
    v[1].Add(new Tuple<int,int>(2, 2));
    v[2].Add(new Tuple<int,int>(1, 2));
    v[1].Add(new Tuple<int,int>(3, 5));
    v[3].Add(new Tuple<int,int>(1, 5));
    v[3].Add(new Tuple<int,int>(4, 3));
    v[4].Add(new Tuple<int,int>(3, 4));
    v[3].Add(new Tuple<int,int>(5, 1));
    v[5].Add(new Tuple<int,int>(3, 1));
  
    // Computing LCA
    compute_lca();
  
    int[,] queries
        = { { 3, 5 },
            { 2, 3 },
            { 2, 4 } };
    int q = 3;
  
    for (int i = 0; i < q; i++) {
        int max_edge = getMax(queries[i,0],
                              queries[i,1]);
        Console.WriteLine(max_edge);
    }
  }
}
 
// This code is contributed by divyesh072019.

Javascript

<script>
    // Javascript implementation to find the
    // maximum weighted edge in the simple
    // path between two nodes in N-ary Tree
     
    let N = 100005;
   
    // Depths of Nodes
    let level = new Array(N);
    level.fill(0);
    let LG = 20;
 
    // Parent at every 2^i level
    let dp = new Array(LG);
    for(let i = 0; i < LG; i++)
    {
        dp[i] = new Array(N);
        for(let j = 0; j < N; j++)
        {
            dp[i][j] = 0;
        }
    }
 
    // Maximum node at every 2^i level
    let mx = new Array(LG);
    for(let i = 0; i < LG; i++)
    {
        mx[i] = new Array(N);
        for(let j = 0; j < N; j++)
        {
            mx[i][j] = 0;
        }
    }
 
    // Graph that stores destinations
    // and its weight
    let v = [];
    for(let i = 0; i < N; i++)
    {
        v.push([]);
    }
    let n = 0;
 
    // Function to traverse the
    // nodes using the Depth-First
    // Search Traversal
    function dfs_lca(a, par, lev)
    {
        dp[0][a] = par;
        level[a] = lev;
        for(let i = 0; i < 2; i++)
        {
            // Condition to check
            // if its equal to its
            // parent then skip
            if (v[a][0] == par)
                continue;
            mx[0][v[a][0]] = v[a][1];
 
            // DFS Recursive Call
            dfs_lca(v[a][0], a, lev + 1);
        }
    }
 
    // Function to find the ancestor
    function find_ancestor()
    {
        // Loop to set every 2^i distance
        for(let i = 1; i < 16; i++)
        {
            // Loop to calculate for
            // each node in the N-ary tree
            for(let j = 1; j < n + 1; j++)
            {
                dp[i][j] = dp[i - 1][dp[i - 1][j]];
 
                // Storing maximum edge
                mx[i][j] = Math.max(mx[i - 1][j], mx[i - 1][dp[i - 1][j]]);
            }
        }
    }
 
    function getMax(a, b)
    {
        // Swaping if node a is at more depth
        // than node b because we will
        // always take at more depth
        if (level[b] < level[a])
        {
            let temp = a;
            a = b;
            b = temp;
        }
 
        let ans = 0;
 
        // Difference between the
        // depth of the two given
        // nodes
        let diff = level[b] - level[a];
 
        while (diff > 0)
        {
            let log = parseInt(Math.log(diff) / Math.log(2), 10);
            ans = Math.max(ans, mx[log][b]);
 
            // Changing Node B to its
            // parent at 2 ^ i distance
            b = dp[log][b];
 
            // Subtracting distance by 2^i
            diff -= (1 << log);
        }
 
        // Take both a, b to its
        // lca and find maximum
        while (a == b)
        {
            i = parseInt(Math.log(level[a]) / Math.log(2), 10);
 
            // Loop to find the maximum 2^ith
            // parent the is different
            // for both a and b
            while (i > 0 && dp[i][a] == dp[i][b])
            {
                i-=1;
            }
 
            // Updating ans
            ans = Math.max(ans, mx[i][a]);
            ans = Math.max(ans, mx[i][b]);
 
            // Changing value to
            // its parent
            a = dp[i][a];
            b = dp[i][b];
        }
 
        return ans*2 + 1;
    }
 
    // Function to compute the Least
    // common Ansector
    function compute_lca()
    {
        dfs_lca(1, 0, 0);
        find_ancestor();
    }
     
    // Undirected tree
    n = 5;
    v[1].push(2);
    v[1].push(2);
    v[2].push(1);
    v[2].push(2);
    v[1].push(3);
    v[1].push(5);
    v[3].push(1);
    v[3].push(5);
    v[3].push(4);
    v[3].push(3);
    v[4].push(3);
    v[4].push(4);
    v[3].push(5);
    v[3].push(1);
    v[5].push(3);
    v[5].push(1);
   
    // Computing LCA
    compute_lca();
   
    let queries= [[3, 5], [2, 3], [2,4]];
    let q = 3;
      
    for(let i = 0; i <q; i++)
    {
        let max_edge = getMax(queries[i][0],
                          queries[i][1]);
        document.write(max_edge + "</br>");
    }
 
// This code is contributed by suresh07.
</script>
Producción: 

1
5
5

 

Complejidad temporal: O(N*logN).
Espacio Auxiliar: O(N*logN).
 

Publicación traducida automáticamente

Artículo escrito por insiderpants y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *