La Inteligencia Artificial es el estudio de los agentes de construcción que actúan racionalmente. La mayoría de las veces, estos agentes realizan algún tipo de algoritmo de búsqueda en segundo plano para lograr sus tareas.
- Un problema de búsqueda consiste en:
- Un espacio de estado. Conjunto de todos los estados posibles en los que puedes estar.
- Un Estado de Inicio. El estado desde donde comienza la búsqueda.
- Una prueba de gol. Una función que analiza el estado actual devuelve si es o no el estado objetivo.
- La solución a un problema de búsqueda es una secuencia de acciones, denominada plan, que transforma el estado inicial en el estado objetivo.
- Este plan se logra a través de algoritmos de búsqueda.
Tipos de algoritmos de búsqueda:
Hay demasiados algoritmos de búsqueda poderosos para caber en un solo artículo. En cambio, este artículo discutirá seis de los algoritmos de búsqueda fundamentales, divididos en dos categorías, como se muestra a continuación.
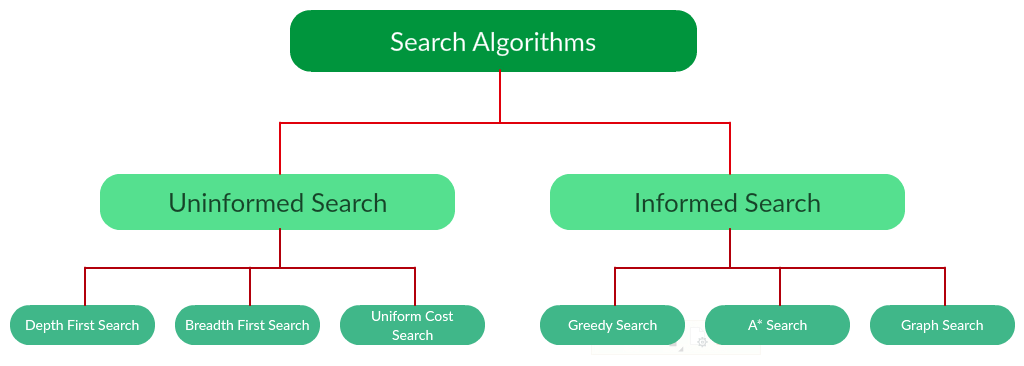
Tenga en cuenta que hay mucho más para buscar algoritmos que el gráfico que he proporcionado anteriormente. Sin embargo, este artículo se apegará principalmente a la tabla anterior, explorando los algoritmos que se dan allí.
Algoritmos de búsqueda no informados:
Los algoritmos de búsqueda de esta sección no tienen información adicional sobre el Node de destino además de la proporcionada en la definición del problema. Los planes para alcanzar el estado objetivo desde el estado inicial difieren solo por el orden y/o la duración de las acciones. La búsqueda desinformada también se llama búsqueda ciega . Estos algoritmos solo pueden generar los sucesores y diferenciar entre el estado objetivo y el estado no objetivo.
En esta sección se analizan los siguientes algoritmos de búsqueda no informada.
- Primera búsqueda en profundidad
- Búsqueda primero en amplitud
- Búsqueda de costos uniformes
Cada uno de estos algoritmos tendrá:
- Un gráfico de problema que contiene el Node de inicio S y el Node de destino G.
- Una estrategia, que describe la manera en que se recorrerá el gráfico para llegar a G.
- Una franja, que es una estructura de datos utilizada para almacenar todos los estados posibles (Nodes) a los que puede ir desde los estados actuales.
- Un árbol, que resulta al atravesar el Node de destino.
- Un plan de solución , que la secuencia de Nodes de S a G.
Primera búsqueda en profundidad :
La búsqueda en profundidad (DFS) es un algoritmo para atravesar o buscar estructuras de datos de árboles o gráficos. El algoritmo comienza en el Node raíz (seleccionando algún Node arbitrario como Node raíz en el caso de un gráfico) y explora lo más lejos posible a lo largo de cada rama antes de retroceder. Utiliza la estrategia de último en entrar, primero en salir y, por lo tanto, se implementa utilizando una pila.
Ejemplo:
Pregunta. ¿Qué solución encontraría DFS para pasar del Node S al Node G si se ejecuta en el siguiente gráfico?
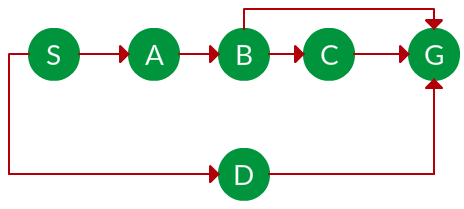
Solución. El árbol de búsqueda equivalente para el gráfico anterior es el siguiente. A medida que DFS atraviesa el árbol «primero el Node más profundo», siempre elegiría la rama más profunda hasta llegar a la solución (o se queda sin Nodes y pasa a la siguiente rama). El recorrido se muestra con flechas azules.
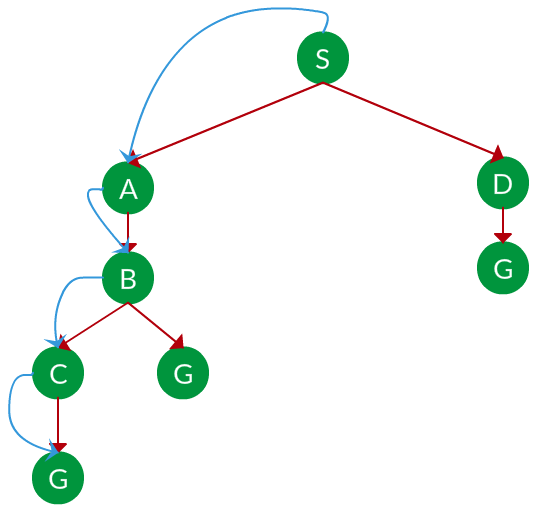
Ruta: S -> A -> B -> C -> G
= la profundidad del árbol de búsqueda = el número de niveles del árbol de búsqueda.
= número de Nodes en el nivel
.
Complejidad temporal: Equivalente al número de Nodes atravesados en DFS.
Complejidad del espacio: equivalente a qué tan grande puede llegar a ser la franja.
Integridad: DFS está completo si el árbol de búsqueda es finito, lo que significa que para un árbol de búsqueda finito dado, DFS encontrará una solución si existe.
Optimalidad: DFS no es óptimo, lo que significa que la cantidad de pasos para llegar a la solución o el costo gastado para alcanzarla es alto.
Primera búsqueda en amplitud :
La búsqueda en amplitud (BFS) es un algoritmo para atravesar o buscar estructuras de datos de árboles o gráficos. Comienza en la raíz del árbol (o algún Node arbitrario de un gráfico, a veces denominado «clave de búsqueda») y explora todos los Nodes vecinos en la profundidad actual antes de pasar a los Nodes en el siguiente nivel de profundidad. Se implementa mediante una cola.
Ejemplo:
Pregunta. ¿Qué solución encontraría BFS para pasar del Node S al Node G si se ejecuta en el siguiente gráfico?

Solución. El árbol de búsqueda equivalente para el gráfico anterior es el siguiente. A medida que BFS atraviesa el árbol «primero el Node más superficial», siempre elegiría la rama menos profunda hasta llegar a la solución (o se queda sin Nodes y pasa a la siguiente rama). El recorrido se muestra con flechas azules.
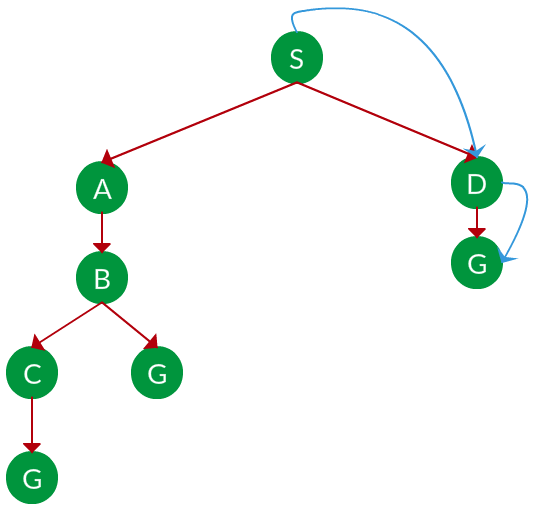
Ruta: S -> D -> G
= la profundidad de la solución menos profunda.
= número de Nodes en el nivel
.
Complejidad temporal: Equivalente al número de Nodes atravesados en BFS hasta la solución más superficial.
Complejidad del espacio: equivalente a qué tan grande puede llegar a ser la franja.
Completitud: BFS está completo, lo que significa que para un árbol de búsqueda determinado, BFS encontrará una solución, si existe.Optimalidad: BFS es óptimo siempre que los costos de todos los bordes sean iguales.
Búsqueda de costos uniformes:
UCS es diferente de BFS y DFS porque aquí entran en juego los costos. En otras palabras, atravesar diferentes bordes podría no tener el mismo costo. El objetivo es encontrar un camino donde la suma acumulada de costos sea la menor.
El costo de un Node se define como:
cost(node) = cumulative cost of all nodes from root cost(root) = 0
Ejemplo:
Pregunta. ¿Qué solución encontraría UCS para pasar del Node S al Node G si se ejecuta en el siguiente gráfico?
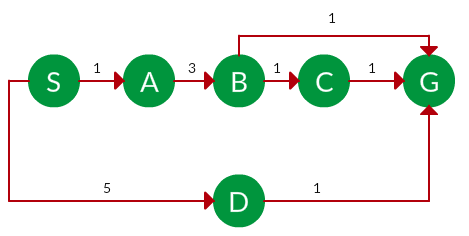
Solución. El árbol de búsqueda equivalente para el gráfico anterior es el siguiente. El costo de cada Node es el costo acumulado de llegar a ese Node desde la raíz. Con base en la estrategia UCS, se elige la ruta con el menor costo acumulativo. Tenga en cuenta que debido a las muchas opciones en el margen, el algoritmo explora la mayoría de ellas siempre que su costo sea bajo y las descarta cuando encuentra una ruta de menor costo; estos recorridos descartados no se muestran a continuación. El recorrido real se muestra en azul.
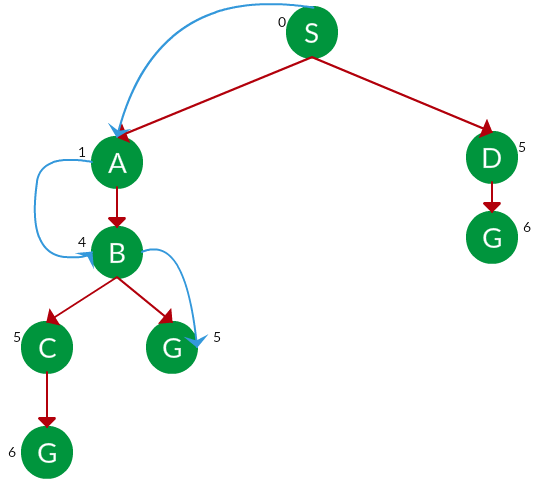
Ruta: S -> A -> B -> G
Costo: 5Let
= costo de la solución.
= coste de los arcos.
Entonces
la profundidad efectiva
Complejidad temporal:
, Complejidad espacial:
ventajas:
- UCS está completo solo si los estados son finitos y no debe haber un ciclo con peso cero.
- UCS es óptimo solo si no hay un costo negativo.
Desventajas:
- Explora opciones en cada “dirección”.
- No hay información sobre la ubicación de la meta.
Algoritmos de búsqueda informados:
Aquí, los algoritmos tienen información sobre el estado del objetivo, lo que ayuda a una búsqueda más eficiente. Esta información se obtiene mediante algo llamado heurística.
En esta sección, discutiremos los siguientes algoritmos de búsqueda.
- Búsqueda codiciosa
- A* Árbol de búsqueda
- A* Búsqueda de gráficos
Heurística de búsqueda: en una búsqueda informada, una heurística es una función que estima qué tan cerca está un estado del estado objetivo. Por ejemplo: distancia de Manhattan, distancia euclidiana, etc. (A menor distancia, más cerca de la meta). Se utilizan diferentes heurísticas en diferentes algoritmos informados que se analizan a continuación.
Búsqueda codiciosa:
En la búsqueda codiciosa, expandimos el Node más cercano al Node objetivo. La “cercanía” se estima mediante una heurística h(x).
Heurística: Una heurística h se define como-
h(x) = Estimación de la distancia del Node x desde el Node objetivo.
Baje el valor de h(x), más cerca está el Node de la meta.
Estrategia: Expandir el Node más cercano al estado objetivo, es decir , expandir el Node con un valor h más bajo.
Ejemplo:
Pregunta. Encuentra el camino de S a G usando la búsqueda codiciosa. Los valores heurísticos h de cada Node debajo del nombre del Node.
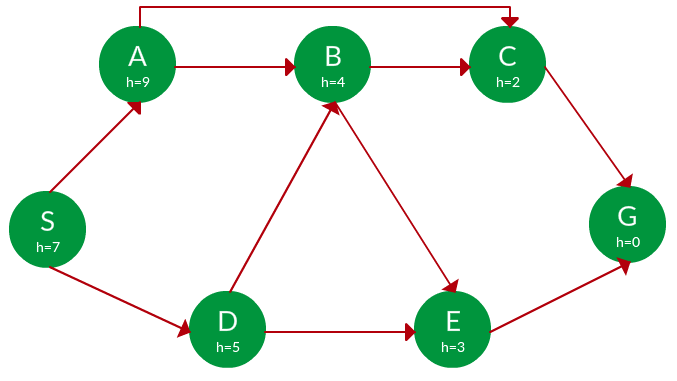
Solución. Partiendo de S, podemos atravesar A(h=9) o D(h=5). Elegimos D, ya que tiene el menor costo heurístico. Ahora desde D, podemos pasar a B(h=4) o E(h=3). Elegimos E con un costo heurístico más bajo. Finalmente, de E, vamos a G(h=0). Este recorrido completo se muestra en el árbol de búsqueda a continuación, en azul.
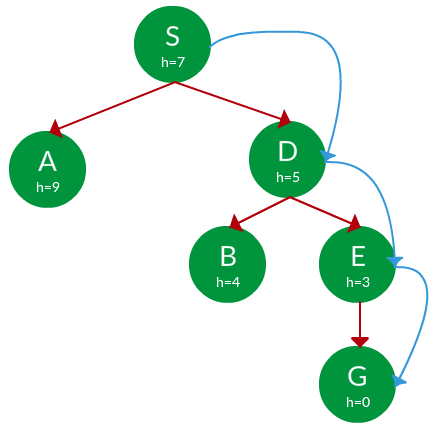
Ruta: S -> D -> E -> G
Ventaja: funciona bien con problemas de búsqueda informados, con menos pasos para alcanzar un objetivo.
Desventaja: puede convertirse en DFS no guiado en el peor de los casos.
A* Árbol de búsqueda:
A* Tree Search, o simplemente conocido como A* Search, combina las fortalezas de la búsqueda de costo uniforme y la búsqueda codiciosa. En esta búsqueda, la heurística es la suma del costo en UCS, denotado por g(x), y el costo en la búsqueda codiciosa, denotado por h(x). El costo total se denota por f(x).
Heurística: Los siguientes puntos deben tenerse en cuenta con la heurística en la búsqueda A*. ![]()
- Aquí, h(x) se denomina costo directo y es una estimación de la distancia del Node actual desde el Node objetivo.
- Y, g(x) se denomina costo hacia atrás y es el costo acumulativo de un Node desde el Node raíz.
- Una búsqueda* es óptima solo cuando, para todos los Nodes, el costo directo de un Node h(x) subestima el costo real h*(x) para alcanzar la meta. Esta propiedad de la heurística A* se llama admisibilidad .
Estrategia: elija el Node con el valor f(x) más bajo.
Ejemplo:
Pregunta. Encuentre la ruta para llegar de S a G usando la búsqueda A*.
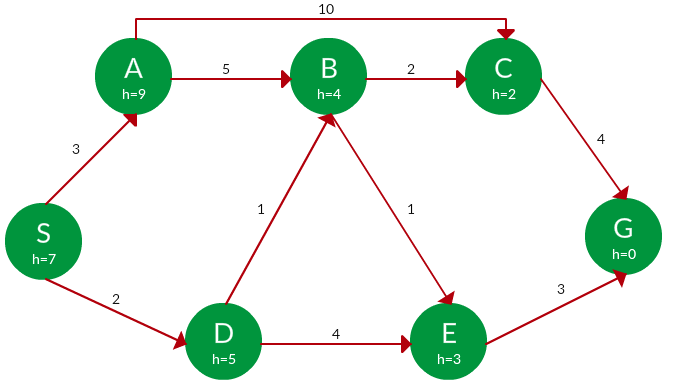
Solución. A partir de S, el algoritmo calcula g(x) + h(x) para todos los Nodes en la franja en cada paso, eligiendo el Node con la suma más baja. El trabajo completo se muestra en la siguiente tabla.
Tenga en cuenta que en el cuarto conjunto de iteraciones, obtenemos dos caminos con el mismo costo sumado f(x), por lo que los expandimos en el siguiente conjunto. El camino con un costo más bajo en una mayor expansión es el camino elegido.
| Sendero | h(x) | g(x) | f(x) |
|---|---|---|---|
| S | 7 | 0 | 7 |
| S->A | 9 | 3 | 12 |
| S -> D ✔ | 5 | 2 | 7 |
| S -> D -> B ✔ | 4 | 2 + 1 = 3 | 7 |
| S->D->E | 3 | 2 + 4 = 6 | 9 |
| S -> D -> B -> C ✔ | 2 | 3 + 2 = 5 | 7 |
| S -> D -> B -> E ✔ | 3 | 3 + 1 = 4 | 7 |
| S -> D -> B -> C -> G | 0 | 5 + 4 = 9 | 9 |
| S -> D -> B -> E -> G ✔ | 0 | 4 + 3 = 7 | 7 |
Costo: 7
A* Búsqueda de gráfico :
- La búsqueda de árbol A* funciona bien, excepto que lleva tiempo volver a explorar las ramas que ya ha explorado. En otras palabras, si el mismo Node se ha expandido dos veces en diferentes ramas del árbol de búsqueda, la búsqueda A* podría explorar ambas ramas, perdiendo así el tiempo.
- A* Graph Search, o simplemente Graph Search, elimina esta limitación al agregar esta regla: no expanda el mismo Node más de una vez.
- Heurístico. La búsqueda de gráficos es óptima solo cuando el costo directo entre dos Nodes sucesivos A y B, dado por h(A) – h (B), es menor o igual que el costo hacia atrás entre esos dos Nodes g(A -> B). Esta propiedad de la heurística de búsqueda de grafos se llama consistencia .
Ejemplo:
Pregunta. Use búsquedas de gráficos para encontrar rutas de S a G en el siguiente gráfico.

la solución. Resolvemos esta pregunta más o menos de la misma manera que resolvimos la última pregunta, pero en este caso, mantenemos un registro de los Nodes explorados para no volver a explorarlos.
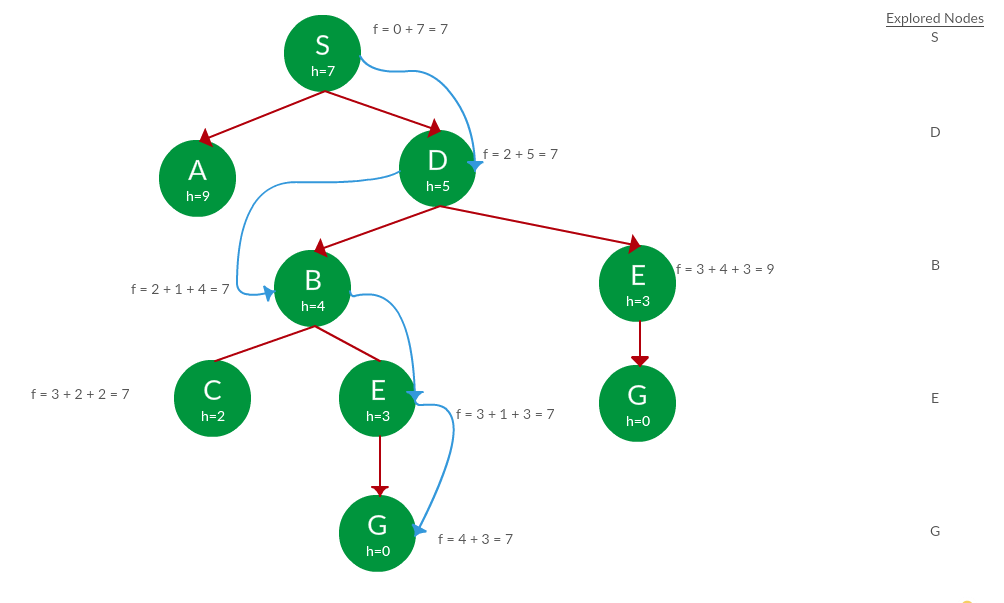
Ruta: S -> D -> B -> C -> E -> G
Costo: 7
Publicación traducida automáticamente
Artículo escrito por MdRafiAkhtar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
