Cálculo de integrales definidas

Las integrales son una parte muy importante del cálculo. Nos permiten calcular las antiderivadas, es decir, dada la derivada de una función, las integrales dan como resultado la función. Otras aplicaciones importantes de las integrales incluyen el cálculo del área bajo la curva, el volumen encerrado por una superficie, etc. Mientras que la aplicación anterior involucra principalmente integrales indefinidas, la última requiere que los límites estén bien definidos y la integral se calcula entre esos límites solamente. Tales integrales se llaman integrales definidas.

Integrales definidas

Las integrales definidas se utilizan principalmente para calcular las áreas y los volúmenes encerrados por las curvas. Por lo general, el área se calcula usando fórmulas bien definidas para rectángulos, círculos y cuadrados, etc. En la vida real, las formas no son tan simples, por lo tanto, para calcular las áreas de cualquier forma arbitraria, usamos las integrales definidas. Para una función f(x) definida en el intervalo [a, b], la integral definida entre estos límites viene dada por,

$\int^{b}_af(x)dx$

Aquí a se llama el límite inferior de la función y b se llama el límite superior de la función.

Dada una función f(x) que es continua en el intervalo [a, b], dividimos el intervalo en n subintervalos de igual ancho, $\Delta x$ y de cada intervalo elegimos un punto $x^{*}_{i}$ . Entonces la integral definida de f(x) de a a b es,

$\int^{b}_{a}f(x)dx = \lim_{n \to \infty}\sum^{n}_{i = 1}f(x_{i}^{*})\Delta x$

La figura anterior explica la definición del límite, a medida que aumentamos el número de rectángulos debajo de la curva, el área aproximada se vuelve más y más cercana al área real debajo de la figura.

Teorema fundamental del cálculo

El área de la región delimitada por la curva f(x) entre las ordenadas x = a y x = b y el eje x viene dada por $\int^{b}_{a}f(x)dx$ . Digamos que x es cualquier punto entre los límites, entonces $\int^{x}_{a}f(x)dx$ representa el área de la región desde a hasta x. En otras palabras, el área de esta región sombreada desde «a» hasta el valor x se llama función de área. está dado por,

$A = \int^{x}_{a}f(x)dx$

Con base en esta definición, se definen dos teoremas fundamentales del cálculo.

Primer Teorema Fundamental del Cálculo

Sea f(x) una función continua en el intervalo cerrado [a, b] y sea A(x) la función de área.

Entonces, A'(x) = f(x), para todo x ∈ [a, b].

Segundo Teorema Fundamental del Cálculo

Sea f(x) una función continua en el intervalo cerrado [a, b] y sean F(x) las antiderivadas de la función f(x). Después,

$\int^{b}_{a}f(x)dx = [F(x)]^{b}_{a} = F(b) - F(a)$

Área bajo la curva

El área bajo la curva viene dada por las integrales definidas. Sabemos que el área siempre es una cantidad positiva, pero al usar las integrales definidas, a veces el área que sale es negativa. Por ejemplo, considere las dos funciones a continuación, una se encuentra completamente por encima del eje x, la otra tiene una parte que se encuentra por debajo del eje x. En tales casos, las dos áreas podrían anularse entre sí.

En este caso, el área está dada por,

$A = \int^{b}_{a}f(x)dx$

Para este caso, las áreas negativa y positiva se deben calcular por separado y solo se debe sumar la magnitud de sus áreas.

$A = \int^{c}_{a}f(x)dx + \int^{b}_{c}f(x)dx$

Integrales definidas de funciones racionales

Para calcular las integrales definidas para tales funciones, estas funciones se descomponen mediante manipulación algebraica.

Pregunta: Calcula el valor de la siguiente integral

$\int^{3}_{1}\frac{1 - x}{x^2}dx$

Solución:

$\int^{3}_{1}\frac{1 - x}{x^2}dx \\ = \int^{3}_{1}( \frac{1}{x^2} - \frac{1}{x})dx \\ = \int^{3}_{1}( \frac{1}{x^2} )dx- \int^{3}_{1}(\frac{1}{x})dx \\ = [\frac{-1}{x}]^3_1 - [log(x)]^{3}_{1} \\ = 1 - \frac{1}{3} - (log(3) - log(1)) \\ = \frac{2}{3} - log(3)$

Integrales definidas de funciones radicales

Para calcular las integrales definidas de tales funciones, usamos la regla de la potencia inversa.

Pregunta: Calcula el valor de la siguiente integral

$\int^{1}_{0}x^{\frac{1}{3}}dx$

Solución:

$\int^{1}_{0}x^{\frac{1}{3}}dx$

Usando la regla de la potencia inversa,

$\int^{1}_{0}x^{\frac{1}{3}}dx \\ = [\frac{x^{\frac{4}{3}}}{\frac{3}{4}}]^{1}_{0} \\ = \frac{4}{3}$

Integrales definidas de funciones trigonométricas

Para calcular las integrales definidas de tales funciones, usamos la regla de la potencia inversa.

Pregunta: Calcula el valor de la siguiente integral

$\int^{1}_{0}sin(x)dx$

Solución:

$\int^{1}_{0}sin(x)dx \\ = [-cos(x)]^{1}_{0} \\ = 1 - cos(1)$

Integrales definidas de la función logarítmica natural

Para calcular las integrales definidas para tales funciones, usamos la siguiente identidad.

$\int ln(x)dx = xln(x) - x + C$

Pregunta: Calcula el valor de la siguiente integral

$\int^{2}_{1}(ln(x) + 1)dx$

Solución:

$\int^{2}_{1}(ln(x) + 1)dx \\ = \int^{2}_{1} ln(x)dx + \int^{2}_{1} 1dx$

Usando la fórmula mencionada anteriormente,

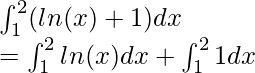
$\int^{2}_{1} ln(x)dx + \int^{2}_{1} 1dx \\ = [xln(x) - x]^2_1 + [x]^2_1 \\ = ((2ln(2) - 2) - (1ln(1) - 1)) + (2 - 1) \\ = (2ln(2) - 1) + 1\\ = 2ln(2)$

Veamos algunos problemas de muestra.

Problemas de muestra

Pregunta 1: Calcula el valor de la siguiente integral

$\int^{3}_{1}(x^2 + x)dx$

Solución:

$\int^{3}_{1}(x^2 + x)dx \\ = \int^{3}_{1}x^2dx + \int^{3}_{1}xdx \\ = [\frac{x^3}{3}]^3_1 + [\frac{x^2}{2}]^3_1 \\ = 9 - \frac{1}{3} + \frac{9}{2} - \frac{1}{2} \\ = 12 - \frac{1}{3} \\ = \frac{35}{3}$

Pregunta 2: Calcula el valor de la siguiente integral

$\int^{1}_{0}\frac{(x^2 + x)}{x}dx$

Solución:

$\int^{1}_{0}\frac{(x^2 + x)}{x}dx \\ = \int^{1}_{0}xdx + \int^{1}_{0}1dx \\ = [\frac{x^2}{2}]^1_0 + [x]^{1}_{0} \\ = \frac{1}{2} + 1 \\ = \frac{3}{2}$

Pregunta 3: Calcula el valor de la siguiente integral

$\int^{1}_{0}(\sqrt{x} + x)dx$

Solución:

$\int^{1}_{0}(\sqrt{x} + x)dx$

Usando la regla de la potencia inversa

$\int^{1}_{0}(\sqrt{x} + x)dx \\ =[\frac{x^{\frac{3}{2}}}{\frac{3}{2}} + x^2]^1_0 \\ = [\frac{2x^{\frac{3}{2}}}{3} + x^2]^1_0 \\ = \frac{2}{3} + 1 \\ = \frac{5}{3}$

Pregunta 4: Calcula el valor de la siguiente integral

$\int^{1}_{0}sin(x) + cos(x)dx$

Solución:

$\int^{1}_{0}sin(x) + cos(x)dx \\ = [-cos(x) + sin(x)]^1_0 \\ = [-cos(1) + sin(1)] - [1] \\ = sin(1) - cos(1) - 1$

Pregunta 5: Calcula el valor de la siguiente integral

$\int^{2}_{1}(ln(x) + e^x)dx$

Solución:

$\int^{2}_{1}(ln(x) + e^x)dx \\ = \int^{2}_{1} ln(x)dx + \int^{2}_{1} e^xdx$

Usando la fórmula mencionada anteriormente,

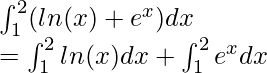
$\int^{2}_{1} ln(x)dx + \int^{2}_{1} e^xdx \\ = [xln(x) - x]^2_1 + [e^x]^2_1 \\ = ((2ln(2) - 2) - (1ln(1) - 1)) + (e^2 - e) \\ = (2ln(2) - 1) + e^2 - e\\ = 2ln(2) + e^2 -e -1$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Integrales definidas

Teorema fundamental del cálculo

Área bajo la curva

Problemas de muestra

Deja una respuesta Cancelar la respuesta