Cálculo de n-ésima raíz real usando búsqueda binaria

Dados dos números x y n, encuentra la raíz enésima de x. 

Ejemplos: 

Entrada: 5 2
Salida: 2.2360679768025875

Entrada:  x = 5, n = 3
Salida: 1.70997594668

Para calcular la raíz ^enésima de un número, podemos usar el siguiente procedimiento.  

1. Si x se encuentra en el rango [0, 1), entonces establecemos el límite inferior bajo = x y el límite superior alto = 1 , porque para este rango de números, la raíz n-ésima siempre es mayor que el número dado y nunca puede exceder 1.
   p . –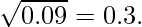 
2. De lo contrario, tomamos bajo = 1 y alto = x .
3. Declare una variable llamada epsilon e inicialícela para obtener la precisión que necesita. 
   Digamos epsilon=0.01, entonces podemos garantizar que nuestra estimación de la raíz enésima del número dado será 
   correcta hasta 2 decimales.
4. Declare una estimación variable e inicialícela para adivinar = (bajo + alto)/2.
5. Ejecuta un bucle tal que: 
   • si el error absoluto de nuestra conjetura es mayor que épsilon , haga lo siguiente: 
     1. si adivinar ⁿ > x , entonces alto = adivinar
     2. más bajo = adivinar
     3. Hacer una nueva y mejor conjetura , es decir, conjetura=(bajo+alto)/2.
   • Si el error absoluto de nuestra conjetura es menor que épsilon, salga del ciclo.

Error absoluto: el error absoluto se puede calcular como abs (adivinar ⁿ -x) 

// C++ Program to find
// n-th real root of x
#include <bits/stdc++.h>
using namespace std;
 
void findNthRoot(double x, int n)
{
 
    // Initialize boundary values
    double low, high;
    if (x >= 0 and x <= 1)
    {
        low = x;
        high = 1;
    }
    else
    {
        low = 1;
        high = x;
    }
 
    // Used for taking approximations
    // of the answer
    double epsilon = 0.00000001;
 
    // Do binary search
    double guess = (low + high) / 2;
    while (abs((pow(guess, n)) - x) >= epsilon)
    {
        if (pow(guess, n) > x)
        {
            high = guess;
        }
        else
        {
            low = guess;
        }
        guess = (low + high) / 2;
    }
 
    cout << fixed << setprecision(16) << guess;
}
 
// Driver code
int main()
{
    double x = 5;
    int n = 2;
    findNthRoot(x, n);
}
 
// This code is contributed
// by Subhadeep

// Java Program to find n-th real root of x
class GFG
{
    static void findNthRoot(double x, int n)
    {
 
        // Initialize boundary values
        double low, high;
        if (x >= 0 && x <= 1)
        {
            low = x;
            high = 1;
        }
        else
        {
            low = 1;
            high = x;
        }
 
        // used for taking approximations
        // of the answer
        double epsilon = 0.00000001;
 
        // Do binary search
        double guess = (low + high) / 2;
        while (Math.abs((Math.pow(guess, n)) - x)
               >= epsilon)
        {
            if (Math.pow(guess, n) > x)
            {
                high = guess;
            }
            else
            {
                low = guess;
            }
            guess = (low + high) / 2;
        }
 
        System.out.println(guess);
    }
 
    // Driver code
    public static void main(String[] args)
    {
        double x = 5;
        int n = 2;
        findNthRoot(x, n);
    }
}
 
// This code is contributed
// by mits

# Python Program to find n-th real root
# of x
 
 
def findNthRoot(x, n):
 
    # Initialize boundary values
    x = float(x)
    n = int(n)
    if (x >= 0 and x <= 1):
        low = x
        high = 1
    else:
        low = 1
        high = x
 
    # used for taking approximations
    # of the answer
    epsilon = 0.00000001
 
    # Do binary search
    guess = (low + high) / 2
    while abs(guess ** n - x) >= epsilon:
        if guess ** n > x:
            high = guess
        else:
            low = guess
        guess = (low + high) / 2
    print(guess)
 
 
# Driver code
x = 5
n = 2
findNthRoot(x, n)

// C# Program to find n-th real root of x
 
using System;
 
public class GFG {
    static void findNthRoot(double x, int n)
    {
 
        // Initialize boundary values
        double low, high;
        if (x >= 0 && x <= 1)
        {
            low = x;
            high = 1;
        }
        else
        {
            low = 1;
            high = x;
        }
 
        // used for taking approximations
        // of the answer
        double epsilon = 0.00000001;
 
        // Do binary search
        double guess = (low + high) / 2;
        while (Math.Abs((Math.Pow(guess, n)) - x)
               >= epsilon)
        {
            if (Math.Pow(guess, n) > x)
            {
                high = guess;
            }
            else
            {
                low = guess;
            }
            guess = (low + high) / 2;
        }
 
        Console.WriteLine(guess);
    }
 
    // Driver code
    static public void Main()
    {
        double x = 5;
        int n = 2;
        findNthRoot(x, n);
    }
}
 
// This code is contributed by akt_mit

<script>
 
    // Javascript Program to find n-th
    // real root of x
     
    function findNthRoot(x, n)
    {
  
        // Initialize boundary values
        let low, high;
        if (x >= 0 && x <= 1)
        {
            low = x;
            high = 1;
        }
        else
        {
            low = 1;
            high = x;
        }
  
        // used for taking approximations
        // of the answer
        let epsilon = 0.00000001;
  
        // Do binary search
        let guess = parseInt((low + high) / 2, 10);
        while (Math.abs((Math.pow(guess, n)) - x)
                >= epsilon)
        {
            if (Math.pow(guess, n) > x)
            {
                high = guess;
            }
            else
            {
                low = guess;
            }
            guess = (low + high) / 2;
        }
  
        document.write(guess);
    }
     
    let x = 5;
    let n = 2;
    findNthRoot(x, n);
     
</script>

2.2360679768025875

Complejidad de tiempo : O (log (x * 10 ^d ) * log _conjetura (n))

Espacio Auxiliar: O(1)

Aquí d es el número de lugares decimales hasta el cual queremos el resultado con precisión.

Explicación del primer ejemplo con epsilon = 0.01

Since taking too small value of epsilon as taken in our program might not be feasible for
explanation because it will increase the number of steps drastically so for the sake of
simplicity we are taking epsilon = 0.01
The above procedure will work as follows:
Say we have to calculate the then x = 5, low = 1, high = 5.Taking epsilon = 0.01First Guess:guess = (1 + 5) / 2 = 3Absolute error = |32 - 5| = 4 > epsilonguess2 = 9 > 5(x) then high = guess --> high = 3Second Guess:guess = (1 + 3) / 2 = 2Absolute error = |22 - 5| = 1 > epsilonguess2 = 4 > 5(x) then low = guess --> low = 2Third Guess:guess = (2 + 3) / 2 = 2.5Absolute error = |2.52 - 5| = 1.25 > epsilonguess2 = 6.25 > 5(x) then high = guess --> high = 2.5and proceeding so on we will get the  correct up to 2 decimal places i.e.,  = 2.23600456We will ignore the digits after 2 decimal places since they may or may not be correct.