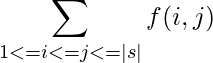Calcule la suma de la proporción de caracteres especiales a la longitud de las substrings de la string dada

Posted on by Rudeus Greyrat

Dada una string str y una array de caracteres especiales, specialArray[] , la tarea es encontrar la suma de la relación entre el recuento de caracteres especiales y la longitud de la substring para todas las posibles substrings de la string dada.

La relación entre el recuento de caracteres especiales en una substring y la longitud de las substrings de la string dada viene dada por 

f(i, j) = \frac{\displaystyle\sum_{k = i}^{j} special(s_k)}{j - i + 1}
 
La suma de las proporciones calculadas anteriormente viene dada por 
 
\displaystyle\sum_{1<=i<=j<=|s|}^{} f(i, j)

Ejemplos: 

Entrada: str = “abcdabc”, specialArray[] = {‘a’, ‘b’, ‘c’, ‘d’} 
Salida: 28.00000 
Explicación: 
Longitud de la string = 7 
Recuento de todas las substrings posibles = (7 * (8 + 1)) / 2 = 28 
Dado que todos los caracteres de la string están incluidos en sprecialArray[], la relación entre el recuento de caracteres especiales y la longitud de la substring para cada substring siempre será 1. 
Por lo tanto, la suma de la relación = Número de substrings * 1 = 28.

Entrada: str = “abcd”, specialArray[] = {‘b’, ‘c’} 
Salida: 5.83333 
 

Enfoque: 
siga los pasos a continuación para resolver el problema:  

  • Para cada longitud posible de substrings de 1 a N, encuentre el recuento de caracteres especiales en cada substring de longitud x y agregue la proporción de conteo y x a la respuesta.
  • Para encontrar el recuento de caracteres especiales en cada substring en tiempo constante, cree una array de suma de prefijos del recuento de caracteres especiales usando la relación:

prefijo[i] = prefijo[i – 1] + especial(s[i]); 

  • Calcular el recuento de caracteres especiales en una substring dentro de los índices [i, j] viene dado por la relación:

prefijo[j – 1] – prefijo[i – 1] 
Por lo tanto, la relación entre el recuento de caracteres especiales y la longitud de la substring, 
f(i, j) = (prefijo[j – 1] – prefijo[i – 1] )/(j – yo + 1) 

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ Program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
const int N = 1e5 + 5;
 
// Stores frequency of special
// characters in the array
vector<int> prefix(N, 0);
 
// Stores prefix sum
vector<int> sum(N, 0);
 
// Function to check whether a character
// is special or not
bool isSpecial(char c,
               vector<char>& special)
{
    for (auto& i : special)
 
        // If current character
        // is special
        if (i == c)
            return true;
 
    // Otherwise
    return false;
}
 
// Function to find sum of ratio of
// count of special characters and
// length of substrings
double countRatio(string& s,
                  vector<char>& special)
{
 
    int n = s.length();
    for (int i = 0; i < n; i++) {
 
        // Calculate the prefix sum of
        // special nodes
        prefix[i] = int(isSpecial(s[i],
                                  special));
        if (i > 0)
            prefix[i] += prefix[i - 1];
    }
 
    for (int i = 0; i < n; i++) {
 
        // Generate prefix sum array
        sum[i] = prefix[i];
        if (i > 0)
            sum[i] += sum[i - 1];
    }
 
    double ans = 0;
    for (int i = 1; i <= n; i++) {
 
        // Calculate ratio for substring
        int count = sum[n - 1]
                    - (i > 1 ? sum[i - 2] : 0);
        count
            -= (i < n ? sum[n - i - 1] : 0);
 
        ans += double(count) / double(i);
    }
 
    return ans;
}
 
// Driver Code;
int main()
{
    string s = "abcd";
    vector<char> special = { 'b', 'c' };
 
    double ans = countRatio(s, special);
 
    cout << fixed << setprecision(6)
         << ans << endl;
 
    return 0;
}

Java

// Java Program to implement
// the above approach
import java.util.*;
class GFG{
 
static int N = 1000000 + 5;
 
// Stores frequency of special
// characters in the array
static int []prefix = new int[N];
   
// Stores prefix sum
static int []sum = new int[N];
 
// Function to check
// whether a character
// is special or not
static int isSpecial(char c,
                     char[] special)
{
  for (char i : special)
 
    // If current character
    // is special
    if (i == c)
      return 1;
 
  // Otherwise
  return 0;
}
 
// Function to find sum of ratio of
// count of special characters and
// length of subStrings
static  double countRatio(char []s,
                          char[] special)
{
  int n = s.length;
  for (int i = 0; i < n; i++)
  {
    // Calculate the prefix sum of
    // special nodes
    prefix[i] = (isSpecial(s[i],
                 special));
    if (i > 0)
      prefix[i] += prefix[i - 1];
  }
 
  for (int i = 0; i < n; i++)
  {
    // Generate prefix sum array
    sum[i] = prefix[i];
    if (i > 0)
      sum[i] += sum[i - 1];
  }
 
  double ans = 0;
  for (int i = 1; i <= n; i++)
  {
    // Calculate ratio for subString
    int count = sum[n - 1] - (i > 1 ?
                sum[i - 2] : 0);
    count -= (i < n ?
              sum[n - i - 1] : 0);
    ans += (double)count / (double)i;
  }
 
  return ans;
}
 
// Driver Code;
public static void main(String[] args)
{
  String s = "abcd";
  char[] special = {'b', 'c'};
  double ans = countRatio(s.toCharArray(),
                          special);
  System.out.format("%.6f",ans);
}
}
 
// This code is contributed by gauravrajput1

Python3

# Python3 program to implement
# the above approach
N = 100005
 
# Stores frequency of special
# characters in the array
prefix = [0] * N
 
# Stores prefix sum
sum = [0] * N
 
# Function to check whether a character
# is special or not
def isSpecial(c, special):
 
    for i in special:
 
        # If current character
        # is special
        if (i == c):
            return True
 
    # Otherwise
    return False
 
# Function to find sum of ratio of
# count of special characters and
# length of substrings
def countRatio(s, special):
 
    n = len(s)
    for i in range(n):
 
        # Calculate the prefix sum of
        # special nodes
        prefix[i] = int(isSpecial(s[i],
                                  special))
        if (i > 0):
            prefix[i] += prefix[i - 1]
 
    for i in range(n):
 
        # Generate prefix sum array
        sum[i] = prefix[i]
        if (i > 0):
            sum[i] += sum[i - 1]
 
    ans = 0
    for i in range(1, n + 1):
 
        # Calculate ratio for substring
        if i > 1:
            count = sum[n - 1]- sum[i - 2]
        else:
            count = sum[n - 1]
        if i < n:
            count -= sum[n - i - 1]
 
        ans += count / i
     
    return ans
 
# Driver Code
if __name__ == "__main__":
     
    s = "abcd"
    special = [ 'b', 'c' ]
 
    ans = countRatio(s, special)
 
    print('%.6f' % ans)
 
# This code is contributed by chitranayal

C#

// C# Program to implement
// the above approach
using System;
 
class GFG{
 
static int N = 1000000 + 5;
 
// Stores frequency of special
// characters in the array
static int []prefix = new int[N];
   
// Stores prefix sum
static int []sum = new int[N];
 
// Function to check
// whether a character
// is special or not
static int isSpecial(char c,
                     char[] special)
{
  foreach(char i in special)
     
    // If current character
    // is special
    if (i == c)
      return 1;
 
  // Otherwise
  return 0;
}
 
// Function to find sum of ratio of
// count of special characters and
// length of subStrings
static  double countRatio(char []s,
                          char[] special)
{
  int n = s.Length;
  for(int i = 0; i < n; i++)
  {
     
    // Calculate the prefix sum of
    // special nodes
    prefix[i] = (isSpecial(s[i],
                 special));
    if (i > 0)
      prefix[i] += prefix[i - 1];
  }
 
  for(int i = 0; i < n; i++)
  {
     
    // Generate prefix sum array
    sum[i] = prefix[i];
     
    if (i > 0)
      sum[i] += sum[i - 1];
  }
 
  double ans = 0;
  for(int i = 1; i <= n; i++)
  {
     
    // Calculate ratio for subString
    int count = sum[n - 1] - (i > 1 ?
                sum[i - 2] : 0);
    count -= (i < n ?
              sum[n - i - 1] : 0);
    ans += (double)count / (double)i;
  }
  return ans;
}
 
// Driver Code;
public static void Main(String[] args)
{
  String s = "abcd";
  char[] special = {'b', 'c'};
  double ans = countRatio(s.ToCharArray(),
                          special);
   
  Console.WriteLine("{0:F6}", ans);
}
}
 
// This code is contributed by Princi Singh

Javascript

<script>
  
// Javascript program to implement
// the above approach
var N = 1000005;
 
// Stores frequency of special
// characters in the array
var prefix = Array(N).fill(0);
 
// Stores prefix sum
var sum = Array(N).fill(0);
 
// Function to check whether a character
// is special or not
function isSpecial(c, special)
{  
    var ans = false;
    special.forEach(i => {
         
        // If current character
        // is special
        if (i == c)
            ans =true;
    });
 
    // Otherwise
    return ans;
 
}
 
// Function to find sum of ratio of
// count of special characters and
// length of substrings
function countRatio(s, special)
{
    var n = s.length;
    for(var i = 0; i < n; i++)
    {
         
        // Calculate the prefix sum of
        // special nodes
        prefix[i] = (isSpecial(s[i],
                               special));
        if (i > 0)
            prefix[i] += prefix[i - 1];
    }
 
    for(var i = 0; i < n; i++)
    {
         
        // Generate prefix sum array
        sum[i] = prefix[i];
         
        if (i > 0)
            sum[i] += sum[i - 1];
    }
 
    var ans = 0;
    for(var i = 1; i <= n; i++)
    {
         
        // Calculate ratio for substring
        var count = sum[n - 1] -
         ((i > 1) ? sum[i - 2] : 0);
         
        count -= ((i < n) ? sum[n - i - 1] : 0);
         
        ans += ((count) / (i));
    }
    return ans;
}
 
// Driver Code;
var s = "abcd";
var special = [ 'b', 'c' ];
var ans = countRatio(s.split(''), special);
 
document.write( ans.toFixed(6));
 
// This code is contributed by itsok
 
</script>
Producción: 

5.833333

 

Complejidad temporal: O(N) 
Complejidad espacial: O(N)
 

Publicación traducida automáticamente

Artículo escrito por insiderpants y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *