En este artículo vamos a ver cómo calcular informes de clasificación y arrays de confusión de tamaño 3*3 en Python.
Array de confusión e informe de clasificación, dos son funciones de biblioteca muy utilizadas e importantes disponibles en la biblioteca de aprendizaje de scikit. Pero, ¿cuántos de esos usuarios realmente pueden implementar estas dos funciones desde cero? Ahí está el problema. Solo el 40% de los entusiastas de ML podrán hacerlo. Muchos ni siquiera saben la teoría detrás de estos. En este artículo, implementaremos estas dos funciones desde cero y compararemos el resultado usando también funciones de biblioteca.
Planteamiento del problema
Dado el conjunto de datos del iris en formato .csv. Nuestro objetivo es clasificar las especies de flores y desarrollar una array de confusión y un informe de clasificación desde cero sin utilizar las funciones de la biblioteca de Python. Además, compare el resultado de las funciones temporales con las funciones estándar de la biblioteca.
El conjunto de datos Iris es el conjunto de datos multiclase. Hay 5 columnas en el conjunto de datos. Las primeras cuatro columnas representan las propiedades de las especies de flores: largo del pétalo, ancho del pétalo, largo del sépalo y ancho del sépalo. La última columna indica la etiqueta de clase de la flor. Hay 3 clases diferentes de especies de flores: Virginica, Setosa y Versicolor.
Ejemplos de array de confusión:
Entrada: y_verdadero = {2, 0, 2, 2, 0, 1}
y_pred = {0, 0, 2, 2, 0, 2}
Salida: confusion_matrix:
{
{2, 0, 0},
{0, 0, 1},
{1, 0, 2}
}
Explicación:
- La fila indica los valores reales de los datos y las columnas indican los datos pronosticados.
- Hay tres etiquetas, es decir, 0, 1 y 2.
- Los datos reales de la etiqueta 0 se predicen como: 2, 0, 0; Se pronostican 2 puntos como clase-0, 0 puntos como clase-1, 0 puntos como clase-2.
- La segunda fila {0, 0, 1} dice que: 0 puntos de clase-1 se predicen como clase-0 y clase-1. 1 punto de clase-1 se predice como clase-2.
- 3ra fila {1, 0, 2}:
- 1 punto de clase-2 se predice a clase-0.
- 0 punto de la clase 2 se predice para la clase 1.
- Se pronostican 2 puntos de clase-2 a clase-2.
Entrada: y_true = [“gato”, “hormiga”, “gato”, “gato”, “hormiga”, “pájaro”]
y_pred = [“hormiga”, “hormiga”, “gato”, “gato”, “hormiga”, “gato”]
Salida: confusion_matrix (y_true, y_pred, etiquetas=[“hormiga”, “pájaro”, “gato”])
{ hormiga pájaro gato
‘hormiga’= {2, 0, 0},
‘pájaro’= {0, 0, 1},
‘gato’= {1, 0, 2}}
Explicación:
- Hay 2 hormigas en el conjunto de datos real. Del total, 2 se pronostican como hormiga, 0 se pronostican como pájaro y gato.
- Hay 1 ave en el conjunto de datos real. Fuera de eso, 0 se predicen como hormiga y pájaro. 1 se predice como cat.
- Hay 3 gatos en el conjunto de datos real. De eso, 1 se predice como hormiga, 2 se predice como gato.
¿Qué es un informe de clasificación?
Como sugiere el nombre, es el informe el que explica todo sobre la clasificación. Este es el resumen de la calidad de la clasificación realizada por el modelo ML construido. Se compone principalmente de 5 columnas y (N+3) filas. La primera columna es el nombre de la etiqueta de la clase, seguida de Precisión, Recuperación, Puntuación F1 y Soporte. N filas son para N etiquetas de clase y otras tres filas son para precisión, promedio macro y promedio ponderado.
Precisión: Se calcula con respecto a los valores predichos. Para la clase A, de las predicciones totales, cuántas realmente pertenecen a la clase A en el conjunto de datos real, se define como la precisión. Es la relación entre la celda [i][i] de la array de confusión y la suma de la columna [i].
Recuperación: se calcula con respecto a los valores reales en el conjunto de datos. Para la clase A, del total de entradas en el conjunto de datos, cuántas fueron realmente clasificadas en la clase A por el modelo ML, se define como recuperación. Es la relación entre la celda [i][i] de la array de confusión y la suma de la fila [i].
F1-score: Es la media armónica de precisión y recuperación.
Soporte: Son las entradas totales de cada clase en el conjunto de datos real. Es simplemente la suma de filas para cada clase-i.
Ejemplos de informes de clasificación:
Entrada: confusión [][]= {
{1, 0, 0},
{1, 0, 0},
{0, 1, 2}
};
Salida :
recuperación de precisión compatibilidad con puntuación f1
clase 0 0,50 1,00 0,67 1
clase 1 0,00 0,00 0,00 1
clase 2 1,00 0,67 0,80 3
precisión 0,60 5
promedio macro 0.50 0.56 0.49 5
promedio ponderado 0,70 0,60 0,61 5
Confusión de entrada [][]= {
{0, 1},
{0, 2}
};
Producción:
recuperación de precisión compatibilidad con puntuación f1
1 1,00 0,67 0,80 3
2 0,00 0,00 0,00 0
3 0,00 0,00 0,00 0
precisión 0,67
promedio macro 0.33 0.22 0.27 3
promedio ponderado 1,00 0,67 0,80 3
A continuación se muestra la implementación del código.
Python3
# Our aim is to build the function
# for calculating the confusion_matrix
# and classification_report
# for multiclass classification, like IRIS dataset.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import classification_report
# Function for confusion matrix
def Confusion_matrix(y_test, y_pred, target_names=None):
# target_names is a list.
# actual values are arranged in the rows.
# predicted values are arranged in the columns.
# if there are m classes, then cm is m*m matrix.
if target_names == None:
m = len(set(y_test))
else:
m = len(target_names)
size = len(y_test)
matrix = dict()
# create matrix initialised with 0
for class_name in range(m):
matrix[class_name] = [0 for k in range(m)]
# populating the matrix.
for i in range(size):
actual_class = y_test[i]
pred_class = y_pred[i]
matrix[actual_class][pred_class] += 1
# Change the name of columns.
if target_names == None:
# Now, lets print the confusion matrix.
print("Confusion Matrix of given model is :")
if m == 3:
print("Count=%-14d %-15s %-15s %-15s" % (size,
'0', '1',
'2'))
for key, value in matrix.items():
print("Actual %-13s %-15d %-15d %-15d" %
(key, value[0], value[1], value[2]))
elif m == 2:
print("Count=%-14d %-15s %-15s" % (size, '0', '1'))
for key, value in matrix.items():
print("Actual %-13s %-15d %-15d" % (key, value[0],
value[1]))
else:
matrix = dict(zip(target_names, list(matrix.values())))
# Now, lets print the confusion matrix.
print("Confusion Matrix of given model is :")
print("Count=%-14d %-15s %-15s %-15s" %
(size, target_names[0], target_names[1], target_names[2]))
for key, value in matrix.items():
print("Actual %-13s %-15d %-15d %-15d" %
(key, value[0], value[1], value[2]))
return matrix
# Function for performance report.
def performance_report(cm):
col = len(cm)
# col=number of class
arr = []
for key, value in cm.items():
arr.append(value)
cr = dict()
support_sum = 0
# macro avg of support is
# sum of support only, not the mean.
macro = [0]*3
# weighted avg of support is
# sum of support only, not the mean.
weighted = [0]*3
for i in range(col):
vertical_sum= sum([arr[j][i] for j in range(col)])
horizontal_sum= sum(arr[i])
p = arr[i][i] / vertical_sum
r = arr[i][i] / horizontal_sum
f = (2 * p * r) / (p + r)
s = horizontal_sum
row=[p,r,f,s]
support_sum+=s
for j in range(3):
macro[j]+=row[j]
weighted[j]+=row[j]*s
cr[i]=row
# add Accuracy parameters.
truepos=0
total=0
for i in range(col):
truepos+=arr[i][i]
total+=sum(arr[i])
cr['Accuracy']=["", "", truepos/total, support_sum]
# Add macro-weight and weighted_avg features.
macro_avg=[Sum/col for Sum in macro]
macro_avg.append(support_sum)
cr['Macro_avg']=macro_avg
weighted_avg=[Sum/support_sum for Sum in weighted]
weighted_avg.append(support_sum)
cr['Weighted_avg']=weighted_avg
# print the classification_report
print("Performance report of the model is :")
space,p,r,f,s=" ","Precision","Recall","F1-Score","Support"
print("%13s %9s %9s %9s %9s\n"%(space,p,r,f,s))
stop=0
for key,value in cr.items():
if stop<col:
stop+=1
print("%13s %9.2f %9.2f %9.2f %9d"%(key,value[0],
value[1],
value[2],
value[3]))
elif stop==col:
stop+=1
print("\n%13s %9s %9s %9.2f %9d"%(key,value[0],
value[1],
value[2],
value[3]))
else:
print("%13s %9.2f %9.2f %9.2f %9d"%(key,
value[0],
value[1],
value[2],
value[3]))
# from sklearn.metrics import
# confusion_matrix,classification_report
# Main Function is here.
def main():
dataset=load_iris()
X,y,classes=dataset['data'],dataset['target'],
dataset['target_names']
X_train,X_test,y_train,y_test=train_test_split(
X,y,shuffle=True,random_state=5,test_size=0.3)
model=GaussianNB().fit(X_train,y_train)
y_pred=model.predict(X_test)
classes=list(classes)
cm=Confusion_matrix(y_test, y_pred, classes)
cr=performance_report(cm)
print("\nCR by library method=\n",
classification_report(y_test, y_pred))
if __name__ == '__main__':
main()
Producción:
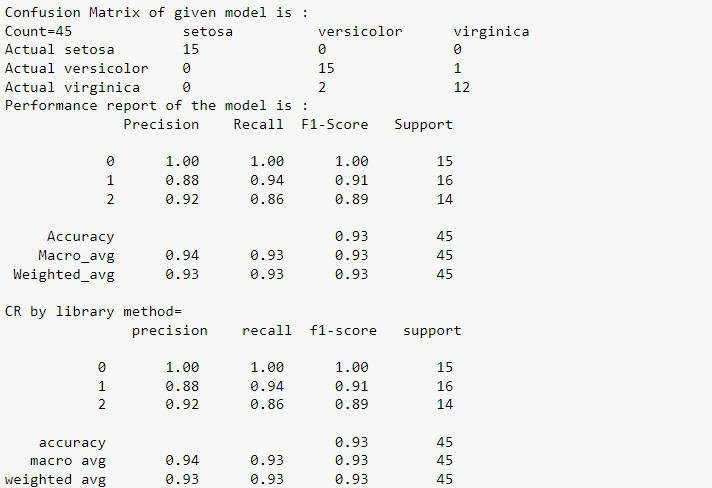
Complejidad del tiempo: O(N*N)
Complejidad espacial: (N*4), para cada etiqueta necesitamos una array de tamaño 4.
Publicación traducida automáticamente
Artículo escrito por pintusaini y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA