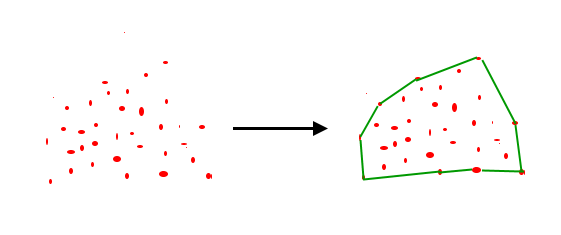
Dado un conjunto de puntos en el plano. la envolvente convexa del conjunto es el polígono convexo más pequeño que contiene todos los puntos del mismo.
Recomendamos encarecidamente ver la siguiente publicación primero.
¿Cómo verificar si dos segmentos de línea dados se cruzan?
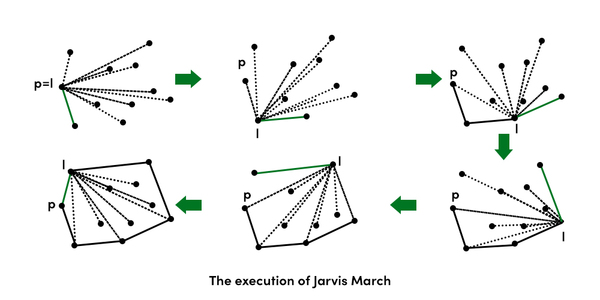
La idea del Algoritmo de Jarvis es simple, comenzamos desde el punto más a la izquierda (o el punto con el valor mínimo de la coordenada x) y seguimos envolviendo los puntos en dirección contraria a las manecillas del reloj.
La gran pregunta es, dado un punto p como punto actual, ¿cómo encontrar el siguiente punto en la salida?
La idea es usar la orientación() aquí. El siguiente punto se selecciona como el punto que supera a todos los demás puntos en sentido antihorario, es decir, el siguiente punto es q si para cualquier otro punto r, tenemos «orientación (p, q, r) = antihorario».
Algoritmo:
Paso 1) Inicialice p como el punto más a la izquierda.
Paso 2) Siga mientras no volvamos al primer punto (o más a la izquierda).
2.1) El siguiente punto q es el punto, tal que el triplete (p, q, r) es en sentido antihorario para cualquier otro punto r.
Para encontrar esto, simplemente inicializamos q como el siguiente punto, luego recorremos todos los puntos.
Para cualquier punto i, si i es más en sentido contrario a las agujas del reloj, es decir, la orientación (p, i, q) es en sentido contrario a las agujas del reloj, entonces actualizamos q como i.
Nuestro valor final de q va a ser el punto más contrario a las agujas del reloj.
2.2) next[p] = q (Almacenar q como siguiente de p en el casco convexo de salida).
2.3) p = q (Establezca p como q para la próxima iteración).
A continuación se muestra la implementación del algoritmo anterior.
C++
// A C++ program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
#include <bits/stdc++.h>
using namespace std;
struct Point
{
int x, y;
};
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // collinear
return (val > 0)? 1: 2; // clock or counterclock wise
}
// Prints convex hull of a set of n points.
void convexHull(Point points[], int n)
{
// There must be at least 3 points
if (n < 3) return;
// Initialize Result
vector<Point> hull;
// Find the leftmost point
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
// Start from leftmost point, keep moving counterclockwise
// until reach the start point again. This loop runs O(h)
// times where h is number of points in result or output.
int p = l, q;
do
{
// Add current point to result
hull.push_back(points[p]);
// Search for a point 'q' such that orientation(p, q,
// x) is counterclockwise for all points 'x'. The idea
// is to keep track of last visited most counterclock-
// wise point in q. If any point 'i' is more counterclock-
// wise than q, then update q.
q = (p+1)%n;
for (int i = 0; i < n; i++)
{
// If i is more counterclockwise than current q, then
// update q
if (orientation(points[p], points[i], points[q]) == 2)
q = i;
}
// Now q is the most counterclockwise with respect to p
// Set p as q for next iteration, so that q is added to
// result 'hull'
p = q;
} while (p != l); // While we don't come to first point
// Print Result
for (int i = 0; i < hull.size(); i++)
cout << "(" << hull[i].x << ", "
<< hull[i].y << ")\n";
}
// Driver program to test above functions
int main()
{
Point points[] = {{0, 3}, {2, 2}, {1, 1}, {2, 1},
{3, 0}, {0, 0}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
convexHull(points, n);
return 0;
}
Java
// Java program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
import java.util.*;
class Point
{
int x, y;
Point(int x, int y){
this.x=x;
this.y=y;
}
}
class GFG {
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
public static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // collinear
return (val > 0)? 1: 2; // clock or counterclock wise
}
// Prints convex hull of a set of n points.
public static void convexHull(Point points[], int n)
{
// There must be at least 3 points
if (n < 3) return;
// Initialize Result
Vector<Point> hull = new Vector<Point>();
// Find the leftmost point
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
// Start from leftmost point, keep moving
// counterclockwise until reach the start point
// again. This loop runs O(h) times where h is
// number of points in result or output.
int p = l, q;
do
{
// Add current point to result
hull.add(points[p]);
// Search for a point 'q' such that
// orientation(p, q, x) is counterclockwise
// for all points 'x'. The idea is to keep
// track of last visited most counterclock-
// wise point in q. If any point 'i' is more
// counterclock-wise than q, then update q.
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
// If i is more counterclockwise than
// current q, then update q
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
// Now q is the most counterclockwise with
// respect to p. Set p as q for next iteration,
// so that q is added to result 'hull'
p = q;
} while (p != l); // While we don't come to first
// point
// Print Result
for (Point temp : hull)
System.out.println("(" + temp.x + ", " +
temp.y + ")");
}
/* Driver program to test above function */
public static void main(String[] args)
{
Point points[] = new Point[7];
points[0]=new Point(0, 3);
points[1]=new Point(2, 3);
points[2]=new Point(1, 1);
points[3]=new Point(2, 1);
points[4]=new Point(3, 0);
points[5]=new Point(0, 0);
points[6]=new Point(3, 3);
int n = points.length;
convexHull(points, n);
}
}
// This code is contributed by Arnav Kr. Mandal.
Python3
# Python3 program to find convex hull of a set of points. Refer # https://www.geeksforgeeks.org/orientation-3-ordered-points/ # for explanation of orientation() # point class with x, y as point class Point: def __init__(self, x, y): self.x = x self.y = y def Left_index(points): ''' Finding the left most point ''' minn = 0 for i in range(1,len(points)): if points[i].x < points[minn].x: minn = i elif points[i].x == points[minn].x: if points[i].y > points[minn].y: minn = i return minn def orientation(p, q, r): ''' To find orientation of ordered triplet (p, q, r). The function returns following values 0 --> p, q and r are collinear 1 --> Clockwise 2 --> Counterclockwise ''' val = (q.y - p.y) * (r.x - q.x) - \ (q.x - p.x) * (r.y - q.y) if val == 0: return 0 elif val > 0: return 1 else: return 2 def convexHull(points, n): # There must be at least 3 points if n < 3: return # Find the leftmost point l = Left_index(points) hull = [] ''' Start from leftmost point, keep moving counterclockwise until reach the start point again. This loop runs O(h) times where h is number of points in result or output. ''' p = l q = 0 while(True): # Add current point to result hull.append(p) ''' Search for a point 'q' such that orientation(p, q, x) is counterclockwise for all points 'x'. The idea is to keep track of last visited most counterclock- wise point in q. If any point 'i' is more counterclock- wise than q, then update q. ''' q = (p + 1) % n for i in range(n): # If i is more counterclockwise # than current q, then update q if(orientation(points[p], points[i], points[q]) == 2): q = i ''' Now q is the most counterclockwise with respect to p Set p as q for next iteration, so that q is added to result 'hull' ''' p = q # While we don't come to first point if(p == l): break # Print Result for each in hull: print(points[each].x, points[each].y) # Driver Code points = [] points.append(Point(0, 3)) points.append(Point(2, 2)) points.append(Point(1, 1)) points.append(Point(2, 1)) points.append(Point(3, 0)) points.append(Point(0, 0)) points.append(Point(3, 3)) convexHull(points, len(points)) # This code is contributed by # Akarsh Somani, IIIT Kalyani
C#
// C# program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
using System;
using System.Collections.Generic;
public class Point
{
public int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class GFG
{
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
public static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // collinear
return (val > 0)? 1: 2; // clock or counterclock wise
}
// Prints convex hull of a set of n points.
public static void convexHull(Point []points, int n)
{
// There must be at least 3 points
if (n < 3) return;
// Initialize Result
List<Point> hull = new List<Point>();
// Find the leftmost point
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
// Start from leftmost point, keep moving
// counterclockwise until reach the start point
// again. This loop runs O(h) times where h is
// number of points in result or output.
int p = l, q;
do
{
// Add current point to result
hull.Add(points[p]);
// Search for a point 'q' such that
// orientation(p, q, x) is counterclockwise
// for all points 'x'. The idea is to keep
// track of last visited most counterclock-
// wise point in q. If any point 'i' is more
// counterclock-wise than q, then update q.
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
// If i is more counterclockwise than
// current q, then update q
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
// Now q is the most counterclockwise with
// respect to p. Set p as q for next iteration,
// so that q is added to result 'hull'
p = q;
} while (p != l); // While we don't come to first
// point
// Print Result
foreach (Point temp in hull)
Console.WriteLine("(" + temp.x + ", " +
temp.y + ")");
}
/* Driver code */
public static void Main(String[] args)
{
Point []points = new Point[7];
points[0]=new Point(0, 3);
points[1]=new Point(2, 3);
points[2]=new Point(1, 1);
points[3]=new Point(2, 1);
points[4]=new Point(3, 0);
points[5]=new Point(0, 0);
points[6]=new Point(3, 3);
int n = points.Length;
convexHull(points, n);
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// Javascript program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
class Point
{
constructor(x, y)
{
this.x = x;
this.y = y;
}
}
// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
function orientation(p, q, r)
{
let val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0; // collinear
return (val > 0)? 1: 2; // clock or counterclock wise
}
// Prints convex hull of a set of n points.
function convexHull(points, n)
{
// There must be at least 3 points
if (n < 3) return;
// Initialize Result
let hull = [];
// Find the leftmost point
let l = 0;
for (let i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
// Start from leftmost point, keep moving
// counterclockwise until reach the start point
// again. This loop runs O(h) times where h is
// number of points in result or output.
let p = l, q;
do
{
// Add current point to result
hull.push(points[p]);
// Search for a point 'q' such that
// orientation(p, q, x) is counterclockwise
// for all points 'x'. The idea is to keep
// track of last visited most counterclock-
// wise point in q. If any point 'i' is more
// counterclock-wise than q, then update q.
q = (p + 1) % n;
for (let i = 0; i < n; i++)
{
// If i is more counterclockwise than
// current q, then update q
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
// Now q is the most counterclockwise with
// respect to p. Set p as q for next iteration,
// so that q is added to result 'hull'
p = q;
} while (p != l); // While we don't come to first
// point
// Print Result
for (let temp of hull.values())
document.write("(" + temp.x + ", " +
temp.y + ")<br>");
}
/* Driver program to test above function */
let points = new Array(7);
points[0] = new Point(0, 3);
points[1] = new Point(2, 3);
points[2] = new Point(1, 1);
points[3] = new Point(2, 1);
points[4] = new Point(3, 0);
points[5] = new Point(0, 0);
points[6] = new Point(3, 3);
let n = points.length;
convexHull(points, n);
// This code is contributed by avanitrachhadiya2155
</script>
Salida: La salida son puntos del casco convexo.
(0, 3) (0, 0) (3, 0) (3, 3)
Complejidad de tiempo: O(m * n) , donde n es el número de puntos de entrada y m es el número de puntos de salida o casco (m <= n). Para cada punto del casco, examinamos todos los demás puntos para determinar el siguiente punto.
Peor caso, Complejidad temporal: O(n 2 ) . El peor caso ocurre cuando todos los puntos están en el casco (m = n).
Espacio auxiliar: O(n)
Set 2- Casco convexo (Graham Scan)
Nota : El código anterior puede producir resultados diferentes para diferentes órdenes de entradas, cuando hay puntos colineales en el casco convexo. Por ejemplo, produce una salida como (0, 3) (0, 0) (3, 0) (3, 3) para la entrada (0, 3), (0, 0), (0, 1), (3, 0), (3, 3) y salida como (0, 3) (0, 1) (0, 0) (3, 0) (3, 3) para entrada como (0, 3), (0, 1) , (0, 0), (3, 0), (3, 3). Generalmente necesitamos el siguiente punto más lejano en el caso de colineales, podemos obtener el resultado deseado en el caso de puntos colineales agregando una condición if más. Consulte este código modificado.
Fuentes:
http://www.cs.uiuc.edu/~jeffe/teaching/373/notes/x05-convexhull.pdf
http://www.dcs.gla.ac.uk/~pat/52233/slides/Hull1x1 .pdf
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA