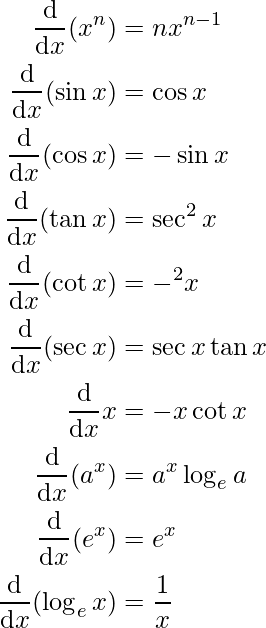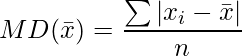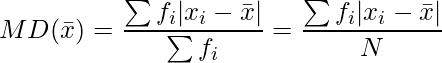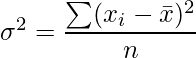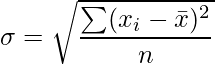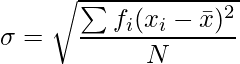GeeksforGeeks trae una hoja de Fórmula para estudiantes de Matemáticas de Clase 11 , que se basa estrictamente en el plan de estudios NCERT para facilitar el proceso de preparación y revisión de los estudiantes para los exámenes escolares, así como varios exámenes competitivos como JEE y NEET. Este artículo no solo incluye la lista de fórmulas, sino que ofrece a los estudiantes un resumen de los capítulos, puntos importantes para recordar, una breve explicación de conceptos importantes y derivaciones de fórmulas para una mejor comprensión y retención de los capítulos. Por lo tanto, estas fórmulas matemáticas CBSE Clase 11 por capítulos están preparadas para garantizar la máxima preparación y buenas calificaciones en cualquier examen.

Capítulo 1: Conjuntos
El capítulo explica el concepto de conjuntos junto con su representación . Los temas tratados son conjuntos vacíos, conjuntos iguales, subconjuntos, conjuntos finitos e infinitos, conjuntos potencia y conjuntos universales . Un conjunto es una colección bien coordinada de objetos. Un conjunto formado por elementos definidos es un conjunto finito. De lo contrario, es un conjunto infinito. A continuación se enumeran los términos y propiedades importantes que se utilizan en los conjuntos:
- Se dice que la unión de dos conjuntos A y B contiene elementos que están en el conjunto A y en el conjunto B. La unión de A y B se denota como A∪B.
- Se dice que la intersección de dos conjuntos A y B contiene elementos que son comunes en ambos conjuntos. La intersección de A y B se denota como A∩B.
- El complemento de un conjunto A es el conjunto de todos los elementos dados en el conjunto universal U que no están contenidos en A. El complemento de A se denota como A’.
- Para cualesquiera dos conjuntos A y B, se cumple lo siguiente:
- (A∪B)′=A′∩B′
- (A∩B)′=A′∪B′
- Si se dan los conjuntos finitos A y B tales que, (A∩B)=ϕ , entonces:
n(A∪B)=n(A)+n(B)
- Si (A∪B)=ϕ , entonces:
n(A∪B)=n(A)+n(B)−n(A∩B)
- Algunas otras fórmulas importantes de Conjuntos para cualquiera de los tres conjuntos A, B y C son las siguientes:
- A – A = Ø
- segundo – un = segundo⋂ un’
- B – A = B – (A⋂B)
- (A – B) = A si A⋂B = Ø
- (A – B) ⋂ C = (A⋂ C) – (B⋂ C)
- A ΔB = (AB) U (B-A)
- n(A∪B) = n(A) + n(B) – n(A⋂B)
- n(A∪B∪C)= n(A) +n(B) + n(C) – n(B⋂C) – n (A⋂B)- n (A⋂C) + n(A⋂B ⋂C)
- n(A – B) = n(A∪B) – n(B)
- n(A – B) = n(A) – n(A⋂B)
- n(A’) = n(∪) – n(A)
- n(U) = n(A) + n(B) + – n(A⋂B) + n((A∪B)’)
- n((A∪B)’) = n(U) + n(A⋂B) – n(A) – n(B)
Capítulo 2: Relaciones y Funciones
El capítulo Relaciones y funciones explica los conceptos avanzados de la teoría de conjuntos utilizando el concepto de pares de elementos ordenados y no ordenados. Un par ordenado es un par de elementos agrupados en un cierto orden. Una relación R hacia un conjunto A con un conjunto B puede describirse como un subconjunto del producto cartesiano A × B que se obtiene describiendo una relación entre el primero de su elemento x y el segundo de su elemento y dado en los pares ordenados de A × B.
Las propiedades mencionadas a continuación seguramente ayudarán a los estudiantes a resolver varios problemas matemáticos:
- Relaciones: Una relación R es el subconjunto del producto cartesiano de A × B, donde A y B son dos elementos no vacíos. Se obtiene estableciendo la relación entre el primer elemento y el segundo elemento del par ordenado de A × B.
- Inverso de la relación: A y B son dos conjuntos no vacíos cualesquiera. Sea R una relación entre dos conjuntos A y B. La inversa de la relación R, indicada como R -1 , es una relación que conecta B y A y está definida por
R – 1 ={(b, a) : (a, b) ∈ R}
donde, Dominio de R = Rango de R -1 y Rango de R = Dominio de R -1 .
- Funciones: Se dice que una relación f de un conjunto A con un conjunto B es función, si cada elemento del conjunto A tiene una y única imagen en el conjunto B.
- Un producto cartesiano A × B de dos conjuntos A y B está dado por: A × B = { (a,b) : a ϵ A, b ϵ B}
- Si (a, b) = (x, y); entonces a = x y b = y
- Si n(A) = x y n(B) = y, entonces n(A × B) = xy y A × ϕϕ = ϕϕ
- El producto cartesiano: A × B ≠ B × A.
- Una función f del conjunto A al conjunto B considera un tipo de relación específico donde cada elemento x en el conjunto A tiene una y solo una imagen en el conjunto B. Una función se puede denotar como f : A → B, donde f(x) = y .
- Álgebra de funciones: Si la función f : X → R yg : X → R; tenemos:
- (f + g)(x) = f(x) + g(x) ; x ϵ X
- (f – g)(x) = f(x) – g(x)
- (f . g)(x) = f(x).g(x)
- (kf)(x) = k(f(x)) donde k es un número real
- {f/g}(x) = f(x)/g(x), g(x)≠0
Capítulo 3: Funciones trigonométricas
En Matemáticas, las funciones trigonométricas son las funciones reales que se relacionan con un ángulo de un triángulo rectángulo formando unas razones finitas de dos longitudes de los lados. Encuentre las fórmulas matemáticas importantes para la clase 11 relacionadas con las funciones trigonométricas a continuación.
- Si en un círculo de radio r, un arco de longitud l subtiende un ángulo de θ radianes, entonces l = r×θ .
- Medida en radianes = π/180 × Medida en grados
- Medida en grados = 180/π × Medida en radianes
- Razones trigonométricas:
- sen θ = (Perpendicular (P)) / (Hipotenusa (H)).
- cos θ = (Base (B)) / (Hipotenusa (H)).
- tan θ = (Perpendicular (P)) / (Base (B)).
- cosec θ = (Hipotenusa (H)) / (Perpendicular (P)).
- sec θ = (Hipotenusa (H)) / (Base (B)).
- cuna θ = (Base (B)) / (Perpendicular (P)).
- Razones trigonométricas recíprocas :
- sin θ = 1 / (coseg θ)
- cosec θ = 1 / (sen θ)
- cos θ = 1 / (seg θ)
- segundo θ = 1 / (cos θ)
- tan θ = 1 / (cuna θ)
- cuna θ = 1 / (bronceado θ)
- Razones trigonométricas de ángulos complementarios:
- sen (90 ° – θ) = cos θ
- cos (90 ° – θ) = sen θ
- bronceado (90 ° – θ) = cuna θ
- cuna (90 ° – θ) = tan θ
- segundo (90 ° – θ) = cosegundo θ
- cosec (90 ° – θ) = sec θ
- Razones trigonométricas periódicas
- sin(π/2-θ) = cos θ
- cos(π/2-θ) = sen θ
- sen(π-θ) = sen θ
- cos(π-θ) = -cos θ
- sen(π+θ)=-sen θ
- cos(π+θ)=-cos θ
- sin(2π-θ) = -sin θ
- cos(2π-θ) = cos θ
- Identidades trigonométricas
- sen 2 θ + cos 2 θ = 1 ⇒ sen 2 θ = 1 – cos 2 θ ⇒ cos 2 θ = 1 – sen 2 θ
- cosec 2 θ – cot 2 θ = 1 ⇒ cosec 2 θ = 1 + cot 2 θ ⇒ cot 2 θ = cosec 2 θ – 1
- segundo 2 θ – bronceado 2 θ = 1 ⇒ segundo 2 θ = 1 + bronceado 2 θ ⇒ bronceado 2 θ = segundo 2 θ – 1
- Fórmulas de producto a suma
- sen x sen y = 1/2 [cos(x–y) − cos(x+y)]
- cos x cos y = 1/2[cos(x–y) + cos(x+y)]
- sen x cos y = 1/2[sen(x+y) + sen(x−y)]
- cos x sen y = 1/2[sen(x+y) – sen(x−y)]
- Fórmulas de suma a producto
- sen x + sen y = 2 sen [(x+y)/2] cos [(xy)/2]
- sen x – sen y = 2 cos [(x+y)/2] sen [(xy)/2]
- cos x + cos y = 2 cos [(x+y)/2] cos [(xy)/2]
- cos x – cos y = -2 sen [(x+y)/2] sen [(xy)/2]
- Fórmulas trigonométricas generales:
- sen (x+y) = sen x × cos y + cos x × sen y
- cos(x+y)=cosx×cosy−senx×seny
- cos(x–y)=cosx×cosy+senx×seny
sin(x–y)=senx×cosy−cosx×seny- Si no hay ángulos x, y y (x ± y) es un múltiplo impar de (π / 2); después:
- tan (x+y) = tan x + tan y / 1 − tan x tan y
- tan (x−y) = tan x − tan y / 1 + tan x tan y
- Si no hay ángulos x, y y (x ± y) es un múltiplo impar de π; después:
- cuna (x+y) = cuna x cuna y−1 / cuna y + cuna x
- cuna (x−y) = cuna x cuna y+1 / cuna y − cuna x
- Fórmulas para el doble de los ángulos:
- sin2θ = 2sinθ cosθ = [2tan θ /(1+tan2θ)]
- cos2θ = cos2θ–sen2θ = 1–2sen2θ = 2cos2θ–1= [(1-tan2θ)/(1+tan2θ)]
- tan 2θ = (2 tan θ)/(1-tan 2θ)
- Fórmulas para el triple de los ángulos:
- sen 3θ = 3 sen θ – 4 sen 3θ
- cos 3θ = 4cos 3θ – 3cos θ
- tan 3θ = [3tan θ–tan 3θ]/[1−3tan 2θ]
Capítulo 4: Principio de Inducción Matemática
Como sugiere el nombre, el capítulo explica el concepto del Principio de Inducción Matemática . Los temas tratados son el proceso para probar la inducción y motivar la aplicación tomando los números naturales como el subconjunto menos inductivo de los números reales. Una base clave para el pensamiento matemático es el razonamiento deductivo. A diferencia de la deducción, el razonamiento inductivo depende de trabajar con diferentes casos y desarrollar una conjetura observando incidencias hasta que hayamos observado todos y cada uno de los casos. Así, en lenguaje sencillo podemos decir que la palabra ‘inducción’ significa la generalización a partir de casos o hechos particulares.
A continuación se menciona la lista de algunos términos y pasos importantes utilizados en el capítulo mencionado anteriormente:
- Declaración: Una oración se llama declaración si es verdadera o falsa.
- Motivación: La motivación es tender a iniciar una acción. Aquí el paso base nos motiva para la inducción matemática.
- Principio de inducción matemática: el principio de inducción matemática es una de esas herramientas que se puede utilizar para probar una amplia variedad de afirmaciones matemáticas. Cada uno de estos enunciados se asume como P(n) asociado con un entero positivo n, para el cual se examina la corrección para el caso n = 1. Entonces, asumiendo la verdad de P(k) para algún entero positivo k, se establece la verdad de P(k+1).
- Regla de trabajo:
- Paso 1: Demostrar que el enunciado dado es verdadero para n = 1.
- Paso 2: Suponga que el enunciado es verdadero para n = k.
- Paso 3: usando la suposición hecha en el paso 2, demuestre que el enunciado es verdadero para n = k + 1. Hemos probado que el enunciado es verdadero para n = k. Según el paso 3, también es cierto para k + 1 (es decir, 1 + 1 = 2). Repitiendo la lógica anterior, es cierto para todos los números naturales.
Capítulo 5: Números complejos y ecuaciones cuadráticas
Como sugiere el nombre del capítulo, por lo tanto, este capítulo explica el concepto de números complejos y ecuaciones cuadráticas y sus propiedades . Los temas tratados son la raíz cuadrada, las propiedades algebraicas, el plano argand y la representación polar de números complejos , soluciones de ecuaciones cuadráticas en el sistema de números complejos. Algunos puntos importantes relacionados con los números complejos y las ecuaciones cuadráticas son los siguientes:
- Números complejos : un número que se puede expresar en la forma a + b se conoce como número complejo; donde a y b son los números reales e i es la parte imaginaria del número complejo.
- Números imaginarios : la raíz cuadrada de un número real negativo se denomina número imaginario, por ejemplo, √-2, √-5, etc. La cantidad √-1 es una unidad imaginaria y se denota con ‘i’ llamada iota.
yo = √-1, yo 2 = -1, yo 3 = -i, yo 4 = 1
- Igualdad de Número Complejo: Dos números complejos z 1 = x 1 + iy 1 y z 2 = x 2 + iy 2 son iguales, si y si x 1 = x 2 y y 1 = y 2 es decir Re(z 1 ) = Re(z 2 ) e Im(z 1 ) = Im(z 2 )
- Suma: Considere que z 1 = x 1 + iy 1 y z 2 = x 2 + iy 2 son dos números complejos, entonces su suma se define como
z 1 + z 2 = (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + yo (y 1 + y 2 )
- Resta: Considere que z 1 = (x 1 + iy 1 ) y z 2 = (x 2 + iy 2 ) son dos números complejos, entonces su diferencia se define como
z 1 – z 2 = (x 1 + iy 1 ) – (x 2 + iy 2 ) = (x 1 – x 2 ) + i(y 1 – y 2 )
- Multiplicación: Considere z 1 = (x 1 + iy 1 ) y z 2 = (x 2 + iy 2 ) como dos números complejos cualesquiera, entonces su multiplicación se define como
z 1 z 2 = (x 1 + iy 1 ) (x 2 + iy 2 ) = (x 1 x 2 – y 1 y 2 ) + yo (x 1 y 2 + x 2 y 1 )
- División: Considere z 1 = x 1 + iy 1 y z 2 = x 2 + iy 2 como dos números complejos, entonces su división se define como
Considere z = x + iy, si ‘i’ se reemplaza por (-i), entonces se llama conjugado del número complejo z y se denota por z¯, es decir
Módulo de un número complejo
Considere z = x + y ser un número complejo. Entonces, la raíz cuadrada positiva de la suma del cuadrado de la parte real y el cuadrado de la parte imaginaria se llama módulo (valores absolutos) de z y se denota por |z| es decir
|z| = √x 2 + y 2
Cualquier número complejo z = x + y se puede representar geométricamente mediante un punto (x, y) en un plano, llamado plano de Argand o plano de Gauss.
- Un número x puro, es decir (x + 0i) está representado por el punto (x, 0) en el eje X. Por lo tanto, el eje X se llama eje real.
- Un número puramente imaginario y, es decir (0 + y) está representado por el punto (0, y) en el eje y. Por lo tanto, el eje y se llama eje imaginario.
Argumento de un número complejo
El ángulo formado por la línea que une el punto z con el origen, con la dirección positiva del eje X en sentido antihorario, se llama argumento o amplitud del número complejo. Se denota con el símbolo arg(z) o amp(z).
arg(z) = θ = tan -1 (y/x)
- Valor principal del argumento
- Cuando x > 0 y y > 0 ⇒ arg(z) = θ
- Cuando x < 0 y y > 0 ⇒ arg(z) = π – θ
- Cuando x < 0 y y < 0 ⇒ arg(z) = -(π – θ)
- Cuando x > 0 y y < 0 ⇒ arg(z) = -θ
Forma polar de un número complejo
Cuando z = x + iy es un número complejo, entonces z se puede escribir como,
- z = |z| (cosθ + isinθ) , donde θ = arg(z).
que se conoce como la forma polar. Ahora, cuando el valor general del argumento es θ, entonces la forma polar de z se escribe como,
- z = |z| [cos (2nπ + θ) + isin(2nπ + θ)] , donde n es un número entero.
Capítulo 6: Desigualdades lineales
El capítulo explica el concepto de Desigualdades Lineales . Los temas tratados son soluciones algebraicas y representación gráfica de Desigualdades Lineales en una variable y dos variables respectivamente. En matemáticas, una desigualdad es una relación que se mantiene entre dos valores cuando son diferentes. Resolver desigualdades lineales es muy similar a resolver ecuaciones lineales, excepto por un pequeño pero importante detalle: cambias el signo de desigualdad cada vez que multiplicas o divides la desigualdad por un negativo.
Inecuación: Una inecuación o desigualdad es una declaración que involucra variables y el signo de desigualdad como >, <, ≥ o ≤.
- Símbolos utilizados en las desigualdades
- El símbolo < significa menor que.
- El símbolo > significa mayor que.
- El símbolo < con una barra debajo ≤ significa menor o igual que.
- El símbolo > con una barra debajo ≥ significa mayor o igual que.
- El símbolo ≠ significa que las cantidades en los lados izquierdo y derecho no son iguales.
Soluciones algebraicas para desigualdades lineales en una variable y su representación gráfica
Usando el método de prueba y error, se puede determinar la solución a la desigualdad lineal. Sin embargo, este método no siempre es posible y calcular la solución lleva más tiempo. Entonces, usando un enfoque numérico, la desigualdad lineal se puede resolver. Al resolver desigualdades lineales, recuerda seguir estas reglas:
Regla 1: No cambies el signo de una desigualdad sumando o restando el mismo número entero en ambos lados de una ecuación.
Regla 2: suma o resta el mismo entero positivo de ambos lados de una ecuación de desigualdad.
Capítulo 7: Permutaciones y combinaciones
El presente capítulo explica los conceptos de permutación (una disposición de varios objetos en un orden definido) y combinación (una colección de objetos independientemente del orden). Los temas discutidos son el principio fundamental de conteo , factorial , permutaciones, combinaciones y sus aplicaciones junto con el concepto de permutación restringida . Si un determinado evento ocurre en ‘m’ formas diferentes seguido de un evento que ocurre en ‘n’ formas diferentes, entonces el número total de ocurrencias de los eventos se puede dar en orden m × n. Encuentre las fórmulas matemáticas importantes para la clase 11 Las permutaciones y combinaciones son las siguientes:
- Factorial : El producto continuo del primer n número natural se llama factorial ‘n’. Se denota por n! que está dado por,
¡norte! = n(n – 1)(n – 2)… 3 × 2 × 1 y 0! = 1! = 1
- Permutaciones : la permutación se refiere a los diversos arreglos que se pueden construir tomando algunas o todas las cosas de un conjunto. El número de un arreglo de n objetos tomados r a la vez, donde 0 < r ≤ n, denotado por n P r está dado por
norte PAG r = norte! / (n−r)!
- El número de permutaciones de n objetos de los cuales p 1 son de un tipo, p 2 son de segundo tipo,… pk son de k-ésimo tipo tal que p 1 + p 2 + p 3 + … + p k = n es
¡norte! / pág . 1 ! pág . 2 ! pág . 3 ! ….. pk !
- Combinaciones : Las combinaciones son cualquiera de las diversas selecciones formadas al tomar algunos o todos los objetos, independientemente de su disposición. El número de r objetos elegidos de un conjunto de n objetos está indicado por n C r , y viene dado por
norte C r = norte ! / r!(n−r)!
- Relación entre permutación y combinación: la relación entre los dos conceptos viene dada por dos teoremas como,
- norte PAG r = norte C r r! cuando 0 < r ≤ n.
- norte C r + norte C r-1 = n+1 C r
Capítulo 8: Teorema del binomio
Este capítulo analiza el teorema del binomio para números enteros positivos que se utiliza para resolver cálculos complejos. Los temas discutidos son la historia, el enunciado y la prueba del teorema del binomio y su expansión junto con el triángulo de Pascal . Un teorema del binomio ayuda a desarrollar un binomio dado para cualquier número entero positivo n.
- Teorema del binomio : La expansión de un binomio para cualquier número entero positivo n viene dada por el Teorema del binomio, que es
(a + b) norte = norte C 0 un norte + norte C 1 un norte-1 segundo + norte C2 un norte-2 segundo 2 + … + norte C norte -1 ab n -1 + norte C norte segundo norte
- Algunos casos especiales del teorema del binomio se pueden escribir como:
- (x – y) norte = norte C 0 x norte – norte C 1 x n -1 y + norte C 2 x n-2 y 2 + … + (-1) norte norte C norte x norte
- (1 – x) norte = norte C 0 – norte C 1 x + norte C 2 x 2 – …. (-1) norte norte C norte x norte
- norte C 0 = norte C norte = 1
- Triángulo de Pascal : Los coeficientes de las expansiones están ordenados en una array llamada triángulo de Pascal.
- Las Condiciones Generales de las siguientes ampliaciones son:
- (a + b) norte es T r +1 = norte C r un norte−r .b r
- (a – b) n es (-1) r n C r a n−r .b r
- (1 + x) norte = norte C r . x r
- (1 – x) norte = (-1) r norte C norte x r
- Términos medios : en la expansión (a + b) n , si n es par, entonces el término medio es el (n/2 + 1) enésimo término. Si n es impar, entonces los términos medios son (n/2 + 1) th y ((n+1)/2+1) th términos.
Capítulo 9: Secuencias y Series
El capítulo Secuencias y series analiza los conceptos de secuencia (una lista ordenada de números) y serie (la suma de todos los términos de una secuencia). Los temas discutidos son secuencia y serie, aritmética y progresión geométrica , aritmética y media geométrica. Aquí está la lista de algunos términos importantes utilizados en Secuencia y Serie que se enumeran a continuación:
- Progresión: Una secuencia cuyos términos siguen ciertos patrones se conoce como progresión.
- Progresión aritmética (AP) : una progresión aritmética (AP) es una secuencia en la que los términos aumentan o disminuyen regularmente por la misma constante. Esta constante se llama diferencia común (d). El primer término se denota por a y el último término de un AP se denota por l.
- Para una serie aritmética : a, a+d, a+2d, a+3d, a+4d, …….a +(n-1)d
- El primer término: a 1 = a,
- El segundo término: a 2 = a + d,
- El tercer término: a 3 = a + 2d,
- El enésimo término: a n = a + (n – 1)d
- El n-ésimo término de un AP desde el último término es a’ n =a n – (n – 1)d.
- a n + a’ n = constante
- Diferencia común de un AP es decir, d = a n – a n-1 , ∀ n>1.
- Suma de n Términos de un AP : S n = n/2 [2a + (n – 1)d] = n/2 (a 1 + a n )
- Una secuencia es un AP si la suma de n términos es de la forma An 2 + Bn, donde A y B son constantes y A = la mitad de la diferencia común, es decir, 2A = d.
un norte =S norte – S norte-1
- Media aritmética : si a, A y b están en AP entonces A = (a+b)/2 se llama la media aritmética de a y b. Si a 1 , a 2 , a 3 ,…… an son n números, entonces su media aritmética está dada por:
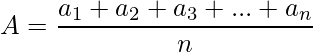
- La diferencia común se da como, d = (b – a)/(n + 1)
- La Suma de n media aritmética entre a y b es, n (a+b/2).
- Progresión geométrica (PG) : Una sucesión en la que la razón de dos términos consecutivos es constante se llama progresión geométrica.
- La razón constante se llama razón común (r).
es decir, r = un norte +1/un norte, ∀ n> 1- El término general o término n de GP es un n =ar n-1
- El enésimo término de un GP desde el final es a’ n = 1/r n-1 , l = último término
- Si a, byc son tres términos consecutivos de un GP entonces b 2 = ac.
- Media Geométrica (GM): Si a, G y b están en GR entonces G se llama la media geométrica de a y b y está dada por G = √(ab).
- Si a,G 1 , G 2 , G 3 ,….. G n , b están en GP entonces G 1 , G 2 , G 3 ,……G n están en GM entre a y b, entonces
la razón común es:- Si a 1 , a 2 , a 3 ,…, an son n números distintos de cero y no negativos, entonces su GM viene dado por GM
= (a 1 . a 2 . a 3 …a n ) 1/n- El producto de n GM es G 1 × G 2 × G 3 ×… × G n = G n = (ab) n/2
- La suma de los primeros n números naturales es: Σn = 1 + 2 + 3 +… + n = n(n+1)/2
- La suma de los cuadrados de los primeros n números naturales es: Σn 2 = 1 2 + 2 2 + 3 2 + … + n 2 = n(n+1)(2n+1)/6
- La suma de los cubos de los primeros n números naturales es: Σn 3 = 1 3 + 2 3 + 3 3 + .. + n 3 = (n(n+1)(2n+1)/6) 2
Capítulo 10: Líneas rectas
Las líneas rectas definieron el concepto de línea, su ángulo, pendiente y ecuación general. Los temas discutidos son la pendiente de una línea, el ángulo entre dos líneas, varias formas de ecuaciones de línea, la ecuación general de una línea y la familia de líneas, respectivamente. Aquí hay algunas fórmulas importantes usadas en el Capítulo Líneas rectas:
- Fórmula de distancia : La distancia entre dos puntos A(x 1 , y 1 ) y B (x 2 , y 2 ) viene dada por,
- La distancia de un punto A(x, y) al origen 0 (0, 0) viene dada por OA = √(x 2 + y 2 ).
- Fórmula de la sección : Las coordenadas del punto que divide el conjunto de (x 1 , y 1 ) y (x 2 , y 2 ) en la razón m:n internamente, es
Y externamente es:
- El punto medio de la unión de (x 1 , y 1 ) y (x 2 , y 2 ) es:
.
- El eje X divide el segmento de línea que une (x 1 , y 1 ) y (x 2 , y 2 ) en la razón -y 1 : y 2 .
- El eje Y divide el segmento de línea que une (x 1 , y 1 ) y (x 2 , y 2 ) en la razón -x 1 : x 2 .
- Las coordenadas del baricentro de un triángulo con vértices (x 1 , y 1 ), (x 2 , y 2 ) y (x 3 , y 3 ) son
- Área del Triángulo: El área del triángulo, las coordenadas de cuyos vértices son (x 1 , y 1 ), (x 2 , y 2 ) y (x 3 , y 3 ) es,
- Si los puntos (x 1 , y 1 ), (x 2 , y 2 ) y (x 3 , y 3 ) son colineales, entonces x 1 (y 2 – y 3 ) + x 2 (y 3 – y 1 ) + x 3 (y 1 – y 2 ) = 0 .
- Pendiente o gradiente de línea : la inclinación del ángulo θ a una línea con una dirección positiva del eje X en el sentido contrario a las agujas del reloj, la tangente del ángulo θ se dice que es la pendiente o gradiente de la línea y se denota por mie
m = tan θ
- La pendiente de una recta que pasa por los puntos P(x 1 , y 1 ) y Q(x 2 , y 2 ) viene dada por,
- Ángulo entre dos rectas: El ángulo θ entre dos rectas que tienen pendiente m 1 y m 2 es,
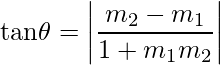
- Si dos líneas son paralelas, sus pendientes son iguales, es decir, m 1 = m 2 .
- Si dos líneas son perpendiculares entre sí, entonces su producto de pendientes es -1, es decir, m 1 m 2 = -1.
- Punto de intersección de dos rectas: Sea la ecuación de las rectas ax 1 + by 1 + c 1 = 0 y a 2 x + b 2 y + c 2 = 0, entonces su punto de intersección es
- Distancia de un punto a una recta: La distancia perpendicular de un punto P(x 1 , y 1 ) a la recta Ax + By + C = 0 viene dada por,
- Distancia entre dos rectas paralelas: La distancia d entre dos rectas paralelas y = mx + c 1 y y = mx + c 2 está dada por,
- Diferentes formas de Ecuación de una recta:
- Si una línea está a una distancia k y es paralela al eje X, entonces la ecuación de la línea es y = ± k.
- Si una línea es paralela al eje Y a una distancia de c del eje Y, entonces su ecuación es x = ± c.
- Ecuación general de una línea: cualquier ecuación de la forma Ax + By + C = 0 , donde A y B no son cero al mismo tiempo, se denomina ecuación general de una línea.
- Forma normal: La ecuación de una recta en la que la longitud de la perpendicular desde el origen es p y el ángulo formado por esta perpendicular al eje x es α, viene dada por: x cos α + y sen α = p.
- Forma de intersección: La ecuación de una recta que corta las intersecciones a y b respectivamente en los ejes x e y está dada por: x/a + y/b = 1.
- Forma pendiente-intersección : La ecuación de la línea con pendiente m y que hace una intersección c en el eje y, es y = mx + c.
- Forma de un punto-pendiente: La ecuación de una recta que pasa por el punto (x 1 , y 1 ) y tiene la pendiente m está dada por y – y 1 = m (x – x 1 ).
- Forma dos puntos: La ecuación de una recta que pasa por los puntos (x 1 , y 1 ) y (x 2 , y 2 ) viene dada por
Capítulo 11: Secciones cónicas
Los temas discutidos en el capítulo Secciones cónicas son las secciones de un cono, el caso degenerado de una sección cónica a lo largo de las ecuaciones y propiedades de las secciones cónicas. Un círculo es una figura geométrica donde todos los puntos en un plano están ubicados equidistantes del punto fijo en un plano dado. A continuación se encuentra la lista de algunas fórmulas importantes discutidas en el capítulo Secciones cónicas como,
- La ecuación de un círculo de radio r con centro (h, k) viene dada por (x – h) 2 + (y – k) 2 = r 2 .
- La ecuación general de la circunferencia viene dada por x 2 + y 2 + 2gx + 2fy + c = 0 , donde g, f y c son constantes.
- El centro del círculo es (-g, -f).
- El radio del círculo es r = √(g 2 + f 2 − c)
- La ecuación paramétrica del círculo x 2 + y 2 = r 2 viene dada por x = r cos θ, y = r sin θ , donde θ es el parámetro.
- Y la ecuación paramétrica del círculo (x – h) 2 + (y – k) 2 = r 2 viene dada por x = h + r cos θ, y = k + r sin θ.
- Parábola : Una parábola es el conjunto de puntos P cuyas distancias desde un punto fijo F en el plano son iguales a su distancia desde una línea fija l en el plano. El punto fijo F se llama foco y la recta l es la directriz de la parábola.
Diferentes formas de parábola.
y2 = 4ax
y2 = -4ax
x 2 = 4 días
x 2 = -4 día
eje de parábola
y = 0
y = 0
x = 0
x = 0
directriz de parábola
x = -a
x = un
y = -a
y = un
Vértice
(0, 0)
(0, 0)
(0, 0)
(0, 0)
Enfoque
(un, 0)
(-a, 0)
(0, un)
(0, -a)
Longitud del latus rectum
4a
4a
4a
4a
Longitud focal
|x + a|
|x – un|
|y + a|
|y – un|
- Elipse : Una elipse es el conjunto de todos los puntos del plano cuyas distancias a un punto fijo del plano guardan una razón constante, menor que a su distancia a un punto fijo del plano. El punto fijo se llama foco, la línea fija directriz y la relación constante (e) la excentricidad de la elipse. Las dos formas estándar de elipse con sus terminologías se mencionan a continuación en la tabla:
Diferentes formas de elipse
x 2 /a 2 + y 2 /b 2 = 1, a > b
x 2 /b 2 + y 2 /a 2 = 1, a > b
Ecuación del Eje Mayor
y = 0
x = 0
Longitud del eje mayor
2a
2a
Ecuación del Eje Menor
x = 0
y = 0
Longitud del eje menor
2b
2b
Ecuación de la Directriz
x = ±a/e
y = ±a/e
Vértice
(±a, 0)
(0, ±a)
Enfoque
(±ae, 0)
(0, ±ae)
Longitud del latus rectum
2b 2 / un
2b 2 / un
- Hipérbola : Una hipérbola es el lugar geométrico de un punto en un plano que se mueve de tal manera que la relación entre su distancia desde un punto fijo en el mismo plano y su distancia desde una línea fija es siempre constante, que siempre es mayor que la unidad. El punto fijo se llama foco, la recta fija se llama directriz y la razón constante, generalmente denotada por e, se conoce como excentricidad de la hipérbola. Las dos formas estándar de hipérbola con sus terminologías se mencionan a continuación en la tabla:
Diferentes formas de hipérbola
x2 / a2 – y2 / b2 = 1
x2 / a2 – y2 / b2 = 1
coordenadas del centro
(0, 0)
(0, 0)
Coordenadas de vértices
(±a, 0)
(0, ±a)
Coordenadas de focos
(±ae, 0)
(0, ±ae)
Longitud del eje conjugado
2b
2b
Longitud del eje transversal
2a
2a
Ecuación del eje conjugado
x = 0
y = 0
Ecuación del eje transversal
y = 0
x = 0
Ecuación de la Directriz
x = ±a/e
y = ±a/e
Excentricidad (e)
√(a 2 +b 2 )/a 2
√(a 2 +b 2 )/a 2
Longitud del latus rectum
2b 2 / un
2b 2 / un
Capítulo 12: Introducción a la geometría tridimensional
Como sugiere el nombre, el capítulo explica los conceptos de geometría en el espacio tridimensional. Los temas tratados son los ejes de coordenadas y planos respectivamente, coordenadas de puntos, distancia y sección para puntos. Los tres planos determinados por el par de ejes se conocen como planos de coordenadas con planos XY, YZ y ZX. Encuentre a continuación las fórmulas matemáticas importantes para la clase 11 Introducción a la geometría tridimensional como:
- Ejes de coordenadas : en tres dimensiones, los ejes de coordenadas de un sistema de coordenadas cartesiano rectangular son tres líneas perpendiculares entre sí. Estos ejes se denominan ejes X, Y y Z.
- Planos de coordenadas : Los tres planos determinados por el par de ejes son los planos de coordenadas. Estos planos se denominan planos XY, YZ y ZX y dividen el espacio en ocho regiones conocidas como octantes.
- Coordenadas de un punto en el espacio: Las coordenadas de un punto en el espacio son las distancias perpendiculares desde P en tres planos de coordenadas mutuamente perpendiculares YZ, ZX y XY respectivamente. Las coordenadas de un punto P se escriben en forma de triplete como (x, y, z). Las coordenadas de cualquier punto en:
- El eje X tiene la forma (x, 0,0)
- El eje Y tiene la forma (0, y, 0)
- El eje Z tiene la forma (0, 0, z)
- El plano XY tiene la forma (x, y, 0)
- El plano YZ tiene la forma (0, y, z)
- El plano ZX tiene la forma (x, 0, z)
- Fórmula de distancia: La distancia entre dos puntos A(x 1 , y 1 , z 1 ) y B(x 2 , y 2 , z 2 ) está dada por,
- Mientras que la distancia entre dos puntos A(x, y, z) desde el origen O(0, 0, 0) viene dada por,
- Fórmula de la sección : Las coordenadas del punto R que divide el segmento de recta que une dos puntos P(x 1 , y 1 , z 1 ) y Q(x 2 , y 2 , z 2 ) interna o externamente en la relación m : n son dada por,
- El punto medio de la articulación de (x 1 , y 1 ) y (x 2 , y 2 ) es:
- Las coordenadas del baricentro de un triángulo con vértices (x 1 , y 1 ), (x 2 , y 2 ) y (x 3 , y 3 ) son
Capítulo 13: Límites y Derivadas
El capítulo explica el concepto de cálculo que se ocupa del estudio del cambio en el valor de una función cuando el cambio ocurre en los puntos del dominio. Los temas tratados son la definición y operaciones algebraicas de límites y derivadas respectivamente.
Un límite de una función en un cierto punto tiene un valor común de los límites izquierdo y derecho si coinciden entre sí. Aquí está la lista de algunas fórmulas importantes que se utilizan para resolver problemas de Límites y Derivadas como,
- Límite : Sea y = f(x) una función de x. Si en x = a, f(x) toma forma indeterminada, entonces consideramos los valores de la función que está muy cerca de a. Si estos valores tienden a un número único definido como x tiende a a, entonces el número único así obtenido se llama límite de f(x) en x = a y lo escribimos como
.
- Límites izquierdo y derecho: si los valores de la función en el punto que está muy cerca de a a la izquierda tienden a un número único definido cuando x tiende a a, entonces el número único así obtenido se denomina límite izquierdo. de f(x) en x = a, lo escribimos como
- De manera similar, el límite de la mano derecha se da como,
- Existe un límite
cuando:
y
ambos existen o,
- Algunas propiedades importantes de los límites : Considere que f y g son dos funciones tales que existen tanto \lim_{x\to a}f(x) como \lim_{x\to a}g(x), entonces:
- Algunos límites estándar se dan como:

- Derivadas : Considere una función de valor real f, tal que:

se conoce como la derivada de la función f en x si y solo si,
existe finitamente.
- Algunas propiedades importantes de las derivadas: Considere que f y g son dos funciones tales que sus derivadas se pueden definir en un dominio común como:
- Algunas Derivadas Estándar se dan como:
Capítulo 14: Razonamiento matemático
Como sugiere el nombre, el capítulo explica los conceptos del razonamiento matemático (una habilidad crítica para analizar cualquier hipótesis dada en el contexto de las matemáticas). Los temas discutidos son declaraciones, razonamiento inductivo y razonamiento deductivo. La siguiente es la lista de términos importantes discutidos como:
- Declaraciones : Una declaración es una oración que es verdadera o falsa, pero no ambas simultáneamente. Por ejemplo: “Un triángulo tiene cuatro lados”, “Nueva Delhi es la capital de la India”. son las declaraciones.
- Negación de un enunciado : Negación de un enunciado p: Si p denota un enunciado, entonces la negación de p se denota por ∼p.
- Declaración compuesta : una declaración es una declaración compuesta si se compone de dos o más declaraciones más pequeñas. Los enunciados más pequeños se denominan enunciados componentes del enunciado compuesto. Las declaraciones compuestas son hechas por:
- Conectivos : “Y”, “O”
- Cuantificadores : “existe”, “Para cada”
- Implicaciones: El significado de las implicaciones “si”, “solo si”, “si y solo si”.
- “p ⇒ q” :
- p es una condición suficiente para q o p implica q.
- q es necesario condicionar para p. El recíproco de un enunciado p ⇒ q es el enunciado q ⇒ p.
- p⇒ q junto con su inversa da p si y solo si q.
- “p ⇔ q”:
- p implica q (denotado por p ⇒ q)
- p es una condición suficiente para q
- q es una condición necesaria para p
- p solo si q
- ∼q implica ∼p
- Contrapositivo : El contrapositivo de un enunciado p ⇒ q es el enunciado ∼ q ⇒∼p.
- Contradicción: Si para comprobar si p es verdadera asumimos que la negación p es verdadera.
- Validación de enunciados : Comprobación de un enunciado si es verdadero o falso. La validez de una declaración depende de cuál de las especiales. Los siguientes métodos se utilizan para verificar la validez de las declaraciones:
- método directo
- método contrapositivo
- método de contradicción
- utilizando un contraejemplo.
Capítulo 15: Estadísticas
Este capítulo explica los conceptos de estadística (datos recopilados para propósitos específicos), dispersión y métodos de cálculo para datos agrupados y no agrupados. Los temas discutidos son rango, desviación media, varianza y desviación estándar , y análisis de distribuciones de frecuencia . Aquí encontrará las fórmulas matemáticas esenciales para la Clase 11 de Estadística que se detallan a continuación:
- Medida de Dispersión : La dispersión es la medida de variaciones en los valores de la variable. Mide el grado de dispersión de la observación en una distribución alrededor del valor central.
- Rango : La medida de dispersión más fácil de entender y de calcular es el rango. El rango se define como la diferencia entre dos observaciones extremas de la distribución.
Rango de distribución = Observación más grande – Observación más pequeña.
Desviación media para datos no agrupados: para n observaciones x 1 , x 2 , x 3 ,…, x n , la desviación media sobre su media x¯ viene dada por:
Y, la desviación media sobre su mediana M está dada por,
Desviación media para distribución de frecuencia discreta-
Varianza : La varianza es la media aritmética del cuadrado de la desviación respecto a la media x¯.
Sean x 1 , x 2 , ……x n n observaciones con x¯ como media, entonces la varianza denotada por σ 2 , está dada por
Desviación estándar : si σ 2 es la varianza, entonces σ se llama la desviación estándar viene dada por
La desviación estándar de una distribución de frecuencia discreta viene dada por
Coeficiente de variación: Para comparar dos o más distribuciones de frecuencia, comparamos su coeficiente de variación. El coeficiente de variación se define como
Coeficiente de variación = (Desviación estándar / Media) × 100
Capítulo 16: Probabilidad
La probabilidad es una parte fundamental del plan de estudios de Matemáticas de Clase 11 y es importante para los exámenes de Clase 11 y diferentes exámenes competitivos como JEE y NEET. En clases anteriores, los estudiantes pueden haber aprendido el concepto básico de probabilidad como una medida de incertidumbre de varios fenómenos. Aquí se analiza una lista de fórmulas, propiedades importantes, aplicaciones y un resumen del capítulo, lo que ayudará a los estudiantes a aprender rápidamente los conceptos relacionados y obtener buenas calificaciones en el examen.
El capítulo analiza el concepto de probabilidad (una medida de la incertidumbre de varios fenómenos o la posibilidad de que ocurra un evento). Los temas discutidos son los experimentos aleatorios , los resultados, los espacios muestrales, el evento y su tipo . A continuación se muestra la lista de fórmulas importantes y el resumen del capítulo para la probabilidad de Clase 11 como:
- Probabilidad = Número de resultados favorables en un evento / Número total de resultados
- Evento : Un evento es un subconjunto del S (espacio muestral). Un conjunto vacío también se conoce como el evento Imposible.
- Para cualquier experimento aleatorio , sea S el espacio muestral. La probabilidad P es una función de valor real cuyo dominio es el conjunto potencia de S y [0, 1] es el intervalo de rango. Para cualquier evento E: P(E) ≥ 0 y P(S) = 1
- Eventos mutuamente excluyentes : Si E y F son eventos mutuamente excluyentes, entonces: P(E ∪ F) = P(E) + P(F)
- Resultados igualmente probables: todos los resultados con la misma probabilidad se denominan resultados igualmente probables. Sea S un espacio muestral finito con resultados igualmente probables y A el evento. Por lo tanto, la probabilidad de un evento A es: P(A) = n(A) / n(S), donde n(A) es el número de elementos del conjunto A y n(S) es el número total de resultados o el número de elementos en el espacio muestral S
- Sean P y Q dos eventos cualquiera, entonces se pueden derivar las siguientes fórmulas.
- Evento P o Q: El conjunto P ∪ Q
- Evento P y Q: El conjunto P ∩ Q
- Evento P y no Q: El conjunto P – Q
- P y Q son mutuamente excluyentes si P ∩ Q = φ
- Eventos P 1 , P 2 , . . . . . , P n son exhaustivos y mutuamente excluyentes si P 1 ∪ P 2 ∪ . . . . . ∪ PAGS n = S y mi yo ∩ mi j = φ para todo i ≠ j.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
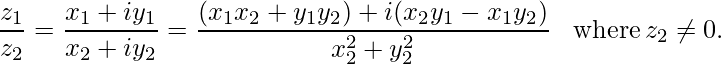
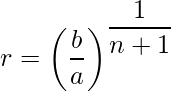
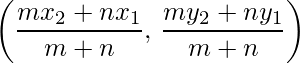
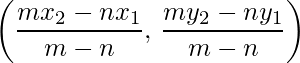
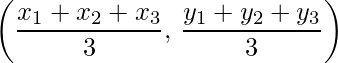
![Rendered by QuickLaTeX.com \begin{aligned}\text{Area of Triangle}&=\dfrac{1}{2}\begin{vmatrix}x_1&x_2&1\\x_2&y_2&1\\x_3&x_2&1\end{vmatrix}\\&=\dfrac{1}{2}\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right]\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a4aeb7acecdfe4c3fe0235a0b920c1f_l3.png)
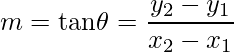
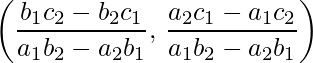
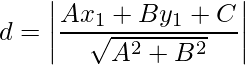
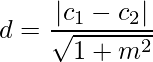
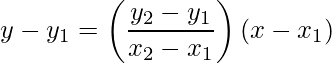
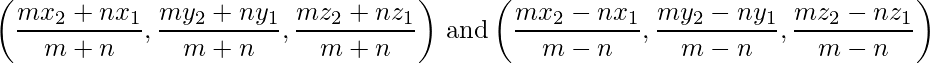

![Rendered by QuickLaTeX.com \begin{aligned}\lim_{x\to a}[f(x)\pm g(x)]&=\lim_{x\to a}f(x)\pm \lim_{x\to a} g(x)\\\lim_{x\to a}kf(x)&=k\lim_{x\to a}f(x)\\\lim_{x\to a}f(x)\cdot g(x)&=\lim_{x\to a}f(x)\times\lim_{x\to a}g(x)\\\lim_{x\to a}\dfrac{f(x)}{g(x)}&=\dfrac{\lim_{x\to a}f(x)}{\lim_{x\to a}g(x)}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f79d4730e45e635c86c80ba858728930_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)+g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]+\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)-g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]-\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)\cdot g(x)]&=\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)+f(x)\cdot\left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]\\\dfrac{\mathrm{d}}{\mathrm{d}x}\left[\dfrac{f(x)}{g(x)}\right]&=\dfrac{\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)-f(x)\cdot \left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]}{[g(x)]^2}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-deffb33d9df811e455f522770076822d_l3.png)