La Junta Central de Educación Secundaria (CBSE, por sus siglas en inglés) realizó el examen de la Junta de Matemáticas de la Clase 12 del Término 1 2021-22 el lunes 6 de diciembre de 2021. El trabajo fue calificado como largo y difícil según lo declarado por los estudiantes.
Discutamos la estructura del CBSE Class 12 Maths Term 1 Question Paper 2021.
El cuestionario consta de 50 preguntas divididas en las secciones A, B y C en las que la Sección:
- A consta de 20 preguntas de 1 punto cada una. Los estudiantes deben intentar 16 preguntas,
- B consta de 20 preguntas de 1 punto cada una. Los estudiantes deben intentar 16 preguntas,
- C consta de 10 preguntas de 1 punto cada una. Solo se necesitan ocho preguntas para intentarlo.
La sección A evaluó el conocimiento y la comprensión de los estudiantes, donde algunas preguntas requirieron pequeños cálculos. La Sección B fue desafiante, requirió que los estudiantes tuvieran una comprensión completa de las ideas para poder responder los problemas. Las preguntas de programación lineal toman mucho tiempo para responder. La sección C evaluó la capacidad de los estudiantes para aplicar sus conocimientos. Esta parte parece ser difícil de aprobar para un estudiante promedio.
Ahora, analicemos el CBSE Class 12 Maths Term 1 Paper Series SSJ / 1 – Set 4 para 2021 con las claves de respuesta y sus soluciones del Class 12 Maths Paper.
El capítulo ‘ Aplicaciones de derivadas ‘ obtuvo la mayor cantidad de puntos y preguntas, seguido de ‘ Arrays ‘ y ‘ Relaciones y funciones ‘. El menor número de preguntas se hizo de ‘ Determinantes ‘ y ‘ Funciones trigonométricas inversas ‘. Solo hay una pregunta de estudio de caso en ‘Aplicaciones de derivados.
La sección A fue fácil, la sección B fue muy compleja y la sección C fue relativamente fácil pero requirió mucho tiempo, además, la pregunta 42 de la sección C tenía símbolos que no estaban presentes en los libros de texto del NCERT . Por lo tanto, se destaca que ciertas preguntas requerían que los estudiantes pensaran creativamente y que los problemas de estudio de caso requerían buenas habilidades de pensamiento. Por lo tanto, el examen de Matemáticas del Término 1 de CBSE de 2021 fue moderadamente difícil y requirió mucho tiempo, y ciertas preguntas requirieron tiempo adicional para responder.
Aquí, el documento de preguntas resueltas (junto con las respuestas y la explicación detallada de cada pregunta) del examen de Matemáticas CBSE Class 12th Term 1 se proporciona como:
CBSE Class 12th Term 1 Math Board Examen Preguntas y respuestas Clave 2021-22 (SET 4)
Asignatura- Matemáticas
Término- I
Tiempo permitido- 90 minutos
Marcas máximas: 40
Instrucciones generales
Lea atentamente las siguientes instrucciones y sígalas estrictamente:
- Este cuestionario contiene 50 preguntas, de las cuales 40 deben intentarse. Todas las preguntas llevan marcas iguales.
- El cuestionario consta de tres secciones: la sección A, B y C.
- Sección – A contiene 20 preguntas. Intente cualquiera de las 16 preguntas de la P. No. 01 a la 20.
- La sección B también contiene 20 preguntas. Intente cualquiera de las 16 preguntas de la P. No. 21 a la 40.
- La sección C contiene dos estudios de casos que contienen 5 preguntas en cada caso. Intente 4 preguntas cualesquiera de la P. N° 41 a la 45 y otras 4 de la P. N° 46 a la 50.
- Solo hay una opción correcta para cada pregunta de opción múltiple (MCQ). No se otorgarán puntos por responder más de una opción.
- No hay marca negativa.
SECCIÓN A
Las preguntas número 1 a 20 son de 1 punto cada una . Se necesita intentar 16 preguntas cualesquiera de la pregunta 1 a la 20 .
Pregunta 1: Diferencial de log [log (log x 5 )] wrt x es
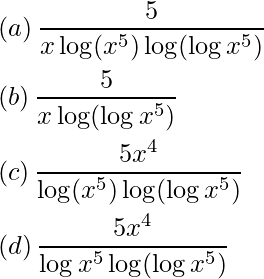
Respuesta: (a)
Pregunta 2: El número de todas las arrays posibles de orden 2 × 3 con cada entrada 1 o 2 es
(a) 16
(b) 6
c) 64
(d) 24
Respuesta: (c)
Pregunta 3: Una función f : R → R se define como f(x) = x³ + 1. Entonces la función tiene
(a) ningún valor mínimo
(b) ningún valor máximo
c) tanto los valores máximos como los mínimos
(d) ni valor máximo ni valor mínimo
Respuesta: (d)
Pregunta 4: Si sen y = x cos (a + y), entonces dx/dy es
(a) cos a/cos² (a+y)
(b) – cos a/cos² (a+y)
(c) cos a/sen² y
(d) – cos a/sen² y
Respuesta: (a)
Pregunta 5: Los puntos en la curva x²/9 + y²/25 + 1, donde la tangente es paralela al eje x son
(a) (±5, 0)
(b) (0, ±5)
(c) (0, ±3)
(d) (±3, 0)
Respuesta: (b)
Pregunta 6: Tres puntos P(2x, x + 3), Q(0, x) y R(x + 3, x + 6) son colineales, entonces x es igual a
(a) 0
(b) 2
(c) 3
(d) 1
Respuesta: (d)
Pregunta 7: El valor principal de 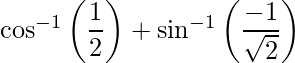 es
es
(a) π/12
(b) π
(c) π/3
(d) π/6
Respuesta: (a)
Pregunta 8: Si (x²+ y²)² = xy, entonces dy/dx es
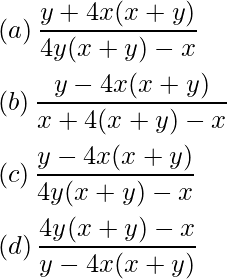
Respuesta: (c)
Pregunta 9: Si una array A es tanto simétrica como asimétrica, entonces A es necesariamente
(a) Array diagonal
(b) Array cuadrada cero
(c) Array cuadrada
(d) Array de identidad
Respuesta: (b)
Pregunta 10: Sea X = {1, 2, 3} y una relación R se define en X como: R = {(1, 3), (2, 2), (3, 2)}, entonces pares mínimos ordenados que deben agregarse en la relación R para hacerla reflexiva y simétrica son
(a) {(1, 1), (2, 3), (1, 2)}
(b) {(3, 3), (3, 1), (1, 2)}
(c) {(1, 1), (3, 3), (3, 1), (2, 3)}
(d) {(1, 1), (3, 3), (3, 1), (1, 2)}
Respuesta: (c)
Pregunta 11: Un problema de programación lineal es el siguiente:
Minimizar z = 2x + y
sujeto a las restricciones x ≥3 , x ≤9, y ≥ 0
x – y ≥ 0, x + y≤14
La región factible tiene
(a) 5 puntos de esquina incluidos (0, 0) y (9, 5)
(b) 5 puntos de esquina incluyendo (7. 7) y (3, 3)
(c) 5 puntos de esquina incluyendo (14, 0) y (9, 0)
(d) 5 puntos de esquina incluidos (3, 6) y (9, 5)
Respuesta: (b)
Pregunta 12: La función 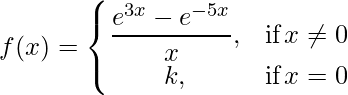 es continua en x = 0 para el valor de k como
es continua en x = 0 para el valor de k como
(a) 3
(b) 5
(c) 2
(d) 8
Respuesta: (d)
Pregunta 13: Si C ij denota el cofactor del elemento p ij de la array 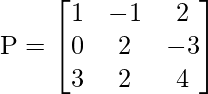 , entonces el valor de C 31 . C 23 es
, entonces el valor de C 31 . C 23 es
(a) 3
(b) 5
(c) 2
(d) 8
Respuesta: (a)
Pregunta 14: La función de y = x 2 e -x es decreciente en el intervalo
(a) (0, 2)
(b) (2, ∞)
(c) (-∞, 0)
(d) (-∞, 0) ∪ (2, ∞)
Respuesta: (d)
Pregunta 15: Si R= {(x, y); x, y ∈ z, x² + y² ≤ 4} es una relación en el conjunto Z, entonces el dominio de R es
(a) {0, 1, 2}
(b) {-2, -1, 0, 1, 2}
c) {0, -1, -2}
(d) {-1, 0, 1}
Respuesta: (b)
Pregunta 16: El sistema de ecuaciones lineales
5x + ky = 5,
3x + 3y = 5;
será consistente si
(a) k ≠ -3
(b) k = -5
c) k = 5
(d) k ≠ 5
Respuesta: (d)
Pregunta 17: La ecuación de la tangente a la curva y (1 + x 2 ) = 2 – x, donde cruza el eje x es
(a) x – 5y = 2
(b) 5x – y = 2
c) x + 5y = 2
(d) 5x + y = 2
Respuesta: (c)
Pregunta 18: Si 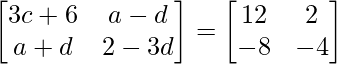 son iguales, entonces el valor de ab – cd es
son iguales, entonces el valor de ab – cd es
(un) 4
(b) 16
(c) -4
(d) -16
Respuesta: (a)
Pregunta 19: El valor principal de 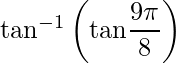 es
es
(a) π/8
(b) 3π/8
(c) -π/8
(d) -3π/8
Respuesta: (a)
Pregunta 20: Para dos arrays 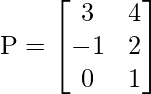 y
y 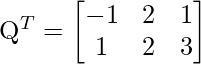 P – Q es
P – Q es
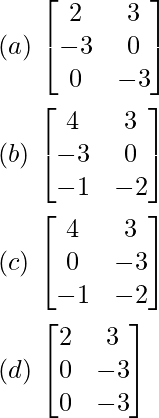
Respuesta: (b)
SECCIÓN B
En esta Sección, intente 16 preguntas de las Preguntas 21-40. Cada pregunta es de una nota.
Pregunta 21: La función f(x) = 2x 3 – 15x 2 + 36 x + 6 es creciente en el intervalo
(a) (∞, 2) ∪ (3, ∞)
(b) (-∞, 2)
(c) (-∞, 2) ∪ (3, ∞)
(d) (3, ∞)
Respuesta: (c)
Pregunta 22: Si x = 2 cosθ – cos 2θ y y = 2 senθ – sen 2θ, entonces dy/dx es
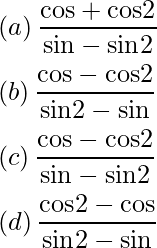
Respuesta: (b)
Pregunta 23: ¿Cuál es el dominio de la función cos -1 (2x – 3)?
(a) [-1, 1]
(b) (1, 2)
c) (-1, 1)
(d) [1, 2]
Respuesta: (d)
Pregunta 24: Una array A = [a ij ] 3 × 3 está definida por
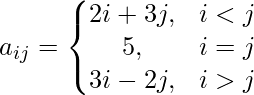
El número de elementos en A que son más de 5, es
(a) 3
(b) 4
c) 5
(d) 6
Respuesta: (b)
Pregunta 25: Si una función f definida por.
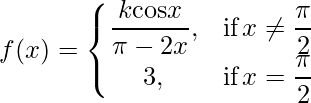
es continua en x = π/2 . entonces el valor de k es
(a) 2
(b)3
(c) 6
(d)-6
Respuesta: (c)
Pregunta 26: Para la array 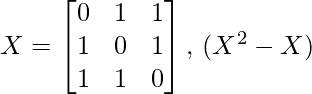 es
es
(a) 2I
(b) 3I
(c) yo
(d) 5I
Respuesta: (a)
Pregunta 27: Sea X = {x 2 : x ∈ N} y la función f : N → X está definida por f(x) = x 2 , x ∈ N. Entonces esta función es
(a) solo inyectable
(b) no biyectiva
(c) solo sobreyectiva
(d) biyectiva
Respuesta: (d)
Pregunta 28: Los puntos de esquina de la región factible para un problema de Programación Lineal son P(0, 5). Q(1, 5), R(4, 2) y S(12, 0). El valor mínimo de la función objetivo Z = 2x + 5y está en el punto
(a) P
(b) Q
(c)R
(d) S
Respuesta: (c)
Pregunta 29: La ecuación de la normal a la curva ay 2 = x 3 en el punto (am 2 , am 3 ) es
(a) 2y – 3mx + am 3 = 0
(b) 2x + 3my – 3am 4 – am 2 = 0
(c) 2x + 3my + 3am 4 – 2am 2 = 0
(d) 2x + 3my – 3am 4 – 2am 2 = 0
Respuesta: (d)
Pregunta 30: Si A es una array cuadrada de orden 3 y | un | = -5, entonces | adj A | es
(a) 125
(b) – 25
c) 25
(d) ± 25
Respuesta: (c)
Pregunta 31: La forma más simple de 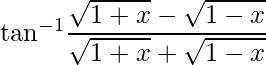 es
es
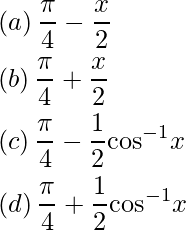
Respuesta: (c)
Pregunta 32: Si para la array 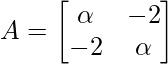 , | Un 3 | =125, entonces el valor de α es
, | Un 3 | =125, entonces el valor de α es
(a) ±3
(b) -3
c) ±1
(d) 1
Respuesta: (a)
Pregunta 33: Si y = sen (m sen -1 x), ¿cuál de las siguientes ecuaciones es verdadera?
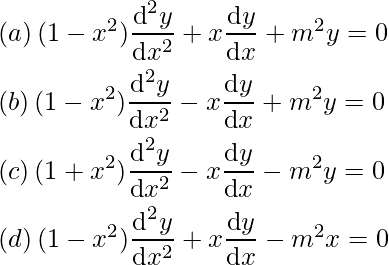
Respuesta: (b)
Pregunta 34: El valor principal de [tan -1 √3 – cot -1 (-√3)] es
(a) π
(b) -π/2
(c) 0
(d) 2√3
Respuesta: (b)
Pregunta 35: El valor máximo de 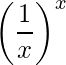 es
es
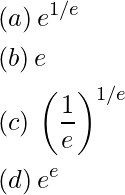
Respuesta: (a)
Pregunta 36: Sea la array X = [x ij ] dada por  , Entonces la array Y = [m ij ] = Menor de x ij es
, Entonces la array Y = [m ij ] = Menor de x ij es

Respuesta: (d)
Pregunta 37: Una función f : R ⇢ R definida por f(x) = 2 + x 2 es
(a) no uno-uno
(b) uno-uno
(c) no sobre
(d) ni uno ni sobre
Respuesta: (d)
Pregunta 38: Un problema de programación lineal es el siguiente:
Maximizar/Minimizar función objetivo Z = 2x – y + 5
Sujeto a las restricciones
3x + 4y ≤ 60
x + 3y ≤ 30
x ≥ 0, y ≥ 0
Si los puntos de esquina de la región factible son A (0, 10), B (12, 6), C (20, 0) y O (0, 0), ¿cuál de los siguientes es verdadero?
(a) El valor máximo de Z es 40
(b) El valor mínimo de Z es – 5
(c) La diferencia de los valores máximo y mínimo de Z es 35
(d) En dos puntos de esquina, el valor de Z es igual
Respuesta: (b)
Pregunta 39: Si x = -4 es raíz de 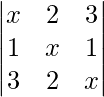 , entonces la suma de las otras dos raíces es
, entonces la suma de las otras dos raíces es
(un) 4
(b) -3
(c) 2
(d) 5
Respuesta: (a)
Pregunta 40: El valor máximo absoluto de la función f(x) = 4x – 1/2 x 2 en el intervalo [-2, 9/2] es
(a) 8
(b) 9
(c) 6
(d) 10
Respuesta: (a)
SECCIÓN – C
Intente 8 preguntas cualesquiera de las Preguntas 41-50. Cada pregunta es de una nota.
Cuestión 41: En una esfera de radio r se inscribe un cono circular recto de altura h de máxima superficie curva. La expresión para el cuadrado de la superficie curva del cono es
(a) 2πr 2 rh (2rh + h 2 )
(b) π 2 h (2rh + h 2 )
(c) 2π 2 r (2rh 2 – h 3 )
(d) 2π 2 r 2 (2rh – h 2 )
Respuesta: (c)
Pregunta 42: Los puntos de esquina de la región factible determinados por un conjunto de restricciones (desigualdades lineales) son P(0, 5), Q(3, 5), R(5, 0) y S(4, 1) y el la función objetivo es Z = ax + 2by donde a, b > 0. La condición en a y b tal que el máximo Z ocurre en Q y S es
(a) a – 5b = 0
(b) a – 3b = 0
(c) a – 2b = 0
(d) a – 8b = 0
Respuesta: (d)
Pregunta 43: Si la curva y 2 = 4x y xy = c cortan en ángulo recto, entonces el valor de c es
(a) 4√2
(b) 8
c) 2√2
(d) -4√2
Respuesta: (a)
Pregunta 44: la inversa de la array 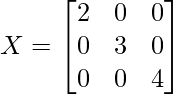 es
es
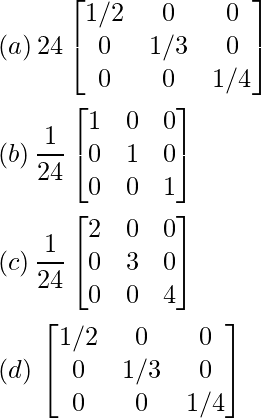
Respuesta: (d)
Pregunta 45: Para un LPP, la función objetivo es Z = 4x + 3y, y la región factible determinada por un conjunto de restricciones (inecuaciones lineales) se muestra en el gráfico.

¿Cuál de las siguientes afirmaciones es verdadera?
(a) El valor máximo de Z está en R.
(b) El valor máximo de Z está en Q.
(c) El valor de Z en R es menor que el valor en P.
(d) El valor de Z en Q es menor que el valor en R.
Respuesta: (b)
Caso de estudio
En una sociedad residencial compuesta por 100 casas, había 60 niños de entre 10 y 15 años. Fueron inspirados por sus maestros para comenzar a hacer composta para garantizar que los desechos biodegradables se reciclen. Para ello, en lugar de que cada niño lo hiciera solo para su casa, los niños convencieron a la Asociación de Bienestar de los Vecinos para hacerlo como una iniciativa de la sociedad. Para ello , identificaron una plaza en el parque local. Las autoridades locales cobraron una cantidad de ₹ 50 por metro cuadrado por espacio para que no haya un mal uso del espacio y la asociación de bienestar de residentes lo tome en serio. La asociación contrató a un peón para excavar 250 m 3 y cobró ₹ 400 × (profundidad) 2 . A la asociación le gustaría tener un costo mínimo.
Con base en esta información, responda 4 de las siguientes preguntas.
Pregunta 46: Si el lado de la parcela cuadrada es xm y su profundidad es h metros, entonces el costo c para el pozo es
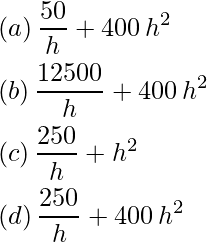
Respuesta: (b)
Pregunta 47: Valor de h (en m) para el cual dc/dh = 0 es
(un) 1,5
(b) 2
c) 2,5
(d) 3
Respuesta: (c)
Pregunta 48: d 2 c/dh 2 está dada por
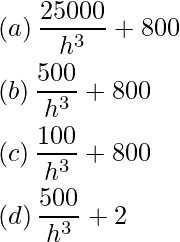
Respuesta: (a)
Pregunta 49: El valor de c (en m) para el costo mínimo es
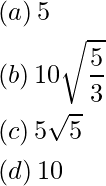
Respuesta: (d)
Pregunta 50: El costo mínimo total de excavar el pozo (en ₹) es
(a) 4.100
(b) 7.500
c) 7.850
d) 3.220
Respuesta: (b)
Publicación traducida automáticamente
Artículo escrito por mayurigrover y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA