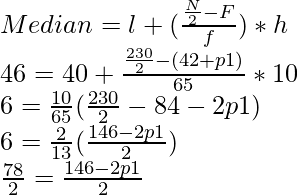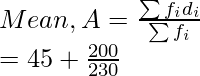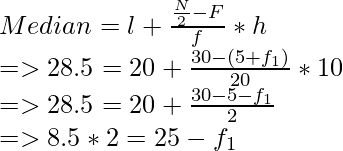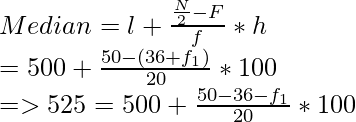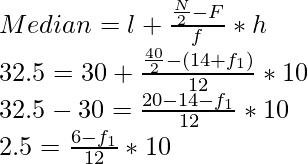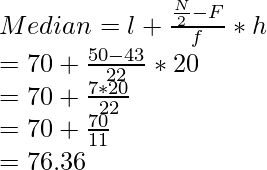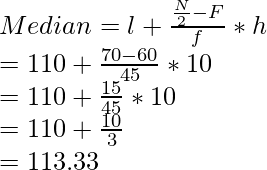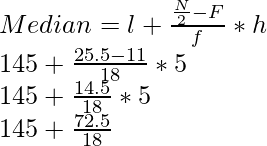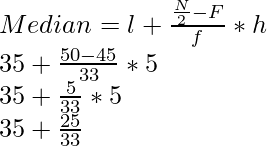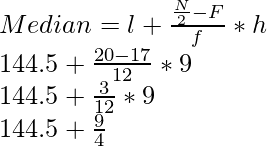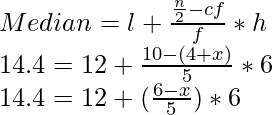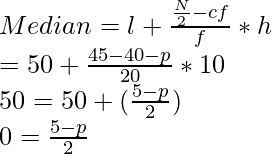Solución Clase 10 RD Sharma – Capítulo 7 Estadísticas – Ejercicio 7.4

Pregunta 11. A continuación se da una distribución incompleta:

Variable	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Frecuencia	12	30	–	sesenta y cinco	–	25	18

Se le da que el valor medio es 46 y el número total de elementos es 230.

(i) Utilizando la fórmula de la mediana, rellene las frecuencias que faltan.

(ii) Calcule el AM de la distribución completa.

Solución:

Supongamos que p1 y p2 son las frecuencias que faltan

Mediana = 46 y N = 230

Variable Frecuencia (f) cf

10-20 12 12

20-30 30 42

30-40 p1 42+p1

40-50 sesenta y cinco 107+p1

50-60 p2 107+p1+p2

60-70 25 132+p1+p2

70-80 18 150+p1+p2

Total 230

∴ 150 + p1 + p2 = 230

⇒ p1+p2 = 230 – 150 = 80

∴ p2 = 80-p1 …..(i)

Dado que mediana = 46 que se encuentra en el intervalo de clase perteneciente a 40-50

∴ I = 40, f= 65, F = 42 +p1, h = 10

$Mediana = l + (\frac{\frac{N}{2}-F}{f})*h \\ 46 = 40 + \frac{\frac{230}{2} - (42 + p1)}{ 65}*10 \\ 6 = \frac{10}{65}(\frac{230}{2} - 84 - 2p1) \\ 6 = \frac{2}{13}(\frac{146-2p1} {2}) \\ \frac{78}{2} = \frac{146 - 2p1}{2}$

⇒ 39 = 73 – p1

⇒ p1 = 73 -39 = 34

∴ p2 – 80 – p1 = 80 – 34 = 46

Por lo tanto, las frecuencias que faltan son 34 y 46.

Sea la media supuesta (A) 45.

Variable Marcas de clase (x) Frecuencia (f)
d = x-A

A = 45
f _i * d _i

10-20 15 12 -30 -360

20-30 25 30 -20 -600

30-40 35 34 -10 -340

40-50 45-A sesenta y cinco 0 0

50-60 55 46 10 460

60-70 sesenta y cinco 25 20 500

70-80 75 18 30 540

Total 230 200

$Media, A = \frac{\sum f_id_i}{\sum f_i} \\ = 45 + \frac{200}{230}$

= 45 + 0,8695

= 45 + 0,87

= 45,87

Pregunta 12. Si la mediana de la siguiente distribución de frecuencias es 28,5, encuentre las frecuencias que faltan:

Intervalo de clases	0-10	20-30	30-40	40-50	50-60	Total
Frecuencia	5	F ₁	15	F ₂	5	60

Solución:

Media = 28,5, N = 60

Intervalo de clases Frecuencia cf

0-10 5 5

10-20 F ₁ 5 + f ₁

20-30 20 25 + f ₁

30-40 15 40 + f ₁

40-50 F ₂ 40 + f ₁ + f ₂

50-60 5 45 + f ₁ + f ₂

Total 60

Por lo tanto,

45 + f ₁ + f ₂ = 60

=> f ₁ + f ₂ = 60 – 45 = 15

=> f ₂ = 15 – f ₁

17 = 25 – f ₁

N/2 = 30

Ahora, mediana = 28,5 y se encuentra en el intervalo de clase de 20-30

Por lo tanto,

l = 20, F = 5 + f ₁ , f = 20 y h = 10

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ => 28.5 = 20 + \frac{30 - (5+f_1)}{20} * 10 \\ => 28.5 = 20 + \frac{30-5-f_1}{2} \\ => 8.5 * 2 = 25 - f_1$

⇒ f ₁ = 25 -17 = 8

y f ₂ = 15-f ₁ = 15-8 = 7

Por lo tanto, las frecuencias que faltan son 8 y 7 respectivamente.

Pregunta 13. La mediana de los siguientes datos es 525. Encuentra la frecuencia que falta, si se da que hay 100 observaciones en los datos:

Intervalo de clases	Frecuencia	Intervalo de clases	Frecuencia
0-100	2	500-600	20
100-200	5	600-700	F ₂
200-300	F ₁	700-800	9
300-400	12	800-900	7
400-500	17	900-1000	4

Solución:

Mediana = 525, N = 100

Intervalo de clases Frecuencia cf

0-100 2 2

100-200 5 7

200-300 F ₁ 7 + f ₁

300-400 12 19 + f ₁

400-500 17 36 + f ₁

500-600 20 56 + f ₁

600-700 F ₂ 56 + f ₁ + f ₂

700-800 9 65 + f ₁ + f ₂

800-900 7 72 + f ₁ + f ₂

900-1000 4 76 + f ₁ + f ₂

Total 100

Por lo tanto,

76 + f ₁ + f ₂ = 100 => f ₁ + f ₂ = 100 – 76 = 26

f ₂ = 24 – f ₁

Porque,

Mediana = 525 que pertenece al intervalo 500-600

Ahora, l = 500, F = 36 + f ₁ , f = 20, h = 100

Por lo tanto,

METRO $Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 500 + \frac{50 - (36 + f_1)}{20} * 100 \\ => 525 = 500 + \frac{50-36-f_1}{20} * 100$

⇒ 525 – 500 = (14 -f ₁ ) x 5

⇒ 25 = 70- 5f ₁

⇒ 5f ₁ = 70 – 25 = 45

⇒ f1 ₌ 455 = 9

y f ₂ = 24 – f ₁ = 24 – 9 = 15

Por lo tanto, obtenemos los valores para f ₁ = 9, f ₂ = 15.

Pregunta 14. Si la mediana de los siguientes datos es 32,5, encuentra las frecuencias que faltan.

Intervalo de clases	0-10	10-20	20-30	30-40	40-50	50-60	60-70	Total
Frecuencia	F ₁	5	9	12	F ₂	3	2	40

Solución:

Media = 32,5 y N = 40

Intervalo de clases Frecuencia (f) cf

0-10 F ₁ F ₁

10-20 5 5 + f ₁

20-30 9 14 + f ₁

30-40 12 26 + f ₁

40-50 F ₂ 26 + f ₁ + f ₂

50-60 3 29 + f ₁ + f ₂

60-70 2 31 + f ₁ + f ₂

40

Ahora sabemos,

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ 32.5 = 30 + \frac{\frac{40}{2}-(14+f_1)}{12} * 10 \\ 32.5 - 30 = \frac{20-14-f_1}{12} *10 \\ 2.5 = \frac{6-f_1}{12}*10$

Resolviendo, obtenemos,

⇒ 2,5 x 12 = 60 – 10f ₁

⇒ 30 = 60 – 10f ₁

⇒ 10f ₁ = 60-30 = 30

⇒ f1 = 30/10 = ₃

∴ F ₂ = 9 – F ₁ = 9-3 = 6

Por lo tanto, f ₁ = 3, f ₂ = 6

Pregunta 15. Calcule la mediana para cada uno de los siguientes datos:

(i)

Marcas	Nº de alumnos	(ii) Marcas	Nº de alumnos
Menos de 10	0	Más de 150	0
menos de 30	10	Más de 140	12
Menos de 50	25	Más de 130	27
menos de 70	43	Más de 120	60
menos de 90	sesenta y cinco	Más de 110	105
Menos de 110	87	Mas que 100	124
Menos de 130	96	más de 90	141
Menos de 150	100	más de 80	150

Solución:

(i) Menos de

Marcas cf F

0-10 0 0

10-30 10 10

30-50 25 15

50-70 43 18

70-90 sesenta y cinco 22

90-110 87 22

110-130 96 9

130-150 100 4

Tenemos, N= 100

∴N/2 = 100/2 = 50 que se encuentra en el intervalo de clase perteneciente a 70-90 (∵ 50 < 65 y > 43)

∴ l = 70, F = 43 , f = 22 , h = 20

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 70 + \frac{50-43}{22} * 20 \\ = 70 + \frac{7 * 20}{22} \\ = 70 + \frac{70}{11} \\ = 76.36$

(ii) mayor que

Marcas cf F

Más de 150 (150-160) 0 0

140-150 12 12

130-140 27 15

120-130 60 35

110-120 105 45

100-110 124 19

90-100 141 17

80-90 150 9

Tenemos,

N = 150, N/2 = 150/2 = 75 que se encuentra en el intervalo de clase perteneciente a 110-120 (∵ 75 > 105 y 75 > 60)

∴ l = 110, F = 60 , f=45, h= 10

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ = 110 + \frac{70-60}{45} * 10 \\ = 110 + \frac{15}{45} * 10 \\ = 110 + \frac{10}{3} \\ = 113.33$

Pregunta 16. Se realizó una encuesta sobre la estatura (en cm) de 51 niñas de la clase X de una escuela y se obtuvieron los siguientes datos.

Altura en cm	numero de chicas
Menos de 140	4
Menos de 145	11
Menos de 150	29
Menos de 155	40
Menos de 160	46
Menos de 165	51

Encuentre la altura mediana.

Solución:

Altura (en cm) No de niñas (cf) F

135 – 140 4 4

140 – 145 11 7

145 – 150 29 18

150 – 155 40 11

155 – 160 46 6

160 – 165 51 5

51

Aquí, ∑F/2 = 51/2 = 25,5 o 26 que se encuentra en el intervalo de clase perteneciente a 145-150

Por lo tanto,

l= 145, F= 11, f= 18, h= 5

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ 145 + \frac{25.5-11}{18} * 5 \\ 145 + \frac{14.5}{18} * 5 \\ 145 + \frac{72.5}{18}$

= 145 + 4,03 = 149,03

Pregunta 17. Un agente de seguros de vida encontró los siguientes datos para la distribución de edades de 100 titulares de pólizas. Calcule la edad mediana, si las pólizas se otorgan solo a personas de 18 años en adelante pero menores de 60 años.

Edad en años	Número de asegurados
Por debajo de 20	2
Por debajo de 25	6
Por debajo de 30	24
Por debajo de 35	45
Por debajo de 40	78
Por debajo de 45	89
Por debajo de 50	92
Por debajo de 55	98
Por debajo de 60	100

Solución:

Edad en años
Nº de asegurados

(cf)
F

15-20 2 2

20-25 6 4

25-30 24 18

30-35 45 21

35-40 78 33

40-45 89 11

45-50 92 3

50-55 98 6

55-60 100 2

Total 100

Aquí N = 100, N/2 = 100/2 = 50 que se encuentra en el intervalo de clase de 35-40 ( ∵ 45 > 50 > 78)

Por lo tanto,

l = 35, F = 45, f = 33, h = 5

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ 35 + \frac{50-45}{33} * 5 \\ 35 + \frac{5}{33} * 5 \\ 35 + \frac{25}{33}$

= 35 + 0,76 = 35,76

Pregunta 18. Las longitudes de 40 hojas de una planta se miden con precisión al milímetro, y los datos obtenidos se representan en la siguiente tabla:

Longitud (en mm)	118-126	127-135	136-144	145-153	154-162	163-171	172-180
No de hojas	3	5	9	12	5	4	2

Encuentre la longitud media de la hoja.

Solución:

Longitud (en mm)

(en forma exclusiva)
Nº de hojas (f) cf

117,5 – 126,5 3 3

126,5 – 135,5 5 8

135,5 – 144,5 9 17

144,5 – 153,5 12 29

153,5 – 162,5 5 34

162,5 – 171,5 4 38

171,5 – 180,5 2 40

N = 40, N/2 = 40/2 = 20 que se encuentra en el intervalo de clase de 144,5-153,5 como 17 < 20 < 29

Por lo tanto,

l= 144,5, F= 17, f= 12, h = 9

$Median = l + \frac{\frac{N}{2}-F}{f} * h \\ 144.5 + \frac{20-17}{12} * 9 \\ 144.5 + \frac{3}{12} * 9 \\ 144.5 + \frac{9}{4}$

= 144,5 + 2,25 = 146,75

Pregunta 19. Una distribución incompleta se da de la siguiente manera:

Variable	0-10	10-20	20-30	30-40	40-50	50-60	60-70
Frecuencia	10	20	?	40	?	25	15

Te dan que el valor de la mediana es 35 y la suma de todas las frecuencias es 170. Usando la fórmula de la mediana, completa las frecuencias que faltan.

Solución:

Mediana = 25 y ∑f= N = 170

Supongamos que x e y son las dos frecuencias que faltan

Variable Frecuencia cf

0-10 10 10

10-20 20 30

20-30 X 30+x

30-40 40 70+x

40-50 y 70+x+y

50-60 25 95+x+y

60-70 15 110+x+y

∴ 110 + x + y = 170

⇒ x + y = 170 – 110 = 60

Aquí tenemos,

N = 170, N/2 = 170/2 = 85

Por lo tanto, Mediana = 35 que se encuentra en el intervalo de clase perteneciente a 30-40

Aquí l = 30, f = 40, F = 30 + x y h = 10

$Median = l + \frac{\frac{n}{2}-F}{f} * h \\ 35 = 30 + \frac{85-(30+x)}{40} * 10 \\ 35 - 30 = \frac{85-30-x}{4} \\ 5 = \frac{55-x}{4}$

20 = 55 – x

⇒ x = 55 – 20 = 35

Pero,

x + y = 60

Resolviendo para y, obtenemos,

∴ y = 60 – x = 60 – 35 = 25

Por lo tanto, las frecuencias perdidas x e y son 35 y 25.

Pregunta 20. La mediana de la distribución dada a continuación es 14.4. Encuentre los valores de x e y, si la frecuencia total es 20.

Intervalo de clases	0-6	6-12	12-18	18-24	24-30
Frecuencia	4	X	5	y	1

Solución:

Intervalo de clases Frecuencia Frecuencia acumulada

0-6 4 4

6-12 X 4+x

12-18 5 9+x

18-24 y 9+x+y

24-30 1 10+x+y

Sabemos, n = 20

Por lo tanto,

10 + x + y – 20,

=> x+y= 10 …(yo)

También,

Mediana = 14,4 que se encuentra en el intervalo de clase perteneciente a 12-18

Entonces, l = 12, f = 5, cf = 4 + x, h = 6

$Median = l + \frac{\frac{n}{2}-cf}{f} * h \\ 14.4 = 12 + \frac{10-(4+x)}{5} * 6 \\ 14.4 = 12 + (\frac{6-x}{5})*6$

Resolviendo para x, obtenemos,

x = 6 ….(ii)

También,

y = 6

Pregunta 21. La mediana de los siguientes datos es SO. Encuentre los valores de p y q, si la suma de todas las frecuencias es 90.

Marcas:	20-30	30-40	40-50	50-60	60-70	70-80	80-90
Frecuencia:	pags	15	25	20	q	8	10

Solución:

Marcas Frecuencia Frecuencia acumulada

20-30 pags pags

30-40 15 15 + p

40-50 25 40 + p = cf

50-60 20 = f 60 + pag

60-70 q 60 + p + q

70-80 8 68 + p + q

80-90 10 78 + p + q

Dado, N = 90

Y, N/2 = 90/2 = 45 que se encuentra en el intervalo de clase 50-60

Ahora,

Límite inferior, l = 50, f= 20, cf= 40 + p, h = 10

$Median = l + \frac{\frac{N}{2}-cf}{f} * h \\ = 50 + \frac{45-40-p}{20} * 10 \\ 50 = 50 + (\frac{5-p}{2}) \\ 0 = \frac{5-p}{2}$

Obteniendo valores, obtenemos,

∴ PAG = 5

Además, 78 +p + q = 90

⇒ 78 + 5 + q = 90

⇒ q = 90-83

∴ q = 7

Publicación traducida automáticamente

Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Solución Clase 10 RD Sharma – Capítulo 7 Estadísticas – Ejercicio 7.4 | conjunto 2

Pregunta 11. A continuación se da una distribución incompleta:

Se le da que el valor medio es 46 y el número total de elementos es 230.

Pregunta 12. Si la mediana de la siguiente distribución de frecuencias es 28,5, encuentre las frecuencias que faltan:

Pregunta 13. La mediana de los siguientes datos es 525. Encuentra la frecuencia que falta, si se da que hay 100 observaciones en los datos:

Pregunta 14. Si la mediana de los siguientes datos es 32,5, encuentra las frecuencias que faltan.

Pregunta 15. Calcule la mediana para cada uno de los siguientes datos:

Pregunta 16. Se realizó una encuesta sobre la estatura (en cm) de 51 niñas de la clase X de una escuela y se obtuvieron los siguientes datos.

Encuentre la altura mediana.

Pregunta 17. Un agente de seguros de vida encontró los siguientes datos para la distribución de edades de 100 titulares de pólizas. Calcule la edad mediana, si las pólizas se otorgan solo a personas de 18 años en adelante pero menores de 60 años.

Pregunta 18. Las longitudes de 40 hojas de una planta se miden con precisión al milímetro, y los datos obtenidos se representan en la siguiente tabla:

Encuentre la longitud media de la hoja.

Pregunta 19. Una distribución incompleta se da de la siguiente manera:

Te dan que el valor de la mediana es 35 y la suma de todas las frecuencias es 170. Usando la fórmula de la mediana, completa las frecuencias que faltan.

Pregunta 20. La mediana de la distribución dada a continuación es 14.4. Encuentre los valores de x e y, si la frecuencia total es 20.

Pregunta 21. La mediana de los siguientes datos es SO. Encuentre los valores de p y q, si la suma de todas las frecuencias es 90.

Deja una respuesta Cancelar la respuesta