Pregunta 1. Sin realizar realmente la división larga, indique si los siguientes números racionales tendrán una expansión decimal terminal o una expansión decimal periódica no terminal.
(i)23/8
Solución:
Denominador = 8
⇒ 8 = 2 3 x 5
El denominador 8 de la fracción 23/8 es de la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, 23/8 tiene una expansión decimal terminal que termina después de tres lugares decimales.
(ii) 125/441
Solución:
Denominador = 441.
⇒ 441 = 3 2 x 7 2
El denominador 441 de 125/441 no tiene la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, la fracción 125/441 tiene una expansión decimal periódica que no termina.
(iii) 35/50
Solución:
Denominador = 50.
⇒ 50 = 2×5 2
El denominador 50 de la fracción 35/50 es de la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, 35/50 tiene una expansión decimal terminal que termina después de dos decimales.
(iv) 77/210
Solución:
Denominador = 210.
⇒ 210 = 2x3x5x7
El denominador 210 de la fracción 77/210 no es de la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, 77/210 tiene una expansión decimal periódica que no termina.
(v) 129/(2 2 x 5 7 x 7 17 )
Solución:
El denominador = 2 2 x 5 7 x 7 17 .
El denominador de la fracción no se puede expresar en la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, 125/441 tiene una expansión decimal periódica que no termina.
(vi) 987/10500
Solución:
Al reducir la fracción anterior, tenemos,
987/10500 = 47/500 (forma reducida)
Denominador = 500.
⇒ 500 = 2 2 x 5 3
El denominador 500 de 47/500 se puede expresar en la forma 2 m x 5 n , donde m, n son números enteros no negativos.
Por lo tanto, 987/10500 tiene una expansión decimal terminal que termina después de tres lugares decimales.
Pregunta 2. Escriba las expansiones decimales de los siguientes números racionales escribiendo sus denominadores en la forma de 2m x 5n, donde myn son los números enteros no negativos.
(yo) 3/8
Solución:
El número racional es 3/8.
Podemos ver que 8 = 2 3 es de la forma 2 m x 5 n , donde m = 3 y n = 0.
Por lo tanto, el número dado tiene una expansión decimal terminal.
(ii) 13/125
Solución:
Podemos ver que 125 = 5 3 es de la forma 2 m x 5 n , donde m = 0 y n = 3.
Por lo tanto, el número racional dado tiene una expansión decimal terminal.
∴ 13/ 125 = (13 x 2 3 )/(125 x 2 3 )
= 104/1000
= 0,104
(iii) 7/80
Solución:
Podemos ver, 80 = 2 4 x 5 es de la forma 2 m x 5 n , donde m = 4 y n = 1.
Por lo tanto, el número dado tiene una expansión decimal terminal.
∴ 7/ 80 = (7 x 5 3 )/ (2 4 x 5 x 5 3 )
= 7 x 125 / (5 x 2) 4
= 875/10000
= 0.0875
(iv) 14588/625
Solución:
Podemos ver, 625 = 5 4 es de la forma 2 m x 5 n donde m = 0 y n = 4.
Entonces, el número dado tiene una expansión decimal terminal.
∴ 14588/ 625 = (14588 x 2 4 )/ (2 4 x 5 4 ) = 233408/10 4
= 233408/10000 = 23,3408
(v) 129/(2 2 x 5 7 )
Solución:
Podemos ver, 2 2 x 5 7 es de la forma 2 m x 5 n , donde m = 2 y n = 7.
Entonces, el número dado tiene una expansión decimal terminal.
∴ 129/ 2 2 x 5 7 = 129 x 2 5 / 2 2 x 5 7 x 2 5
= 4182/10 7
=4182/10000000
=0.0004182
Pregunta 3. Escribe el denominador del número racional 257/5000 en la forma 2m × 5n, donde m, n son números enteros no negativos. Por lo tanto, escribe la expansión decimal, sin división real.
Solución:
Denominador = 5000.
⇒ 5000 = 2 3 x 5 4
Se ve que, 2 3 x 5 4 es de la forma 2 m x 5 n , donde m = 3 y n = 4.
∴ 257/5000 = (257 x 2)/(5000 x 2) = 514/10000 = 0,0514 es la expansión decimal requerida.
Pregunta 4. ¿Qué puedes decir sobre la descomposición en factores primos de los denominadores del siguiente racional:
(yo) 43.123456789
Solución:
El número 43.123456789 tiene una expansión decimal terminal. Por lo tanto, su denominador es de la forma 2 m x 5 n , donde m, n son números enteros no negativos.
(ii)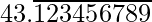 
[Tex] [/Tex]
Solución:
El racional dado tiene una expansión decimal no terminante. Por lo tanto, el denominador del número tiene factores distintos a los números 2 o 5.
(iii) 27.\overline{142857}
*** QuickLaTeX no puede compilar la fórmula:
*** Mensaje de error:
Error: nada que mostrar, la fórmula está vacía
Solución:
El número racional dado tiene una expansión decimal no terminante. Por lo tanto, el denominador del número tiene factores distintos de 2 o 5.
(iv) 0,120120012000120000….
Solución:
Desde 0.120120012000120000…. tiene una expansión decimal no terminante. Por lo tanto, el denominador del número tiene factores distintos de 2 o 5.
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA